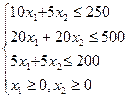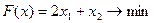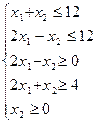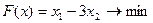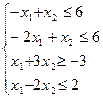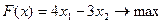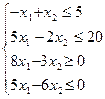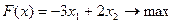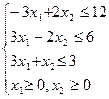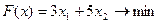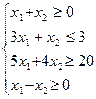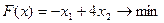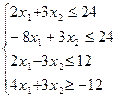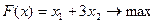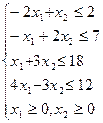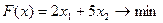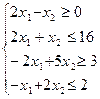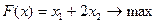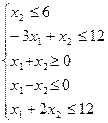Задачи линейного программирования

Линейное программирование  — это раздел математики, занимающийся решением таких задач на отыскание наибольших и наименьших значений, для которых методы математического анализа оказываются непригодными. Другими словами термин «линейное программирование» характеризует определение программы (плана) работы конкретного экономического объекта на основе выявления линейных связей между его элементами. Задачей линейного программирования является нахождение оптимального, т. е. наилучшего, плана при заданной системе налагаемых на решение ограничений.

К классу задач линейного программирования относится большое количество разнообразных задач планирования и управления, как, например:

1) нахождение оптимального плана выпуска продукции (оптимальное распределение ресурсов);

2) оптимизация межотраслевых потоков (планирование производства различных видов продукции по отраслям);

3) определение оптимального рациона (оптимизация состава химической смеси);

4) транспортная задача (оптимальное распределение потоков товарных поставок по транспортной сети);

5) задача о размещении производства (планирование с учётом затрат на производство и транспортировку продукции);

6) задача о назначениях (оптимальное распределение различных видов транспортных средств) и др.

Пример построения математической модели задачи

Предприятие изготавливает и продает краску двух видов: для внутренних и внешних работ. Для производства краски используется три исходных продукта S1, S2 и S3. Расходы продуктов и запасы этих продуктов на складе приведены в таблице:

 

Исходный продукт	Расход продуктов (в тоннах на 1 т. краски)		Запас продукта на складе (тонн)
	краска для внутренних работ	краска для внешних работ
S1	10	5	250
S2	20	20	500
S3	5	5	200

Выпуск 1 тонны краски для внутренних работ приносит предприятию прибыль в размере 200 денежных единиц (ден. ед.), для внешних работ - 200 ден. ед. Требуется определить, сколько краски каждого вида следует производить предприятию, чтобы получить максимальный доход (при соблюдении ограничений на ресурсы).

1) Введем переменные задачи:

Обозначим x ₁ - количество производимой краски для внутренних работ; x ₂ - соответствующее количество краски для наружных работ.

2)Ограничения, которым должны удовлетворять переменные задачи:

Учитывая количество каждого вида сырья для производства краски, а также запасы сырья и прибыль, получаемую от выпуска изделий, составим соответствующие ограничения.

3) Целевая функция задачи:

Обозначим Z доход от продажи краски, тогда целевая функция задачи записывается так:

Z = 200 х ₁ + 200 х ₂

 

Таким образом, задача состоит в том, чтобы найти максимум целевой функции

Z = 200 х ₁ + 200 х ₂  при ограничениях

Это и есть математическая модель задачи.

Практическое занятие №2

Наименование занятия: Решение задач линейного программирования графическим методом

Цель занятия: Научиться составлять математическую модель задачи линейного программирования, решать ее графическим методом. Формировать ОК 1 – ОК 9, овладеть знаниями и умениями, необходимыми для освоения ПК 1.1, ПК 1.2.

Подготовка к занятию: Повторить теоретический материал по теме «Линейное программирование»

Литература:

1. Лобачева М.Е. Конспект лекций «Математические методы», 2015г.

Перечень необходимых приборов, инструментов, материалов: ПЭВМ

Задание на занятие:

Задание 1. Решить задачу линейного программирования графическим методом

 

Вариант		Вариант
1		6
2		7
3		8
4		9
5		10

 

Задание 2. Составить математическую модель задачи и решить ее графическим методом

 

Один из цехов предприятия выпускает изделия двух видов: А и В. Для производства этих изделий требуются три вида сырья: S1, S2 и S3. На выпуск изделия А расходуется D1 кг S1, D2 кг S2 и D3 кг S3. На выпуск изделия В расходуется F1 кг S1, F2 кг S2 и F3 кг S3. Запасы ресурсов ограничены: за рабочую смену цех может израсходовать не более G1 кг S1, G2 кг S2 и G3 кг S3. Выпуск изделия А приносит предприятию прибыль в размере Р1 денежных единиц (ден. ед.), изделия В - Р2 ден. ед. Требуется составить оптимальный план работы цеха, т.е. найти, сколько изделий А и изделий В требуется выпускать, чтобы получить максимальную прибыль (при соблюдении ограничений на ресурсы).

 

Вариант	D1	D2	D3	F1	F2	F3	G1	G2	G3	P1	P2
1	5	10	20	20	5	5	500	250	200	300	100
2	15	10	10	10	10	10	400	200	350	150	250
3	10	15	10	10	15	5	200	400	350	250	150
4	15	15	5	15	5	15	450	250	250	200	200
5	10	20	5	5	20	5	250	500	200	200	200
6	5	15	15	15	5	15	250	250	450	200	200
7	5	15	15	15	15	5	250	400	250	200	200
8	10	15	10	15	10	10	300	300	250	250	150
9	15	10	10	10	10	15	300	250	300	250	150
10	10	10	15	10	15	10	250	300	300	150	250

 

Порядок проведения занятия:

1. Получить допуск к работе;
2. Выполнить задания в соответствии со своим вариантом;
3. Ответить на контрольные вопросы.

 

Содержание отчета:

1. Наименование, цель работы, задание;
2. Выполненное задание;
3. Выводы по результатам выполненного задания;
4. Ответы на контрольные вопросы.

 

Контрольные вопросы для зачета:

1. Какие задачи относятся к задачам линейного программирования?

2. Запишите общий вид задачи линейного программирования.

3. Геометрический метод решения задач линейного программирования, его достоинства и недостатки

4. Как определяется область допустимых решений?

5. Перечислите основные этапы решения задачи ЛПР графическим способом.

 

ПРИЛОЖЕНИЕ