Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Встроенные функции MathCAD для решения нелинейных алгебраических и трансцендентных уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнения в MathCAD решаются с помощью двух встроенных функцийroot и polyroots. 3.1.2.1 Встроенная функция MathCAD – root(F(x), x) Для численного решения уравнений предназначена стандартная функция MathCAD – root(F(x), x), которая возвращает значение корня с заданной точностью. Функция root имеет два аргумента: первый – выражение, стоящее в левой части уравнения, то есть F(x), второй – переменная, относительно которой решается уравнение, то есть x. Ищется значение переменной x, при которой выражение F(x) обращается в ноль. Функция root возвращает значение переменной x, которая обращает выражение F(x) в ноль. Второй аргумент - имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad пытается обратить выражение F(x) в ноль. Функция реализует вычисление итерационным методом и перед её применением необходимо задать начальное значение переменной x, принадлежащее интервалу изоляции корня. В зависимости от начального приближения функция root возвращает различные значения. Решение уравнений с помощью функции root может производиться с различной точностью, которая задается значением системной переменной TOL. Пример 3.1 Решить уравнение Процесс решения показан на рисунке 1. Выполняется следующая последовательность действий: 1.Сначала вводится функция 2. Задается точность. 3. Графически находится приближенное решение уравнения (можно использовать трассировку). 4. При помощи функции root выполняется нахождение решения уравнения с заданной точностью. 5. Выполняется проверка найденного решения. В зависимости от начального приближения функция root возвращает различные значения. Результат решения задачи приведён на рисунке 3.1.1 В результате найдены корни x0=-3.258, x1=0.2, x2=3.057.
Рисунок 3.1.1 – Пример решения нелинейного алгебраического уравнения
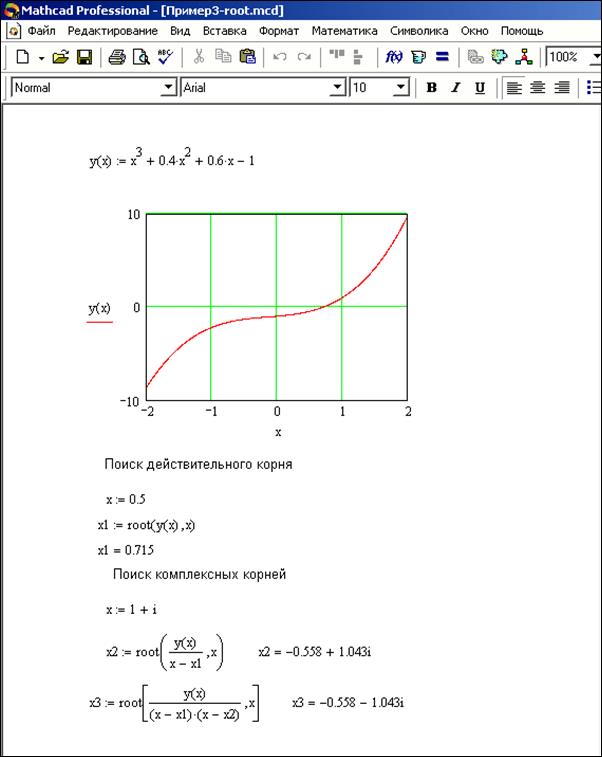
Функцию root можно записать в виде root (f(x), x, a, b), где a, b – пределы интервала изоляции корня. При такой форме записи нет необходимости задавать начальное значение х, так как оно определено в интервале Пример 3.2 Решить уравнение Результаты решения показаны на рисунке 2. Используя график функции, определяют пределы интервала изоляции каждого корня, а затем с помощью функции root (f(x), x, a, b) находят значение интересующего корня.
В данном случае найдено три корня. Необходимо правильно указывать интервал изоляции, в случае ошибки значение корня не будет найдено, что показано на рисунке 3.1.2
Рисунок 3.1.2 – Пример решения уравнения с использованием функции root (f(x), x, a, b)
На рисунке 3.1.3 показан пример решения уравнения, имеющего комплексные корни. В таких случаях начальное приближённое значение корня также должно быть комплексным. При вводе мнимого числа надо писать 1i, а не i. В данном примере при вычислении второго корня х2 первый исключается делением f(х) на (х-х1). При нахождении третьего корня f(х) делится на (х-х1)(х-х2).
Рисунок 3.1.3 – Пример решения уравнения, имеющего действительные и комплексные корни
Необходимо отметить особенность функции root, связанную с тем, что она не всегда позволяет найти значение корня. Mathcad при поиске корня с помощью функции root использует метод итераций. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным и функция root возвращает результат. Если после многих итераций Mathcad не может найти соответствующее приближение, то появляется сообщение об ошибке «отсутствует сходимость». Эта ошибка может быть вызвана следующими причинами: - уравнение не имеет корней; - корни уравнения располагаются далеко от начального приближения; - выражение имеет локальные максимумы или минимумы между начальным приближением и корнем; - выражение имеет разрывы между начальным приближением и корнями; - выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот). Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному решению.
|
|||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 6747; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.222.170 (0.01 с.) |

 с точностью
с точностью  .
.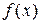 , соответствующая левой части уравнения.
, соответствующая левой части уравнения.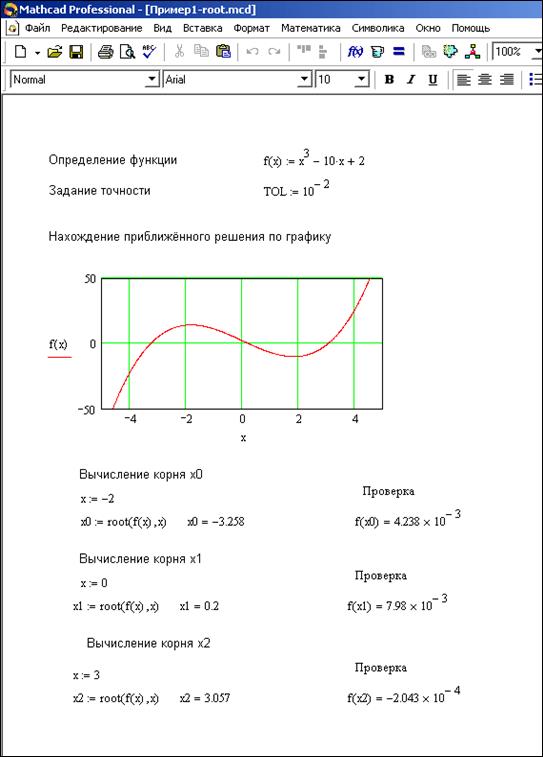
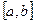 .
.