
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Встроенная функция MathCAD polyroots (v).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
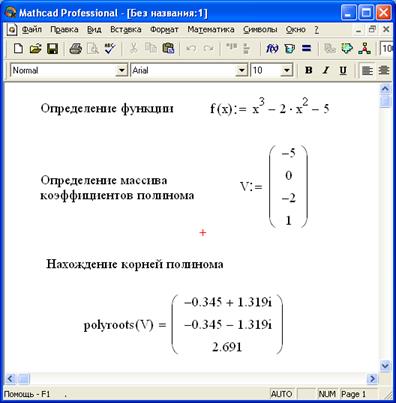
Для нахождения корней полинома в MathCAD предназначена специальная функция polyroots (v). Она находит как действительные, так и комплексные корни полинома n-ой степени, коэффициенты которого хранятся в массиве v длиной n+1. Параметром данной функции является вектор-столбец коэффициентов полинома v. Пример использования функции polyroots показан на рисунке 3.1.4. При решении задачи надо правильно формировать вектор-столбец коэффициентов полинома v, записывая в него значения коэффициентов, начиная коэффициентов при х в нулевой степени.
Решение систем уравнений
Системы уравнений в MathCAD решаются в следующем порядке: 1. Находится приближенное решение системы уравнений. Приближенное решение удобнее всего найти графически; 2. Записывается директива Given, и после нее записываются уравнения системы. Следует помнить, что вместо знака “равно” при записи уравнений используется знак “логическое равенство”, который набирается как <Ctrl>+<=>. 3. Записывается любое выражение, использующее функцию Find. Параметрами данной функции являются все переменные, входящие в систему. Функция возвращает вектор-столбец решений системы.
Рисунок 3.1.4 - Нахождение корней полинома при помощи функции polyroots
Пример 3.3 Найти решение системы уравнений
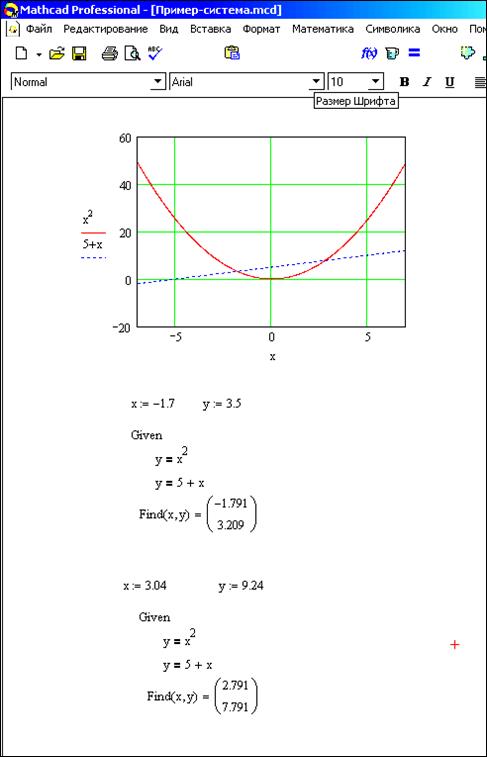
Процесс решения данной системы уравнений показан на рисунке 3.2.1 В результате функция Find вернула вектор-столбец
Символьное решение уравнений, неравенств и систем уравнений
Для символьного решения уравнений и неравенств надо выполнить следующее: 1. Вставить в рабочий лист структуру solve c панели инструментов Simbolic. 2. Ввести данные: слева – уравнение или неравенство, справа – переменную, относительно которой требуется его разрешить. 3. Щёлкнуть вне области решения, чтобы получить результат.
Рисунок 3.2.1 – Пример решения системы уравнений
При символьном решении уравнений и неравенств следует вводить знаки =, При символьном решении системы уравнений после Find надо ввести Пример символьного решения уравнений, неравенств и систем уравнений показан на рисунке 3.3.1
Рисунок 3.3.1 – пример символьного решения уравнения, неравенства и системы уравнений
Некоторые возможности MathCAD В этом разделе приводятся краткие сведения о возможностях MathCAD, которые могут быть полезны в процессе обучения. Комплексные числа в MathCAD MathCAD Воспринимает комплексные числа в форме a+bi, где a и b – вещественные числа. Комплексные числа можно вводить, или получать в результате вычислений. При вводе мнимые числа заканчиваются символом i или j. Нельзя использовать i или j сами по себе для обозначения мнимой единицы, во избежание смешения с именами переменных. Для ввода мнимой единицы следует напечатать 1i или 1j. При выходе из поля ввода единица не будет отображаться. Можно использовать j вместо i, если это удобнее. Чтобы MathCAD показывал нужный вам символ (i или j), выберите «Формат числа» из меню «Математика», нажмите на кнопку «Глобальный» и переключите «Мн.ед.» на i или j. MathCAD содержит следующие операторы и функции для работы с комплексными числами: Re(z) – вещественная часть z. Im(z) – мнимая часть z. arg(z) – угол в комплексной плоскости между вещественной осью и z. Результат заключён между π и –π.
При использовании в комплексной области многие функции являются многозначными. Для многозначной функции MathCAD возвращает значение, составляющее на комплексной плоскости самый малый положительный угол с положительным направлением действительной оси, то есть главное значение.
Рисунок 3.4.1 – Комплексные числа в MathCAD
На рисунке 3.4.1 показан пример использования возможностей MathCAD при работе с комплексными числами.
|
|||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 2701; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.126.27 (0.006 с.) |

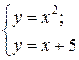 .
. и
и  . Это значит, что решением системы уравнений являются значения
. Это значит, что решением системы уравнений являются значения  и
и 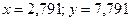 .
.
 , находящиеся на панели инструментов Boolean.
, находящиеся на панели инструментов Boolean. с панели инструментов Simbolic.
с панели инструментов Simbolic.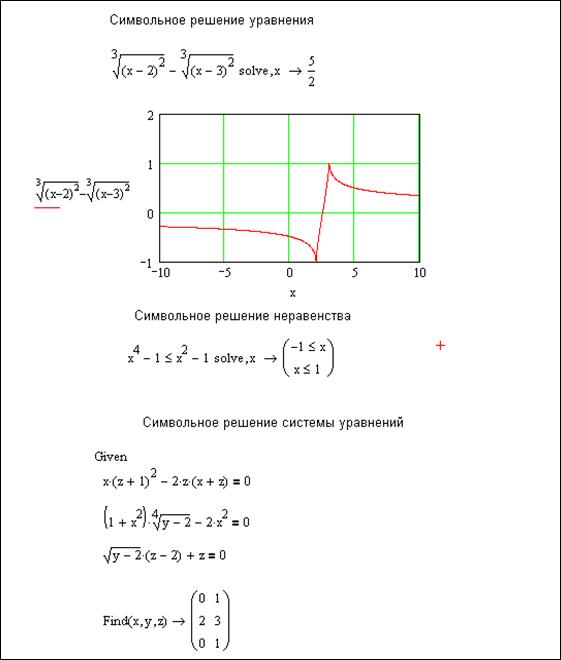
 - модуль z. Чтобы записать модуль выражения, заключите его в выделяющую рамку и нажмите клавишу с вертикальной чертой «|».
- модуль z. Чтобы записать модуль выражения, заключите его в выделяющую рамку и нажмите клавишу с вертикальной чертой «|».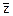 - Комплексно сопряжённое к z= a+bi, то есть a-bi. Чтобы применить к выражению этот оператор, выделите его и нажмите клавишу двойные кавычки «”».
- Комплексно сопряжённое к z= a+bi, то есть a-bi. Чтобы применить к выражению этот оператор, выделите его и нажмите клавишу двойные кавычки «”».



