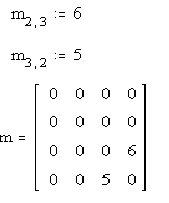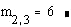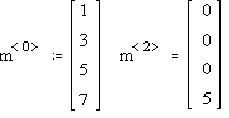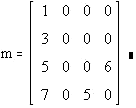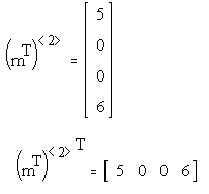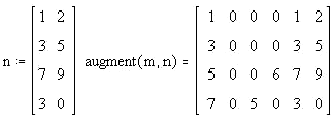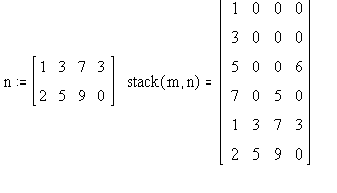Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение функции к выражениюСодержание книги
Поиск на нашем сайте
Чтобы сделать выражение аргументом функции, необходимо: · Заключить всё выражение в выделяющую рамку. · Нажать клавишу с одиночной кавычкой. · Нажать [Space]. Выделяющая рамка теперь охватит и скобки. · Нажать [Ins]. Срезанный уголок рамки будет слева. · Теперь напечатать имя функции. Если функция является встроенной, то можно выбрать пункт меню Вставить функцию из меню Математика и дважды щёлкнуть на имени функции. 2.4. Основные встроенные функции Чтобы посмотреть список всех встроенных функций в вашей версии MathCAD, выберите команду Вставить функцию из меню Математика.
2.5. Управление вычислениями Сразу после запуска MathCAD работает в Автоматическом режиме. Это означает, что MathCAD обновляет результаты в окне рабочего документа автоматически. Состояние автоматического режима отмечается словом ’’авто’’ в строке сообщений. Чтобы не терять времени на пересчёт рабочего документа при редактировании, можно отключить автоматический режим, выбрав пункт Автоматический режим из меню Математика или щёлкнув по кнопке с лампочкой на панели инструментов. Исчезают слово ’’авто’’ в строке сообщений и галочка около пункта Автоматический режим, указыва, что автоматический режим теперь выключен. Автоматическое обновление окна. То что MathCAD находится в автоматическом режиме означает, что: · Сразу после ввода знака равенства = MathCAD отображает результат вычислений. · Сразу после щелчка вне уравнения, содержащего знаки:= или ºº, MathCAD выполняет все вычисления, необходимые для правильного выполнения присваивания. При обработке определения после щелчка вне уравнения, его содержащего, в автоматическом режиме происходит следующее: · MathCAD вычисляет выражение - правую часть определения и присваивает результат имени, находящемуся в левой части определения. · Затем MathCAD находит в рабочем документе все другие уравнения, на которые влияет только что обработанное определение. · В заключение MathCAD обновляет затронутые обработанным определением уравнения, видимые в настоящий момент в окне рабочего документа. Хотя изменения в документе могут влиять на уравнения во всём рабочем документе, MathCAD выполняет только те вычисления, которые необходимы для обновления видимой в окне части, чтобы сэкономить время, затрачиваемое на обновление. При печати большого документа при переходе к его концу в автоматическом режиме MathCAD обновляет содержание рабочего документа целиком. Если MathCAD нуждается во времени для обновления, то указатель мыши изменяет свой вид, а в строке состояния появляется слово ’’ЖДИТЕ’’. Когда MathCAD вычисляет выражение, он отмечает его зелёным заштрихованным прямоугольником, что облегчает слежение за ходом вычислений. Чтобы заставить MathCAD вычислить все уранения на рабочем документе, выберите пункт Пересчитать всё из меню Математика. Ручное обновление окна. В ручном режиме MathCAD не вычисляет уравнения и не отображает результаты без специального запроса на вычисления, экономя таким образом время. При этом MathCAD следит за необходимостью отложенных вычислений. Сразу после внесения изменений, требующих вычислений, в строке сообщений появляется ’’Выч F9’’, напоминающее о том, что результаты видимые в окне, не соответствует текущему состоянию рабочего документа и нуждаются в пересчёте для обновления. Обновить окно можно либо выбрав пункт Пересчитать из меню Математика, либо нажав клавишу [F9], либо щёлкнув по кнопке со знаком равенства на панели инструментов.
Резюме В данном уроке были рассмотрены вопросы, связанные с вводом и редактированием выражений, определением переменных и их использованием, повторяющимися вычислениями и гибкость MathCAD’a в этом отношении, описаны основные встроенные функции и управление вычислениями. Урок 3. Визуализация расчётов в системе MathCAD. Построение графиков и диаграмм 3.1. Создание и редактирование графиков и диаграмм Создание пространства графика или диаграммы Для создания пространства графика (диаграммы)[1]: установите курсор в точку, которая станет левой верхней точкой пространства графика; выберите пункт Graph из меню Insert. В пункте Graph выберите вид графика (диаграммы). Всего существует 7 видов: 1. график в декартовой системе координат (подпункт меню X-Y Plot); 2. график в полярной системе координат (подпункт меню Polar Plot); 3. график в 3-мерной системе координат - поверхность вращения (подпункт меню Surface Plot); 4. график линий уровня (подпункт меню Contour Plot); 5. график в 3-мерной системе координат – поверхность интерполирования (3D Scatter Plot); 6. диаграмма в 3-мерной системе координат (подпункт 3D Bar Chart); 7. график векторного поля (подпункт Vector Field Plot). В результате выбора подпункта пункта Graph в пространстве листа MathCad’a будет выделена область пространства графика (см. Рис.1)
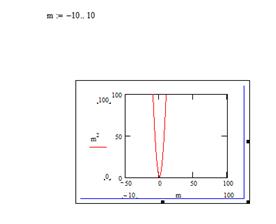
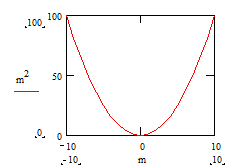
 Для задания функциональной зависимости, отображаемой на графике необходимо: 1. В позицию[2] под горизонтальной осью введите выражение, исходя из которого вы хотите построить график по оси Х. Например, наберите m, если вы ранее определили m как переменную интервала[3]. 2. В позицию рядом с вертикальной осью введите выражение, исходя из которого вы хотите построить график по оси Y. Например, наберите m2 для построения квадратичной функции от m. 3. Щёлкните мышью вне пространства графика. В результате будет получен график с по умолчанию формируемыми интервалами изменения значений аргумента и функции (см. Рис. 2).
На одном пространстве графика можно построить более одного графика.
Определение границ интервалов изменения значений аргумента и функции, отображаемых на графике Для определения границ интервалов щелчком мыши выделите пространство графика (диаграммы). Рядом с концами осей графика будут отображены 4 позиции (см. Рис. 3.а) при отсутствии заданной функциональной зависимости или 4 числа при заданной зависимости (см. Рис. 3.б), определяющие границы интервалов изменения аргумента и функции. Щёлкнув мышью на любом из них, вы получите возможность изменения его значения. Для окончания работы с графиком щёлкните вне пространства графика.

Простановка надписей на осях графика Двойным щелчком мыши по графику откройте диалоговое окно. Щёлкните мышью на вкладке Labels. В диалоговом окне Axis Labels введите надписи выбранных вами осей. Для отображения этих надписей на графике (диаграмме) включите соответствующие переключатели: X-Axis – для оси X, Y-Axis – для оси Y. Для подтверждения ввода нажмите “ОК”. Для отмены ввода нажмите “Отмена”. Добавление заголовка в график Щёлкните мышью на графике для открытия диалогового окна. Щёлкните мышью на вкладке Labels. В текстовом окне Title введите заголовок графика. Для вывода заголовка в верхней части графика (диаграммы) включите переключатель "Above", для вывода в нижней части – переключатель "Below". Для отображения заголовка на экране включите переключатель “Show Title”. Для подтверждения ввода нажмите “ОК”. Для отмены ввода нажмите “Отмена”.
Удаление пространства графика Щёлкните мышью на пространстве графика. С помощью этого вы выделите пространство графика квадратом. Нажмите Delete. График будет удалён.
Примеры построения графиков и диаграмм В предыдущих пунктах данного урока было детально объяснено, как построить график (диаграмму) в декартовой системе координат. В данном пункте урока будут приведены примеры построения всех 7 видов графиков и диаграмм. Построение всех графиков (диаграмм) аналогично вышеописанному и подробно повторяться больше не будет.
3.2. Построение графиков функций в декартовой системе координат Этот пример показывает, как построить хорошо форматированный график требуемой функции в декартовой системе координат.
Задайте функцию f(x), график которой вы хотите построить:
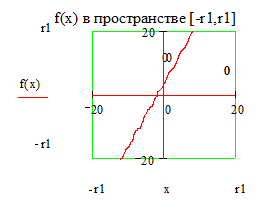
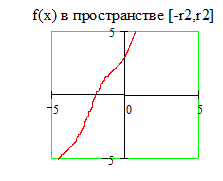
Границы графика: Замечание: В данном примере функция строится в пространстве -r1 x r1, -r1 y r1 и в пространстве -r2 x r2, -r2 y r2. Для создания пространства графика функции f(x) в пространстве с границами по умолчанию установите курсор в пространстве листа и наберите f(x)[Shift]@.
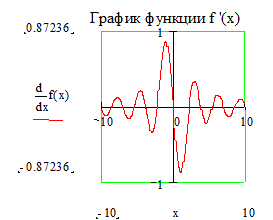
Быстрое построение графика функции и её производной в декартовой системе координат Этот пример показывает, как построить хорошо форматированный график требуемой функции и её производной в декартовой системе координат. Задайте функцию f(x), график которой вы хотите построить:
Для ввода оператора дифференцирования
Быстрое построение дискретно заданной функции в декартовой системе координат
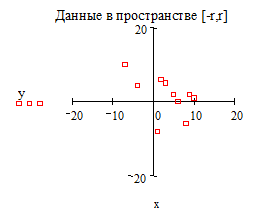
Этот пример показывает, как построить хорошо форматированный график дискретно заданной функции в декартовой системе координат. Задайте матрицу данных (координата X - в первом столбце, координата Y – во втором столбце):
Примечание: Для ввода оператора оператора взятия столбца матрицы Границы графика: Замечание: В данном примере функция строится в пространстве -r x r, -r y r. Для создания графика в пространстве, выбираемом MathCAD по умолчанию перейдите в рабочее пространство всего листа м наберите y@x[Enter].
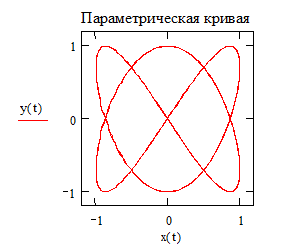
3.3. Построение кривых, заданных параметрически Этот пример показывает, как построить график кривой, координаты точек которой являются функциями одного параметра. Задайте x и y как функции одного параметра t:
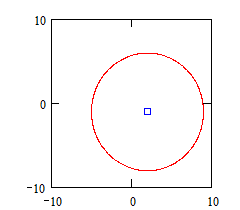
Построение графика окружности Этот пример может быть использован для построения графика окружности заданного радиуса, с заданными координатами центра. Задайте значение координаты x центра: Задайте значение координаты y центра: Задайте значение радиуса окружности: Границы графика:
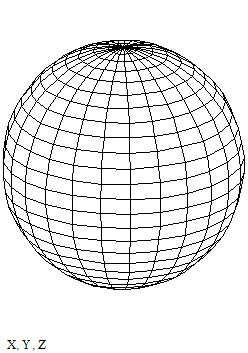
Построение сферы Этот пример может быть использован при построении графика параметрически заданной сферы. Задайте количество параллелей:
3.4. Построение поверхности вращения вокруг оси X
Этот пример может быть использован при построении поверхности вращения функции f(x) вокруг оси X.
Задайте функцию f(x):
Задайте верхнюю и нижнюю границы интервала изменения переменной x:
График функции f(x) на Поверхность вращения: заданном интервале:
3.5. Построение поверхности вращения вокруг оси Y Этот пример может быть использован при построении поверхности вращения функции f(x) вокруг оси X. Задайте функцию f(x): Задайте верхнюю и нижнюю границы интервала изменения переменной x:
График функции f(x) на Поверхность вращения: заданном интервале:
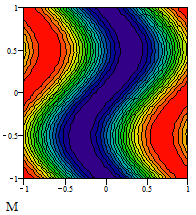
3.6. Построение линий уровня функции двух переменных Этот пример может быть использован при построении линий уровня как функции двух переменных. Задайте функцию двух переменных: Задайте границы интервала изменения переменной х: Задайте количество точек разбиения интервала изменения переменной х:
Задайте границы интервала изменения переменной y: Задайте количество точек разбиения интервала изменения переменной y:
Линии уровня:
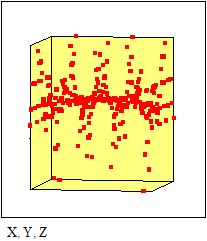
3.7. Быстрое построение трёхмерной интерполированной поверхности Этот пример может быть использован при построении трёхмерной проинтерполированной поверхности, как функции от двух переменных, заданной вами. Задайте функцию f(x,y), график которой вы хотите построить:
Задайте интервалы изменения переменных x и y: Примечание: В этом примере функция отображается в пространстве -xr x xr, -yr y yr. Задайте количество точек дискретизации: Программа нахождения отдельных точек поверхности:
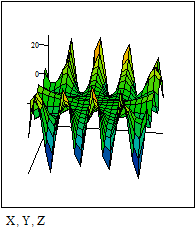
График трёхмерной дискретизированной График проинтерполированной поверхности: поверхности:
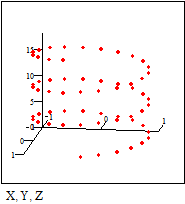
3.8. Быстрое построение кривой в трёхмерной системе координат Этот пример может быть использован при построении графика дискретной функции в системе координат X-Y-Z. Задайте количество точек дискретизации: Определите координаты точек по каждой из осей:
График трёхмерной дискретной функции:
Урок 4. Вектора, матрицы, переменные-диапазоны
4.1. Создание векторов и матриц <small> Для создания матрицы размером до ста элементов требуется выполнить следующие действия: Либо выберите пункт меню Matrix из меню Insert, для появления диалогового окна, с просьбой ввести высоту и ширину матрицы, либо на панели с основными компонентами нажмите кнопку <small>Примечание: при таком способе создания матрицы, возможен ввод не более 10 строк и столбцов, если требуется использовать большие размерности, то следуйте способам изложенным ниже. Примечание: нумерация строк и столбцов начинается с 0.<small></small></small> <small>Вектор задается, так же как и матрица, но количество колонок = 1. <big> Пример: </big>
<small>Следует учесть, что в данном примере использовались переменные-диапазоны, которые будут описаны в шестом пункте. <small>Примечание: для создания матрицы можно воспользоваться комбинацией горячих клавиш Ctrl-M</small>. <small> Существует возможность чтения матрицы данных из файла: Примечание: данные модифицируют автоматически в Mathcad всякий раз, когда изменяется файл данных.</small> <!--msimagelist--> 1. <small> Выберите из подменю Component из меню Insert </small> <!--msimagelist--><!--msimagelist--> 2. <small> Выберите Data File Read/Write из списка, и нажмите "Next". При этом запустится Wizard установки Data File Read/Write. </small> <!--msimagelist--><!--msimagelist--> 3. <small> Выберите " Read from data source " и нажмите "Next". </small> <!--msimagelist--><!--msimagelist--> 4. <small> Затем выберите путь к файлу, указав перед этим тип файла (по умолчанию – текстовый). </small> <!--msimagelist--><!--msimagelist--> 5. <small> Нажмите "Finish".
Пример:
<small> В результате переменная f содержит матрицу. Можно легко вставить матрицу чисел из Excel: </small> 1. <small> Выделите ячейки в Excel-е и скопируйте их в буфер. </small> <!--msimagelist--><!--msimagelist--> 2. <small> Перейдите в Mathcad и на рабочем листе создайте переменную, которая будет содержать матрицу. Введите знак “:=”. </small> <!--msimagelist--><!--msimagelist--> 3. <small> Вставьте матрицу из буфера. Матрицу можно задавать и поэлементно, например: </small> <!--msimagelist--><!--msimagelist-->
4.2. Извлечение элементов, строк и столбцов <small>Чтобы получить доступ к отдельному элементу необходимо набрать имя матрицы и задать индексы строки и столбца. Для легкости наберите после имени матрицы “[“, при этом нужно лишь задать индексы через запятую.</small> Пример:
<small> Для доступа к целому столбцу необходимо лишь набрать имя матрицы, затем “Ctrl-6” и ввести номер столбца. </small> Пример:
<small>Примечание: данная процедура может использоваться как для заполнения, так и для вывода содержимого матрицы на экран. </small> <small> <small></small> Теперь матрица будет иметь вид: </small>
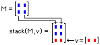
<small> Для доступа к строкам матрицы можно использовать операцию транспонирования. Для получения первого результата нужно набрать “m Ctrl-1 Ctrl-6 =”. А для получения строки в нормальном виде: “ m Ctrl-1 Ctrl-6 Ctrl-1 =”. </small> <small>Примечание: эта операция используется не для заполнения матрицы. </small> Пример:
4.3. <small> Изменение размеров матриц и векторов <small> Объединения двух матриц, либо матрицы и вектора можно провести двумя способами:
1. </small> <small>Присоединением к исходной матрице справа, для этого размерность исходной матрицы должна быть mx,n, присоединяемой матрицы mx,p, результирующая матрица будет иметь размерность mx,(n+p). Для этого используется функция </small><big>augment(A,B)</big><small>. Схематически это выглядит так.</small><!--msimagelist--><!--msimagelist-->
Пример:
<!--msimagelist--> 2. <small>Присоединением к исходной матрице снизу, для этого размерность исходной матрицы должна быть m x,n, присоединяемой матрицы p x,n, результирующая матрица будет иметь размерность (m+p) x, n. Для этого используется функция </small><big>stack(A,B)</big><small>. Схематически это выглядит так.</small><!--msimagelist--><!--msimagelist-->
Пример:
<small> В Mathcad существует возможность удалять и вставлять любое количество строк или столбцов из матрицы. Для этого: 1. <small> Выберите в матрице элемент той строки или столбца, который Вы собираетесь удалить. </small> <!--msimagelist--><!--msimagelist--> 2. <small> Нажмите “Ctrl-M” или выберите пункт меню Matrix из меню Insert, в результате в появившемся диалоговом окне выберите количество строк или столбцов которые вы собираетесь удалить. </small> <!--msimagelist--><!--msimagelist--> 3. <small> Нажмите кнопку Delete. </small> <!--msimagelist--><!--msimagelist--> 4. <small> Нажмите кнопку Close (Если нажать кнопку Ok, то ничего не изменится) </small> <!--msimagelist--><!--msimagelist--> <small> Для вставки строк или столбцов алгоритм примерно тот же, только нужно учесть, что вставляемая строка будет располагаться ниже выбранного элемента, а столбец – справа. Также в диалоговом окне следует выбрать кнопку Insert. </small>
<small> 4.4. Основные функции и операторы для работы с векторами и матрицами </small> <small> Mathcad имеет целый ряд функций для работы с матрицами и векторами. Для удобства объединим их по группам. </small> Объединение матриц: <big>augment(A,B) Разъединение матриц: <big>submatrix(A,ir,jr,ic,jc)</big> <small> Размер матрицы: <big>cols(A) </small><big>length(v) </small><big>identity(n)</big> <small> Функции экстремума: <big>max(A) <small> 4.5. Манипуляции с матрицами </small> <small> Следующие операции имеют специальное значение для векторов и матриц. Большинство этих операторов являются доступными из символьной палитры, но все имеют соответствующие горячие клавиши. <small> Примечание: операторы, которые используют вектора, всегда используют их как столбцы, а не как строки. </small>
<small><small> Примечание: все вышеперечисленные операции можно проводить и над матрицами в символьном виде.
<small></small></small> <small> 3.6. Переменные-диапазоны
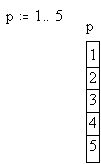
<small>Переменные-диапазоны – это переменные содержащие все значения в указанном промежутке, причем если не указана точность, то значения берутся целочисленные. Для того чтобы задать переменную-диапазон существует горячая клавиша “;”. Вид этих переменных следующий “..”.</small> Пример:
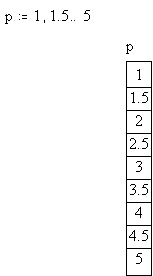
<small> Точность задается следующим образом: после нижней границы диапазона ставится точка, и за ней идет следующее значение, разность между ними и определяет точность итераций. </small> Пример:
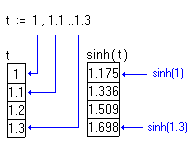
<small> Существует возможность вычисления функций от переменных-диапазонов, причем выдается ряд значений – значения функции в точках итерирования. </small> Пример: <small> </small> Урок 5
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.01 с.) |


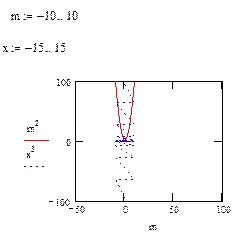
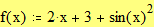
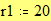
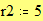
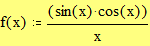
 наберите?.
наберите?.

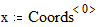
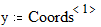
 наберите Ctrl+6.
наберите Ctrl+6.
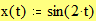
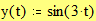
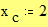

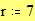

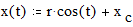

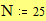
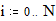
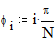
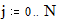
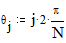
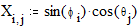
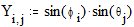

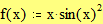
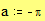

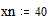
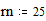
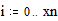
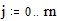
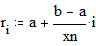
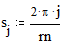
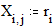
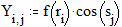


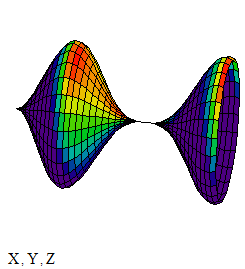


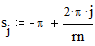
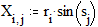
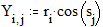
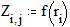



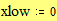


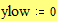
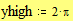
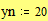
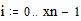
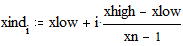
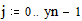
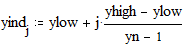
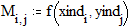
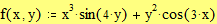
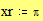

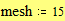
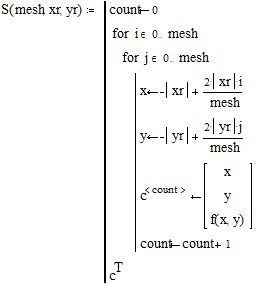
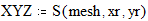






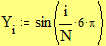
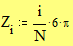
 </small><small>, а на появившейся панели кнопку
</small><small>, а на появившейся панели кнопку  </small><small>, в результате чего на экране появится то же диалоговое окно. </small>
</small><small>, в результате чего на экране появится то же диалоговое окно. </small>