
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая палитра (Math Palette)Содержание книги
Поиск на нашем сайте
Меню Подобно другим программам под Windows, MathCAD содержит полосу меню. С помощью меню пользователю доступны все команды программы. Математическая палитра (Math Palette) Математическая палитра (Рис.1.2) предназначена для получения доступа к палитрам MathCAD’а.
Рис. 1.2. Math Palette. Каждая кнопка математической палитры, открывает палитру символов. Эти палитры служат для вставки операторов, греческих букв, графиков и т.д. Опишем назначение каждой из них.
Панель инструментов Панель инструментов MathCAD показана на рисунке 1.3. Многие команды меню можно быстро вызывать, нажав кнопку на панели инструментов. Для того, чтобы узнать, что делает кнопка, установите на нее указатель мыши, после чего на экране появится подсказка, описывающая действие кнопки.
Рис. 1.3. Панель инструментов MathCAD.
Панель редактирования На рисунке 1.4 представлена панель редактирования MathCAD. Она содержит шаблоны выбора и кнопки, используемые для задания характеристик текста в уравнениях и текстовых блоках.
Рис. 1.4. Панель редактирования MathCAD.
1.3. Ввод выражений Для ввода выражений в рабочий документ MathCAD можно использовать как клавиатуру, так и мышь. При вводе с клавиатуры используются как отдельные клавиши, так и их комбинации. Опишем основные применяемые в MathCAD комбинации клавиш, используемые для ввода выражений.
Для ввода произвольного текста в рабочий документ MathCAD, в программе предусмотрена возможность вставки текстовых областей. Для этого необходимо активизировать подпункт [Text Region] меню [Insert], либо нажать клавишу ["].
Пример: При нажатии следующей последовательности клавиш: [\], [1], [-], [Ctrl]+[P], [/], [7], в рабочий документ MathCAD вводится приведенное ниже выражение.
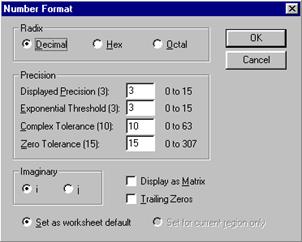
1.4. Настройка параметров программы При выполнении математических вычислений очень часто возникает вопрос формата вывода результата. MathCAD позволяет устанавливать формат вывода чисел: 1. задавать количество знаков, в дробной части десятичного числа; 2. задавать вид числа: десятичный, экспоненциальный. Выбрав пункт [Number...] из меню [Format], пользователь получает доступ к диалоговому окну, изображенному на рис. 1.5.
Рис. 1.5. Диалоговое окно настройки формата чисел
Опции этого окна позволяют установить число десятичных знаков в выводимых числах, границы использования экспоненциального представления чисел, систему счисления: десятичную, восьмеричную или шестнадцатеричную и формат отображения комплексных чисел. Кроме вышеперечисленных параметров, MathCAD имеет встроенные переменные, отвечающие за формат выводимых чисел. Перечислим их.
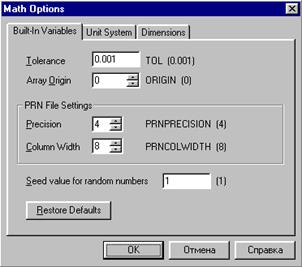
Для настройки значений этих переменных можно использовать операции присвоения, о чем будет изложено в последующих уроках, либо воспользоваться диалоговым окном, вид которого изображен на рисунке 1.6.
Рис. 1.6. Диалоговое окно математических настроек
Данное диалоговое окно активизируется с помощью пункта [Options...] меню [Math]. С его помощью осуществляется также настройка параметров размерностей (units). При изменении формата вывода результата меняется только их внешний вид. Внутреннее представление чисел в MathCAD всегда имеет полную точность.
1.5. Погрешности вычислений Большинство вычислений в системе реализовано с помощью численных методов, принципиально имеющих погрешность вычислений. Так, для вычислений производной используется конечно-разностный метод с изменением шага между узлами и его подстройкой под заданную погрешность. Интегралы вычисляются методом Ромберга с заданной погрешностью, а для вычисления корней функций применяется метод секущих.
Для всех методов погрешность вычислений задается с помощью специальной системной переменной TOL. Хотя истинная погрешность может оказаться заметно меньше значения TOL, ее влияние на результаты вычислений заметно на рисунке.
Резюме В уроке 1 рассмотрены основы интегрированной среды системы MathCAD и её характерные черты, описаны основные панели инструментов, порядок ввода выражений, порядок настройки формата отображаемых на экране чисел, вопрос точности вычислений. Урок 2. Вычисления, символьный процессор, работа с использованием встроенных и пользовательских функций 2.1. Ввод и редактирование выражений Формулы в MathCAD могут размещаться в любом месте рабочего документа. Чтобы подвести курсор к нужному месту, невидимому в настоящий момент времени в окне, можно использовать полосы прокрутки, как в любой программе под Windows. Каждая кнопка в полосе, находящейся ниже меню, открывает палитру символов. Эти палитры служат для вставки 1) общих арифметических операторов; 2) знака равенства и знаков отношений; 3) различных двух- и трёхмерных графиков; 4) матричных и векторных операторов; 5) производных, интегралов и пределов. Рядов и произведений; 6) программных структур; 7) греческих букв.
Хотя MathCAD предназначен для сложных математических вычислений, его легко можно использовать как простой калькулятор. Например: · После щелчка в любом месте рабочего документа появляется небольшой крестик, теперь всё введённое с клавиатуры будет размещаться начиная с места расположения крестика
· Напечатайте 15-8/104.5= · После набора знака = MathCAD вычисляет выражение и выводит результат.
Выражение на экране можно редактировать, устанавливая в нужном месте указатель и печатая новые символы, цифры или операторы. Многие операторы и греческие буквы могут быть в том числе напечатаны и с помощью палитры символов, расположенной под полосой меню. Ключевым шагом в редактировании выражений в MathCAD является заключение подходящей части выражения в выделяющую рамку. Поэтому стоит запомнить правило: · То, что заключено в выделенную рамку, становится операндом следующего вводимого оператора. По отношению к редактированию уравнений знание правил использования выделяющей рамки может сравниться с пониманием назначения маркера ввода текста, который используется в большинстве текстовых процессоров. В текстовом редакторе маркер ввода текста имеет вид вертикальной полоски, потому что текст, по сути, одномерен. Новые символы могут идти либо влево, либо вправо от старых. Формулы же, скорее, имеют двумерную, древовидную структуру. Поэтому MathCAD использует двумерную разновидность маркера ввода, а именно выделяющую рамку.
Допустим, например, что надо напечатать немного более сложное выражение
· Напечатайте x-3*a^2. До сих пор правила старшинства позволяли нам просто печатать символы подряд, дальше так продолжать нельзя, поскольку маркер ввода находится на 2, только 2 станет если нажать /. Так как нужно чтобы выражение x-3*a^2 целиком стало числителем, следует использовать выделяющую рамку.
· Чтобы заключить x-3*a^2 в выделяющую рамку, нажмите [Space]. Маркер ввода превратится в выделяющую рамку. Нажмите [Space] ещё три раз, чтобы рамка охватила выражение целиком. · Нажмите /, чтобы создать дробную черту. · Теперь напечатайте -4+ и щёлкните на кнопке, помеченной Цепкие операторы Операции деления, возведения в степень и извлечения корня являются в MathCAD “цепкими” операциями. Это означает, сто после создания одной из этих операций, всё затем вводимое будет частью знаменателя, показателя степени или подкоренного выражения, пока явно не переместить курсор, нажимая [Space] или с помощью мыши. 2.2. Определения и переменные Гибкость и мощь MathCAD становятся ясными при использовании переменных и функций. При помощи переменных и функций становятся возможными связь уравнений и использование промежуточных результатов в дальнейших вычислениях. Следующие примеры показывают, как определять и использовать переменные. Определение переменных. Имена в MathCAD могут содержать любые из следующих символов: · Прописные и строчные латинские буквы. · Цифры от 0 до 9. · Знак подчёркивания(_). · Штрих (`). Обратите внимание, что это не тоже самое что апостроф. Этот символ находится на одной клавише с тильдой (~). · Символ процента(%). · Греческие буквы. Чтобы вставить греческую букву напечатайте соответствующую латинскую букву и нажмите [Ctrl]+[G]. · Символ бесконечности Имена функций и переменных не могут включать пробелы или любые иные символы, не перечисленные выше. К именам переменных относятся следующие ограничения: · Имя не может начинаться с цифры, знака подчёркивания (_), штриха (`), или символа процента (%). · Символ бесконечности
· Любые символы, напечатанные после нажатия клавиши точки (.), будут записаны как нижний индекс. · Все символы в имени должны быть напечатаны шрифтом одной гарнитуры, размера и начертания (курсив, полужирный и т.д.). Это ограничение не накладывает ограничений на появление в любом имени греческих букв. · MathCAD не делает различий между именами переменных и именами функций. Т.о. если определить вначале f(x), а затем переменную f, окажется невозможным использовать f(x) где-либо ниже определения f. · Некоторые имена уже используются MathCAD для построенных констант, единиц измерения и функций. Хотя эти имена можно переопределить, имейте ввиду, что это уничтожит их встроенные значения. Например, если определить переменную mean, встроенная функция MathCAD mean(v) не сможет больше использоваться. Для того, чтобы определить t нужно: · Ввести t: (символ t сопровождается двоеточием). MathCAD показывает двоеточие сопровождаемое символом присваивания:= · Напечатать, например, 10 в пустом поле, чтобы завершить определение t. Если при вводе была допущена ошибка, нужно выделить выражение мышью и нажимать клавишу [Space] до тех пор, пока выделяющая рамка не окружит всё выражение. Затем его можно удалить использовав пункт Вырезать из меню Правка. Таким образом чтобы определить любую переменную, необходимо: · Напечатать имя переменной, которую необходимо определить · Напечатать двоеточие, чтобы ввести символ определения. · Напечатать значение присваиваемое переменной. Значение может быть одиночным числом, как в вышеприведённом примере, или более сложным сочетанием чисел и ранее приведённых переменных. MathCAD читает рабочий документ сверху вниз и слева направо. Определив переменную, например t, её можно использовать в вычислениях везде ниже и правее равенства, которым она определена. Вычисления результатов
Теперь когда переменные определены, например пускай это будут acc и t, их значения могут быть использованы в других выражениях. · Поместите указатель мыши на несколько строк ниже двух предыдущих определений · Напечатайте, например, acc/2 [Space] * t^2. Символ крышка(^) означает возведение в степень, звёздочка (*) - умножение, а наклонная черта вправо(/) - деление. · Нажмите знак =.
После ввода формулы MathCAD возвращает результат так как это показано на рисунке. Окно теперь содержит два определения, которые определяют переменные, и одно вычисление, которое даёт результат. Комплексные числа MathCAD воспринимает комплексные числа в форме a+bi, где а и b - обычные числа. Можно использовать букву j вместо i если это удобнее. Комплексные числа могут также возникать в результате вычислений, даже если все исходные значения вещественны. Например, если вычислить При вводе комплексных чисел не забудьте, что нельзя использовать i или j сами по себе для ввода комплексной единицы. Нужно всегда печатать 1i или 1j, в противном случае MathCAD истолкует i или j как переменную. В MathCAD есть следующие специальные функции и операторы для работы с комплексными числами:
2.3. Повторяющиеся вычисления
MathCAD может выполнять повторяющиеся или итерационные вычисления так же легко, как вычисления отдельных выражений. С этой целью MathCAD использует специальный тип переменных - дискретные аргументы. Переменная типа дискретный аргумент принимает диапазон значений, например, все целые числа от 0 до 10. Если в выражении присутствует дискретный аргумент, MathCAD вычисляет выражение столько раз, сколько значений содержит дискретный аргумент. Описание дискретного аргумента Для того чтобы вычислить выражение для диапазона значений, сначала определите дискретный аргумент. Например, надо вычислить результаты для диапазона значений t от 10 до 20 с шагом 1. Это делается таким образом:
· Сначала нужно отредактировать определение t, чтобы сделать её дискретным аргументом. Для этого нужно щёлкнуть мышкой на 10 в равенстве t=10. Указатель ввода должен появится вслед за 10, как показано на рисунке.
· Напечатайте,11. Это действие определяет следующее число в диапазоне как 11.
· Напечатайте;20; чтобы определить последнее число в диапазоне как 20. MathCAD изображает символ точки с запятой, как два символа точки подряд.
· После щелчка мышью вне равенства для t MathCAD вычисляет его для всех значений t, входящих в диапазон. Так как t содержит в нашем случае одиннадцать различных значений, то получается одиннадцать различных ответов. Они отображаются в таблице, как показано на рисунке.
Определение функции Ещё большей гибкости вычислений можно достичь, используя определения функций. Приведём пример:
· Начните определение функции d(t), напечатав d(t):
· Завершите определение, напечатав выражение 1600+acc/2 [Space] *t^2 [Enter] Определение функции завершено. Имя функции - d, аргумент функции - t. Можно использовать эту функцию, чтобы вычислить значение выражения - её правой части - для произвольных значений t. Для этого нужно подставить вместо t соответствующее число. Например:
· Чтобы вычислить значение для значения 12,5 достаточно напечатать d(12.5)=. MathCAD возвратит соответствующее значение, как показано на рисунке.
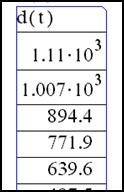
· Чтобы вычислить функцию для каждого значения t из диапазона, определённого ранее, достаточно щёлкнуть мышью внизу других уравнений и ввести d(t)=. MathCAD выведет таблицу значений. Первые два из них записаны в экспоненциальном виде. Формирование результата MathCAD может устанавливать формат вывода чисел, т.е. изменять число выводимых десятичных знаков, менять экспоненциальный вид представления чисел на обычную запись с десятичной точкой и так далее. Например, можно изменить таблицу с предыдущего рисунка так, чтобы ни одно из чисел не имело экспоненциального представления:
· Щёлкните мышью на таблице, выделив её, как показано на рисунке. · Выбрав пункт меню Формат Числа из меню Математика, откройте диалоговое окно “Формат Числа”. Опции этого окна позволяют установить количество десятичных знаков в выводимых числах, границы использования экспоненциального представления чисел и систему счисления: десятичную, восьмеричную, шестнадцатеричную. Кнопка выбора “Локальный” должна быть отмечена, чтобы установки в этом диалоговом окне воздействовали только на выбранную часть рабочего документа. · Значение по умолчанию для “Диапазона показателя” - 3. Это означает, что только числа большие или равные 103, отображаются в экспоненциальном представлении. Чтобы заменить 3 на 6, например, нужно щёлкнуть мышью справа от 3, нажать [BkSp] и напечатать 6.
· Нажмите на кнопку “OK”. Результаты в таблице изменятся соответственно новому формату - 1110 больше не имеет экспоненциального представления. При изменении формата вывода результатов меняется только их внешний вид. Внутреннее представление чисел MathCAD всегда имеет полную точность. Резюме В данном уроке были рассмотрены вопросы, связанные с вводом и редактированием выражений, определением переменных и их использованием, повторяющимися вычислениями и гибкость MathCAD’a в этом отношении, описаны основные встроенные функции и управление вычислениями. Урок 3. Визуализация расчётов в системе MathCAD. Построение графиков и диаграмм 3.1. Создание и редактирование графиков и диаграмм Создание пространства графика или диаграммы Для создания пространства графика (диаграммы)[1]: установите курсор в точку, которая станет левой верхней точкой пространства графика; выберите пункт Graph из меню Insert. В пункте Graph выберите вид графика (диаграммы). Всего существует 7 видов: 1. график в декартовой системе координат (подпункт меню X-Y Plot); 2. график в полярной системе координат (подпункт меню Polar Plot); 3. график в 3-мерной системе координат - поверхность вращения (подпункт меню Surface Plot); 4. график линий уровня (подпункт меню Contour Plot); 5. график в 3-мерной системе координат – поверхность интерполирования (3D Scatter Plot); 6. диаграмма в 3-мерной системе координат (подпункт 3D Bar Chart); 7. график векторного поля (подпункт Vector Field Plot). В результате выбора подпункта пункта Graph в пространстве листа MathCad’a будет выделена область пространства графика (см. Рис.1)
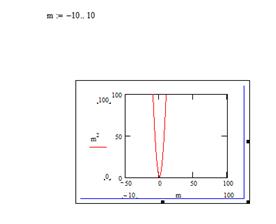
 Для задания функциональной зависимости, отображаемой на графике необходимо: 1. В позицию[2] под горизонтальной осью введите выражение, исходя из которого вы хотите построить график по оси Х. Например, наберите m, если вы ранее определили m как переменную интервала[3]. 2. В позицию рядом с вертикальной осью введите выражение, исходя из которого вы хотите построить график по оси Y. Например, наберите m2 для построения квадратичной функции от m. 3. Щёлкните мышью вне пространства графика. В результате будет получен график с по умолчанию формируемыми интервалами изменения значений аргумента и функции (см. Рис. 2).
На одном пространстве графика можно построить более одного графика.
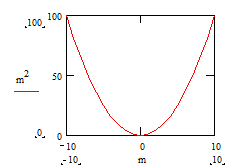
Определение границ интервалов изменения значений аргумента и функции, отображаемых на графике Для определения границ интервалов щелчком мыши выделите пространство графика (диаграммы). Рядом с концами осей графика будут отображены 4 позиции (см. Рис. 3.а) при отсутствии заданной функциональной зависимости или 4 числа при заданной зависимости (см. Рис. 3.б), определяющие границы интервалов изменения аргумента и функции. Щёлкнув мышью на любом из них, вы получите возможность изменения его значения. Для окончания работы с графиком щёлкните вне пространства графика.

Простановка надписей на осях графика Двойным щелчком мыши по графику откройте диалоговое окно. Щёлкните мышью на вкладке Labels. В диалоговом окне Axis Labels введите надписи выбранных вами осей. Для отображения этих надписей на графике (диаграмме) включите соответствующие переключатели: X-Axis – для оси X, Y-Axis – для оси Y. Для подтверждения ввода нажмите “ОК”. Для отмены ввода нажмите “Отмена”. Добавление заголовка в график Щёлкните мышью на графике для открытия диалогового окна. Щёлкните мышью на вкладке Labels. В текстовом окне Title введите заголовок графика. Для вывода заголовка в верхней части графика (диаграммы) включите переключатель "Above", для вывода в нижней части – переключатель "Below". Для отображения заголовка на экране включите переключатель “Show Title”. Для подтверждения ввода нажмите “ОК”. Для отмены ввода нажмите “Отмена”.
Удаление пространства графика Щёлкните мышью на пространстве графика. С помощью этого вы выделите пространство графика квадратом. Нажмите Delete. График будет удалён.
Примеры построения графиков и диаграмм В предыдущих пунктах данного урока было детально объяснено, как построить график (диаграмму) в декартовой системе координат. В данном пункте урока будут приведены примеры построения всех 7 видов графиков и диаграмм. Построение всех графиков (диаграмм) аналогично вышеописанному и подробно повторяться больше не будет.
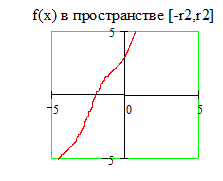
3.2. Построение графиков функций в декартовой системе координат Этот пример показывает, как построить хорошо форматированный график требуемой функции в декартовой системе координат.
Задайте функцию f(x), график которой вы хотите построить:
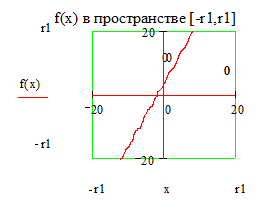
Границы графика: Замечание: В данном примере функция строится в пространстве -r1 x r1, -r1 y r1 и в пространстве -r2 x r2, -r2 y r2. Для создания пространства графика функции f(x) в пространстве с границами по умолчанию установите курсор в пространстве листа и наберите f(x)[Shift]@.
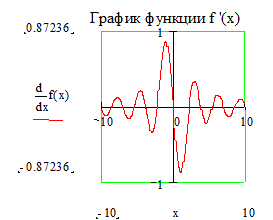
Быстрое построение графика функции и её производной в декартовой системе координат Этот пример показывает, как построить хорошо форматированный график требуемой функции и её производной в декартовой системе координат. Задайте функцию f(x), график которой вы хотите построить:
Для ввода оператора дифференцирования
Быстрое построение дискретно заданной функции в декартовой системе координат
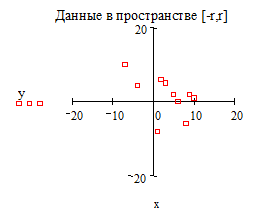
Этот пример показывает, как построить хорошо форматированный график дискретно заданной функции в декартовой системе координат. Задайте матрицу данных (координата X - в первом столбце, координата Y – во втором столбце):
Примечание: Для ввода оператора оператора взятия столбца матрицы Границы графика: Замечание: В данном примере функция строится в пространстве -r x r, -r y r. Для создания графика в пространстве, выбираемом MathCAD по умолчанию перейдите в рабочее пространство всего листа м наберите y@x[Enter].
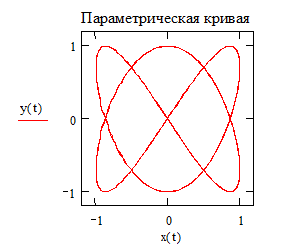
3.3. Построение кривых, заданных параметрически Этот пример показывает, как построить график кривой, координаты точек которой являются функциями одного параметра. Задайте x и y как функции одного параметра t:
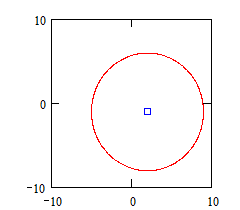
Построение графика окружности Этот пример может быть использован для построения графика окружности заданного радиуса, с заданными координатами центра. Задайте значение координаты x центра: Задайте значение координаты y центра: Задайте значение радиуса окружности: Границы графика:
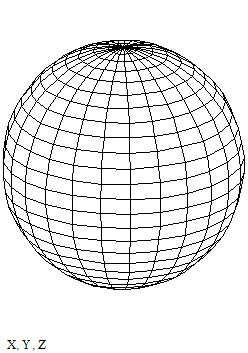
Построение сферы Этот пример может быть использован при построении графика параметрически заданной сферы. Задайте количество параллелей:
3.4. Построение поверхности вращения вокруг оси X
Этот пример может быть использован при построении поверхности вращения функции f(x) вокруг оси X.
Задайте функцию f(x):
Задайте верхнюю и нижнюю границы интервала изменения переменной x:
График функции f(x) на Поверхность вращения: заданном интервале:
3.5. Построение поверхности вращения вокруг оси Y Этот пример может быть использован при построении поверхности вращения функции f(x) вокруг оси X. Задайте функцию f(x): Задайте верхнюю и нижнюю границы интервала изменения переменной x:
График функции f(x) на Поверхность вращения: заданном интервале:
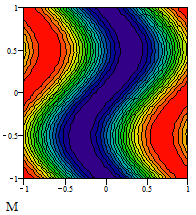
3.6. Построение линий уровня функции двух переменных Этот пример может быть использован при построении линий уровня как функции двух переменных. Задайте функцию двух переменных: Задайте границы интервала изменения переменной х: Задайте количество точек разбиения интервала изменения переменной х:
Задайте границы интервала изменения переменной y: Задайте количество точек разбиения интервала изменения переменной y:
Линии уровня:
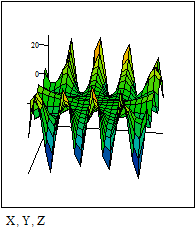
3.7. Быстрое построение трёхмерной интерполированной поверхности Этот пример может быть использован при построении трёхмерной проинтерполированной поверхности, как функции от двух переменных, заданной вами. Задайте функцию f(x,y), график которой вы хотите построить:
Задайте интервалы изменения переменных x и y: Примечание: В этом примере функция отображается в пространстве -xr x xr, -yr y yr. Задайте количество точек дискретизации: Программа нахождения отдельных точек поверхности:
График трёхмерной дискретизированной График проинтерполированной поверхности: поверхности:
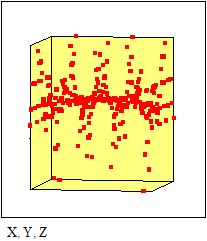
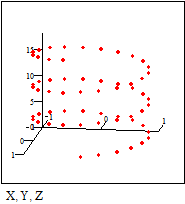
3.8. Быстрое построение кривой в трёхмерной системе координат Этот пример может быть использован при построении графика дискретной функции в системе координат X-Y-Z. Задайте количество точек дискретизации: Определите координаты точек по каждой из осей:
График трёхмерной дискретной функции:
Урок 4. Вектора, матрицы, переменные-диапазоны
4.1. Создание векторов и матриц <small> Для создания матрицы размером до ста элементов требуется выполнить следующие действия: Либо выберите пункт меню Matrix из меню Insert, для появления диалогового окна, с просьбой ввести высоту и ширину матрицы, либо на панели с основными компонентами нажмите кнопку
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.76.111 (0.018 с.) |













 При выполнении вычислений возможны ошибки. Система выводит сообщения об ошибках, закрашивая ошибочные имена идентификаторов в ярко красный цвет. В прежних версиях MathCAD сообщения об ошибках появлялись в красных прямоугольниках с линией, отходящей от места ошибки к прямоугольнику с сообщением о ней. Однако это загромождало документ и от этого способа в новой версии отошли. В новой версии MathCAD подробное сообщение об ошибке тоже можно получить, установив на выражение с ошибкой курсор мыши и нажав ее левую клавишу. Сообщения об ошибках кратки, но их анализ не вызывает особых затруднений.
При выполнении вычислений возможны ошибки. Система выводит сообщения об ошибках, закрашивая ошибочные имена идентификаторов в ярко красный цвет. В прежних версиях MathCAD сообщения об ошибках появлялись в красных прямоугольниках с линией, отходящей от места ошибки к прямоугольнику с сообщением о ней. Однако это загромождало документ и от этого способа в новой версии отошли. В новой версии MathCAD подробное сообщение об ошибке тоже можно получить, установив на выражение с ошибкой курсор мыши и нажав ее левую клавишу. Сообщения об ошибках кратки, но их анализ не вызывает особых затруднений.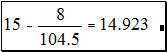
 . Посмотрим, как при этом используется выделяющая рамка:
. Посмотрим, как при этом используется выделяющая рамка: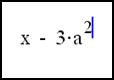
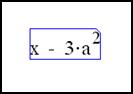
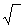 на арифметической палитре. Затем напечатайте под радикалом y+1, чтобы завершить знаменатель.
на арифметической палитре. Затем напечатайте под радикалом y+1, чтобы завершить знаменатель. , производимый [Ctrl]+[Z].
, производимый [Ctrl]+[Z].

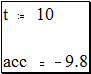
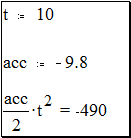
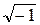 , то MathCAD вернёт i.
, то MathCAD вернёт i.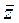
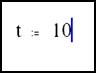
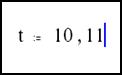
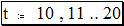


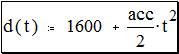
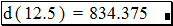
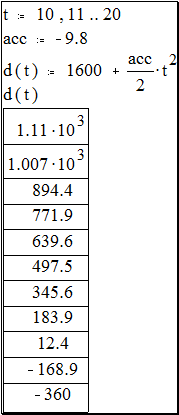


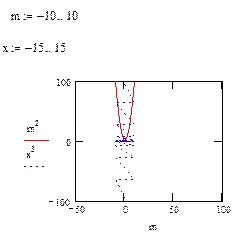
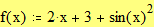
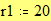
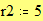
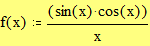
 наберите?.
наберите?.

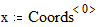
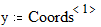
 наберите Ctrl+6.
наберите Ctrl+6.
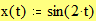
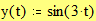
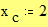

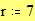

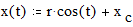

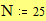
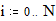
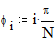
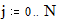
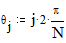
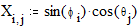
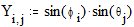

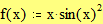
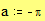

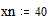
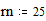
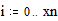
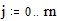
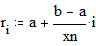
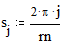
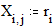
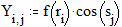


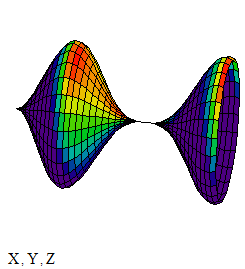


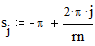
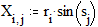
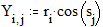
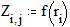



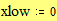


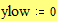
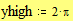
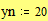
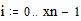
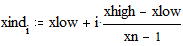
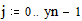
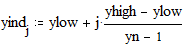
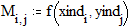
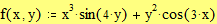
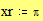

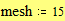
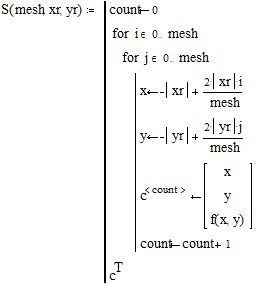
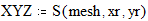






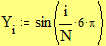
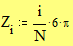
 </small><small>, а на появившейся панели кнопку
</small><small>, а на появившейся панели кнопку  </small><small>, в результате чего на экране появится то же диалогово
</small><small>, в результате чего на экране появится то же диалогово 


