Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение системы нелинейных дифференциальных уравнений.Содержание книги
Поиск на нашем сайте
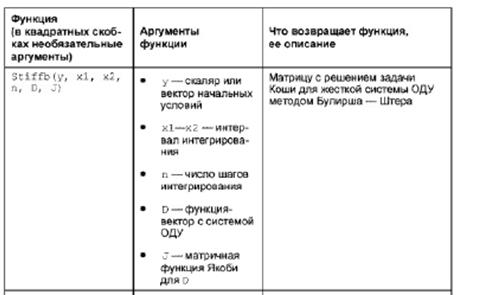
Общим правилом для различных методов численного решения дифференциальных уравнений (ДУ) или системы ДУ является разбиение непрерывной функции y(t) на интервалы (шаги) и определение решения в конце каждого шага, т.е. в дискретные моменты времени, путем некоторой итерационной процедуры. В Mathcad решить задачу Коши для такой системы можно с помощью следующих функций: rkfixed(y, x1, x2, npoints, D) —решение задачи на отрезке методом Рунге—Кутты с постоянным шагом; Rkadapt(y, x1, x2, npoints, D) —решение задачи на отрезке методом Рунге—Кутты с автоматическим выбором шага; rkadapt(y, x1, x2, acc, npoints, D, kmax, save) —решения задачи в заданной точке методом Рунге-Кутты с автоматическим выбором шага; Bulstoer(y, x1, x2, npoints, D) —решение задачи на отрезке методом Булирша-Штера; bulstoer(y, x1, x2, acc, npoints, D, kmax, save) —решение задачи в заданной точке методом Булирша—Штера; Stiffr(y, x1, x2, acc, D, J) — решение задачи для жестких систем на отрезке с использованием алгоритма Розенброка; stiffr(y, x1, x2, acc, D, J, kmax, save) —решения задач для жестких систем на отрезке с использованием алгоритма Розенброка; Stiffb(y, x1, x2, acc, D, J) —решение задачи для жестких систем на отрезке с использованием алгоритма Булирша—Штера; stiffb(y, x1, x2, acc, D, J, kmax, save) —решение задач для жестких систем в заданной точке с использованием алгоритма Булирша—Штера. Смысл параметров для всех функций одинаков и определяется математической постановкой задачи: y — вектор начальных условий
Результат работы функции — матрица, содержащая n+1; ее первый столбец содержит координаты узлов сетки, второй столбец — вычисленные приближенные значения решения y1 (x) в узлах сетки, (k+1) -й — значения решенияyk (x) в узлах сетки. При решении задачи Коши для дифференциального уравнения первого порядка результат вычислений всех приведенных выше функций — матрица, в первом столбце которой содержатся координаты узлов сетки x0, x1,..., xN, а во втором — значения приближенного решения в соответствующих узлах.
Для поиска решения системы ДУ с применением функций rkfixed и Rkadapt, с помощью которых производятся вычисления по методу Рунге-Кутта, необходимо задать: 1) начальные условия; 2) дифференциальное уравнение, представляемое в виде системы ДУ первого порядка; 3) значения коэффициентов, входящих в уравнения; 4) набор точек, в которых следует найти решение. В функцию rkfixed(y,x1,x2,n, F) входят следующие параметры: y – вектор начальных условий с размерностью, соответствующей порядку k ДУ или числу уравнений первого порядка в системе ДУ; x1,x2 – граничные значения интервала, на котором ищется решение; n – число фиксированных шагов или точек, на которых ищется приближенное решение; F – вектор, в котором записаны правые части ДУ В результате решения ДУ с помощью этих функций получается матрица, содержащая (k+1) столбцов и (n+1) точек. В первом столбце содержатся фиксированные значения аргумента t0,t1,t2,…tn; во втором – соответствующие им значения искомой функции y(t0), y(t1), y(t2),… y(tn), в третьем – значения первых производных в тех же узлах и т.д. Функция rkfixed ищет приближенное решение с постоянным шагом, с помощью функции Rkadapt осуществляется адаптивный контроль этого процесса: с более мелким шагом при быстром изменении функции и более крупным – при медленном изменении функции.[1] Жесткие системы. Например, в решении системы ДУ присутствуют слагаемые, одно из которых убывает очень быстро (е-1000х), а другое гораздо медленнее (е-2х). Для получения правдоподобного результата нужно выбирать маленький шаг, причем, на всем интервале интегрирования. Для интегрирования таких систем применяют специальные методы. Эти методы в MathCAD реализуют функции Stiffb, Stiffr. [2]
В таблице приведены некоторые функции для решения систем ДУ.
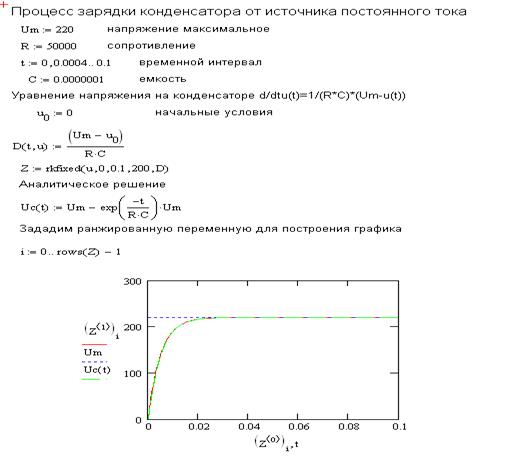
Пример программы решения системы ДУ.
Программирование в MathCAD В MathCAD имеется специальная панель инструментов для ввода программных модулей. Программный модуль выделяется в тексте документа вертикальной жирной чертой.
Построение графиков. График должен располагаться ниже формулы, задающей его. Удаление, копирование и перенос графиков осуществляется по той же методике, что и математических выражений. Изменение размера графика осуществляется путем протаскивания курсора, установленного на обрамляющей его рамке. Создание графика осуществляется командой Insert-Graph или с помощью панели инструментов Graph.
|
||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.205.92 (0.008 с.) |

 ,
, 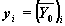 ; x1, x2 — начальная и конечная точки отрезка интегрирования системы; для функций, вычисляющих решение в заданной точке, x1 — начальная точка, x2 — заданная точка; npoints — число узлов на отрезке [x1, x]; при решении задачи на отрезке результат содержит npoints+1 строку; D — имя вектор-функции D(x,y) правых частей
; x1, x2 — начальная и конечная точки отрезка интегрирования системы; для функций, вычисляющих решение в заданной точке, x1 — начальная точка, x2 — заданная точка; npoints — число узлов на отрезке [x1, x]; при решении задачи на отрезке результат содержит npoints+1 строку; D — имя вектор-функции D(x,y) правых частей  ,
,  ; (имя D – от Derivative — производная, имя вектора, содержащего выражения для производных (derivatives) искомого решения); J — имя матрицы-функции J(x,y) размерности n x (n+1), в первом столбце которой хранятся выражения частных производных по x правых частей системы, а в остальных n столбцах содержится матрица Якоби правых частей:
; (имя D – от Derivative — производная, имя вектора, содержащего выражения для производных (derivatives) искомого решения); J — имя матрицы-функции J(x,y) размерности n x (n+1), в первом столбце которой хранятся выражения частных производных по x правых частей системы, а в остальных n столбцах содержится матрица Якоби правых частей: .
.