
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 3. гальванические элементыСодержание книги
Поиск на нашем сайте
Электрический ток можно получать с помощью гальванических элементов или химических источников тока (ХИТ) – замкнутой электрохимической системы, состоящей из двух соединенных между собой электродов, представляющих собой проводник первого рода, погруженный в электропроводящий раствор (проводник второго рода). Электрическая энергия в ХИТ возникает за счет самопроизвольного протекания на электродах окислительно-восстановительных (токообразущих) химических реакций. Для получения во внешней цепи гальванического элемента электрического тока, т.е. направленного движения электронов, необходимо, чтобы процессы окисления и восстановления активных веществ были пространственно отделены друг от друга, а электроды контактировали между собой через электролит. Например, гальванический элемент Якоби-Даниэля (рис. 3.1) состоит из цинкового электрода, погруженного в раствор своей соли, – сульфата цинка ZnS04, и медного электрода, погруженного в раствор СuS04. Растворы разделены пористой перегородкой, которая не дает возможности им смешиваться друг с другом. Схема элемента записывается следующим образом: (-)Zn|ZnSO4||CuS04|Сu(+) (3.1) Вертикальная черта означает границу раздела между твердой и жидкой фазой, две вертикальные черты – границу раздела между растворами электролитов. Пористая перегородка обеспечивает только движение ионов и ее роль сводится к изоляции окисленной и восстановленной форм реагирующих веществ (с тем, чтобы они могли обмениваться электронами только через внешнюю цепь, а не непосредственно). Кроме пористой перегородки существует и другой способ соединения растворов. Это U-образные трубки – электролитические ключи (соляные мостики), содержащие в виде растворов такие вещества, как КС1 или КNO3, подвижность катиона и аниона которых примерно одинакова. Соляные мостики используют для уменьшения диффузионной разности потенциалов, возникающей между растворами за счет различной скорости движения ионов.
Рис. 3.1. Схема элемента Якоби-Даниэля
При разомкнутой внешней цепи на границе раздела цинковой пластины и раствора ZnSO4 устанавливается динамическое равновесие: Zn ↔ Zn2+ + 2 e. (3.2) При этом цинк, как активный металл, заряжается отрицательно, и при соединении с медным электродом будет являться анодом внутренней цепи гальванического элемента. На поверхности раздела медного электрода и раствора CuS04 идет процесс внедрения ионов металла из раствора в кристаллическую решетку пластины, на меди также установится динамическое равновесие: Сu2+ +2е ↔Сu0. (3.3) Медная пластинка при этом заряжается положительно и служит катодом внутренней цепи. При замыкании проводником внешней цепи электроны с цинковой пластины будут переходить на медную. В этом случае цинковый анод будет окисляться и посылать свои ионы в раствор, а на медной пластине – катоде будет идти процесс восстановления. Суммарное уравнение процессов, протекающих в элементе, записывается следующим образом: ● в ионной форме Zno + Cu 2+ →Zn 2+ + Cuo; ● в молекулярной форме Zn + CuS04 → ZnSO4 + Сu. Металлические электроды, погруженные в растворы своих солей, относятся к электродам первого рода. По уравнению Нернста, потенциал такого электрода равен: где Eo – стандартный электродный потенциал металла – электродный потенциал при активности ионов металла в растворе, равной единице; R – универсальная газовая постоянная; F – число Фарадея; n – число электронов, участвующих в окислительно-восстановительной реакции; [aMen+] – активность ионов металла в растворе. Активность ионов в растворе (активная концентрация) связана с аналитической концентрацией «С» уравнением а = γ∙С, где γ – коэффициент активности, учитывающий ионное взаимодействие. В случае разбавленных растворов вместо величины активности можно пользоваться величиной концентрации ионов металла. Тогда уравнение Нернста будет выглядеть следующим образом: где [Ме n+] – концентрация ионов металла в растворе, моль/л. Если подставить значение R = 8,31 Дж/моль и F = 9,65.104 кл/моль, то при Т = 298°К с учетом перевода натурального логарифма в десятичный уравнение (3.5) примет вид
Конкретно для цинкового электрода при Т = 298 К
а для медного электрода
Электродвижущая сила (ЭДС) химического источника тока определяется как разность потенциалов катода и анода. Так как ЭДС – положительная величина, для ее определения следует от потенциала электрода с более положительным значением, которое соответствует катоду, вычесть менее положительное значение потенциала анода: ∆E = Eк - Eа, (3.9) где ∆E − ЭДС; Ек − потенциал катода; Еа − потенциал анода. Измерение электродвижущей силы (ЭДС) проводится на бестоковом режиме, когда внешняя цепь разомкнута и движение ионов под действием поля вообще отсутствует. Для измерения ЭДС обычный вольтметр использовать нельзя, так как в этом случае через цепь потечет ток I и появится падение напряжения I∙R, которое уменьшит величину ЭДС элемента. Поэтому для измерения ЭДС гальванических элементов применяют потенциометры, позволяющие определить разность потенциалов компенсационным методом (измерение при отсутствии тока в цепи), или высокоомные вольтметры. Стандартное значение ЭДС гальванического элемента Якоби-Даниэля
где Величину ЭДС можно также определить, если для химической реакции, протекающей в гальваническом элементе, известны термодинамические функции: изменение энергии Гиббса ∆G, изменение энтальпии ∆H и изменение энтропии ∆S, которые связаны между собой уравнением Гиббса-Гельмгольца: ∆G = ∆H - Т∆S. (3.11) Равновесное значение ЭДС ∆Е (т.е. измеренное в обратимых условиях, при которых ЭДС элемента точно уравновешена внешним напряжением и происходит перенос бесконечно малого количества электричества), связано с изменением энергии Гиббса ∆G следующим образом: ∆G = -n ∙ F ∙ ∆Е, (3.12) где n − число электронов, участвующих в токообразующей реакции при взаимодействии 1 моля вещества; F − число Фарадея. Таким образом, изменение энергии Гиббса равно максимально полезной химической работе, которую совершает гальванический элемент.
|
||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 160; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.38.184 (0.01 с.) |


 , (3.4)
, (3.4) , (3.5)
, (3.5)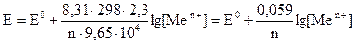 . (3.6)
. (3.6) 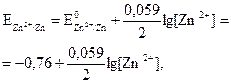 (3.7)
(3.7) 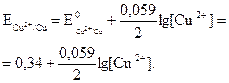 (3.8)
(3.8)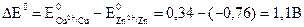 , (3.10)
, (3.10)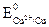 и
и  − стандартные значения электродных потенциалов меди и цинка.
− стандартные значения электродных потенциалов меди и цинка.


