
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Систематические погрешности (СП). М-ды их выявления и исключения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Систематическими наз-ся погрешн-ти не изменяющиеся с течением времени. Основным отличительным признаком явл-ся то, что они могут быть предсказаны и благодаря этому практически устранены введением поправок. Систематич. погрешн-ти могут быть постоянными или изменяющимися во времени функциями. Опасность постоян. Систем-ких погрешностей: их присуствие трудно обнаружить, т.к. они себя никак не проявляют. Их можно обнаружить при проверке прибора, МА и путем сравнения результатов измерений. Прогрессирующие погрешн-ти – погрешн-ти медленно изменяющиеся во времени, кот-е возникают из-за старения деталей. М-д замещения: сравнение осуществл-ся заменой измеряемой величины известной величиной, так, что при этом состоянии и действии всех используемых СИ, не происходит никаких изменений. М-д противопоставления: измерение выполняется дважды и проводится так, чтобы причина постоян. погрешн-ти оказывала разные, но известные по закономерности действия на результат измерения. М-д компенсации погрешн-ти по знаку: сравнение с 2-мя наблюдениями, выполняемыми так, чтобы постоян. систематич. погрешн-ть входила в результат каждого из них с разными знаками. М-д рандолизации: одна и та же величина измеряется разными методами (приборами). Систематич. погрешн-ть для всей совокупности является разными случайными величинами. При увеличении числа м-дов систематич. погрешн-ть взаимно компенсируется. Для устранения переменных и монотонно изменяющихся СП применяются следующ. м-ды: Анализ знаков неисправленных СП: если знаки неисправленных СП чередуются с какой-либо закономерностью, то наблюдается переменная СП. Если последовательность знаков + у СП сменяется последовательностью знаков – или наоборот, то присутствует монотоннноизменяющаяся СП, следовательно присутствует периодическая СП. Графический м-д: построение графика последовательности неисправленных значений результатов наблюдений. Проводят плавную кривую, кот-ая выражает тенденцию результата измерения, если тенденция непрослеживается, Ио переменная СП практически отсутствует. Способ последовательных разностей: для обнаружения изменяющейся во времени СП. Дисперсию результатаов наблюдений можно оценить 2-мя способами: обычным и вычислением суммы квадратов последовательных разностей. Если в процессе измерений происходило смещение в центре группирования результатов наблюдений, тоесть имела место переменная СП, то величина дисперсии дает приувеличенную оценку результатов наблюдений. Это объясняется тем, что на нее влияют вариации среднего значения.
Критическая область для критерия Аббе определяет p(v<vq)=q, q=1-p, где q-уровень значимости, p- доверительная вероятность, vq- в табл. Если v<vq то гипотеза о постоянстве центра группирования результатов наблюдений отвергается, т.е. обнаруживается переменная СП результатов измерений. Дисперсионный анализ: наличие СП результатов наблюдений могут быть обусловлены влиянием постоянно действующего фактора. Для определения этого проводят многократные измерения, из достаточного числа серий, каждая из которых соответствует определен. значениям влияющего фактора. После проведения N измерений их разбивают на S серий по n результатов в каждой (N=S*n), и устанавливают имеется ли систематич-ое расхождение между результатами наблюдений в различных сериях. Результаты в сериях должны быть распределены нормально. Характеристикой совокупности случайных внутрисерийных погрешн-тей будет средн. сумма дисперсии результатов наблюдений, вычисленных раздельно для каждой серии: σ²вс= (1/N-S)∑∑(хij-xjсреднее)², где хij-текущий результата в серии i; xjсреднее- ср. результат j-той серии; n – кол-во рез-в в серии; S- кол-во серий; N-общее кол-во рез-в наблюд-й. Внутрисерийная дисперсия σ²вс характеризует случайные погрешн-ти измерений, т.к. только случайные влияния обуславливают те различия, на которых она основана. Рассеение хij различных серий обуславливается также систематич-ми различиями. Усредлненная межсирийная дисперсия: σ²мс=(1/S-1) ∑(хсреднее – хj среднее) ², где х=(1/N) ∑ nj*xj – выражает сумму действий фактора, вызывающего систематич-кие различия между сериями. Величина σ²вс/ + σ²мс – характеризует долю дисперсии всех результатов наблюдений, обусловленную наличием случайн. погрешностей, а величина σ²мс/ σ²мс+ σ²вс – долю дисперсии, обусловленную межсерийными различиями результатов наблюдений. Чем больше отношение показателя дифференц-х коэф. Ошибки, тем сильнее действие фактора, и тем больше систематическое различие между ними. Критерий оценки наличия СП является дисперсионный критерий Фисшера F= σ²мс/ σ²вс. Критическая обл-ть соответств-т Р(F>Fq)=q.
Значение Fq для различных уролвней значимости q, числа наблюдений N, числа серий приведены в стат-ких табл. Если F>Fq, то гипотеза об отсуствии систематич-х смещений результатов наблюдений по сериям отвергается, то есть обнаруживаются СП, вызываемая тем фактором, по кот-му группировались результаты наблюдений. Критерий Вилкоксона: применяют если з-н распределения результатов неизвестен. Используется для проверки различий между двумя выборками парных измерений. Критерий предназначен для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить не только направленность изменений, но и их выраженность, то есть, способен определить, является ли сдвиг показателей в одном направлении более интенсивным, чем в другом. Суть метода состоит в том, что мы сопоставляем абсолютные величины выраженности сдвигов в том или ином направлении. Для этого сначала все абсолютные величины сдвигов ранжируются, а потом суммируются ранги. Если сдвиги в ту или иную сторону происходят случайно, то и суммы их рангов окажутся примерно равны. Если же интенсивность сдвигов в одну сторону больше, то сумма рангов абсолютных значений сдвигов в противоположную сторону будет значительно ниже, чем это могло бы быть при случайных изменениях. 6. Случайные погрешности (СП) Методы их оценивания на основе теории вероятностей. Случайной погрешностью (СП) наз-ют непредсказуемые ни по знаку, ни по размеру погрешности. Они опр-ся совокуп-ю причин, неподдающихся анализу. СП легко обнаружить при проведении повт. измер-ий. Гл. особенность СП – непредсказуемость от одного отсчёта к другому. СП описыв-ся только на основ-ии теории вероятности и матем. статистики. Присутствие случ. погрешностей (СП) в рез-тах измер-ий легко обнаружив-ся из-за их разброса отн. некот. знач-я – истинного. Из теории вероятн. изв-но, что наиб. универс. сп-бом описания случ. величин (с.в.) явл. отыскание их интегральных и дифференц-ных ф-ций распредел-я. Под интегр. ф-цией распредел-я F(x) поним. ф-цию, каждое знач. кот-й для кажд. х явл. вероятн-тью события, заключ-гося в том что с.в. хi в i-ом опыте измер-я приним. знач. меньше х, т.е. F(x)=Р(х< хi). Св-ва интегр. ф-ции распр-я: 1)она неотрицат-ная; 2) она неубывающая; 3)диапазон её измен-я [0;1]; 4) вероятность нахожд-я с.в. х в диапазоне от х1 до х2: Р(х1<x<x2)=F(x2)-F(x1). Описание распред-я рез-тов измер-я и СП в том числе будет более наглядным с использ-ем дифференц-ной ф-ции распредел-я, наз-емой плотностью распредел-я: р(х) =dF(x)/dx. Учитывая взаимосвязь между интегр. и дифференц. ф-циями очевидно, что вероятность попадания с.в. в интервал от х1до х2: Р(х1<x<x2)= На графике вероятность попадания с.в х в задан. интервал от х1 до х2 равна площади, заключённой под кривой р(х) между абсциссами х1 и х2. В большинстве случаев достаточно охар-зовать с.в. с пом. спец. параметров, осн-ми из кот явл-ся: -центр распределения - нач. и центр. моменты и производные от них коэффиц-ты (мат. ожидание, дисперсия, ассиметрия, эксцесс)
-энтропийный коээфиц-нт. Координата центра распред-я показ. полож-е с.в. на числ. оси. наиб фундамент. явл. центра симметрии, т.е. нахожд-е такой точки на оси х, справа и слева от кот. вероятн-ти появл-я разл. знач. с.в. одинак. и равны 0,5. Данную точку назыв. медианой. Можно опред-ть центр распред-я и как центр тяжести распред-я, т.е такой точки Х, отн-но кот. опрокидывающий момент геометрич. фигуры, огибающей кот. явл. кривая р(х), равен 0. Данную точку назыв. мат. ожиданием. Для симметрич. распред-ий в качестве центра мож исп-ся абсцисса моды, т.е. максимума распред-я. Для огранич. распред. (равном., трапециидального, арксинусоид.) примен-ся оценка в виде центра размаха. При выборе оценки центра распред-я помимо эффект-сти необх-мо учитывать её чувствит-сть к наличию промахов. Оценка в виде центра размаха чувствит-на к наличию промахов, т.к. опред-ся по наиб. удалённым от центра наблюд-ям. Все моменты распред. предст. собой некот. ср.знач-я. Нач. моментом n-го порядка рез-та наблюд. измер-ий явл. интеграл, представляющий собой мат. ожидание вел. х в степ. n: αn=M(x^n). Центр. моментом n-го порядка рез-тов наблюд. наз. интеграл, предст-щий собой мат.ожидание n-ой степ. случ. абс. погрешности: µ=М(х-М(х))^n. Для хар-ки рез-ов наблюд. исп-ся 2-ой центр. момент, кот. наз-ся дисперсией(D). D явл. хар-кой рассеивания с.в. отн. мат. ожидания. Станд. отклон-е СКО= Для того чтобы оценить ассиметрию опр-ся 3-ий центр. момент µ3, хар-ющий несимметричность распред-я. 4ый центр. момент служит для хар-ки плоско или островершинности распред-я. Эти св-ва хар-ся с пом. эксцесса. Чтобы оценить интервал неопрд-сти, в кот. нах. рез-тат многократ. измер-я без каких-либо предполож-ий об ур-не довер-ной вероятн-ти опр-ся энтропийный коээфиц-нт. Всё множ-во з-нов распред-я с.в. классифицир-ся: - трапицеидальные(плосковершинные).к ним отн. равном.,трапециидальное, треуг-ное. - уплащенные(с выраж. коэффиц. эксцесса) предст. сочетание равном. и экспоненц. распред. - экспоненциальные - семейство распред-ий Стьюдента (само распр. Стьюдента, распред. Коши, норм. распред.) - двухмодальное распред-е. Рассм. гр. трапецеидальных распред. на примере равном-го. Если заранее бывает известно, все возм. знач-я СП СИ равновероятны и лежат в пределах некот. интервала, то распред-е таких СП наз-ся равномерным. Знач. дифференц. ф-ции равномернораспред-нной с.в. на интервале от –α до +α пост-нно, а вне этого интервала =0, поэтому выраж-е для дифференц. ф-ции можно записать:
Из графика (парабола) норм. распред-я видно что по мере увелич-я СКО распред-е всё более расплыв-ся, вероятн. появл-я больших знач-ий погрешн-тей возрастает, а вероятность меньших погрешностей сокращ-ся, т.е увелич-ся рассеивание рез-тов наблюд-ий. Шир. распр-ние норм. распред-я хар-ся тем, что распред-е СП будет близко к норм-му всякий раз, когда ре-ты наблюд-я формир-ся под влиянием больш. числа независимо д-ющих факторов, каждый из кот. оказыв. незначит. д-ие по сравн. с сумм. д-ем всех ост-х. ассиметрия норм. распред-я =0, т.к распр-е симетр. отн.0, эксцесс =3. так. обр. равном распред-е –плосковершинное, а норм. – островершинное. Точечные оценки з-нов распред-я можно оценить путём выч-я ср. знач. массива эксперимент. данных (ср. арифметич.), оценить рассеяние массива отн. ср. арифметич. можно с пом. несмещённой оц-ки дисперсии и станд. откл-ния(ско). Причём дисперсия выраж. мощность рассеивания, а станд. откл.явл. д-ющим знач-ем с.в. Оценить ассиметрию, хар-ющую несимметриность распред-я можно с пом. 3-го центр. момента. Степень заострённости з-на распред-я хар-ся эксцессом и опр-ся оценкой 4-го центр. момента. Оценить интервал неопр-сти, в кот. нах-ся рез-т многокр. измер-я можно с пом. энтропийного коэффиц. Аналитич. м-ды опред-я формы з-на распред-я веротян. (ЗРВ) основаны на выч-нии оценок показ-лей формы распр-я: асимметрии, эксцесса, коэффиц. формы кривой распред-я, контрэксцесса, энтропийного коэффициента. При этом найденные оценки сравнив-ся с известн. табличн. знач-ми показ-лей, рассчитанными для разл. теоретич. ф-ций распр-я. Гипотезу о форме ЗРВ, можно выдвинуть после постр-я гистограммы и кумулятивной кривой. Форма гистограммы очень часто зависит от кол-ва интервалов, на кот. разбив-ся весь массив выборки, от располож-я интерв. отн-но хар-ки полож-я (ср. арифм., медианы и т.д.). Поэтому целесообразно строить неск. (не менее 2) гистограмм, кот. мог. отлич-ся друг от друга кол-вом интервалов или (и) др. парам. Окончат. вывод о том, какая гипотеза о форме ЗРВ д. б. подвергнута дальнейш. ан-зу, м. б. сделан после сравн-я формы ЗРВ, получ. по гистограмме, с возм. формами, опр-ми по оценкам показ-лей формы распр-я. Если предварит. вывод о возм. формах ЗРВ, получ. по оценкам показ-лей формы, соотв-ет выводу о форме ЗРВ, получ. на основ-ии постр.-ой гистограммы, то можно гипотезу о форме ЗРВ принять. Если же этого соотв-я не получ-ся, то необх-мо постр. новую гистограмму и выдвинуть по ней другую гипотезу о форме ЗРВ. После опр-я ЗРВ необх. опр-ть рез-т многокр. измер-я ф. в., представив его в виде хар-ки полож-я, доверит. интервалы знач-ий кот-й определены с заданной вероятностью. При этом завис-сть параметра t, с пом. кот. опр-ся доверит. границы, от доверит. вероятн. для кажд. ЗРВ будет разная и располаг-ся м-ду завис-стью, опред-ой для норм. ЗРВ, и опред-ной по нерав-ствву Чебышева. Для получ. ЗРВ необх. построить завис-ть параметра t от доверит. вероятн. и опр-ть по этой завис-сти пределы, в кот. мож. нах-ся хар-ка полож-я для 2-х знач. доверит. вероятности: Р = 0,9 и Р = 0,95.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 578; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.142.235 (0.008 с.) |

 , следв-но вероятн. попадания велич. х в интервал (-∞;+∞)=1.
, следв-но вероятн. попадания велич. х в интервал (-∞;+∞)=1. D.
D.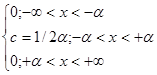 ;
;  . Велич. с=1/2α нах. из усл. что площадьзаключ-я м-ду кривой распред-я и осью абсцисс =1. Для дан. вида ф-ции мат. ожид-е =0. Дисперсия равномерно распред-ной с.в. D(x) = (α^2)/3. В силу симметрии распред-я отн. мат. ожид-я коэффиц. ассим-рии =0. Равном. распред-е симметричное, при увелич-ии СП свыше +α, площадь под кривой распред-я не меняется и интгр. ф-ция распред-я сохр. пост. знач-е, равное 1.
. Велич. с=1/2α нах. из усл. что площадьзаключ-я м-ду кривой распред-я и осью абсцисс =1. Для дан. вида ф-ции мат. ожид-е =0. Дисперсия равномерно распред-ной с.в. D(x) = (α^2)/3. В силу симметрии распред-я отн. мат. ожид-я коэффиц. ассим-рии =0. Равном. распред-е симметричное, при увелич-ии СП свыше +α, площадь под кривой распред-я не меняется и интгр. ф-ция распред-я сохр. пост. знач-е, равное 1.


