
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логические и фактические объемы и содержания понятийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
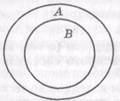
Мы видели, что наряду с определением содержания понятия как совокупности признаков, возможна характеристика его как некоторого предиката. Поскольку предикат представляет собой высказывательную форму, он выражает некоторую информацию о предметах, мыслимых в понятии. В силу этого представление содержания как предиката позволяет истолковать его как характеристику информативности понятия. Различение понятий по информативности существенно для выяснения многих аспектов при анализе этой формы мышления. Оно приводит, в частности, к устранению многих недоразумений, которые возникали в прошлом, в частности, в связи с известным в логике законом обратного отношения между объемами и содержаниями понятий. В распространенной формулировке он гласит: объем и содержание понятия находятся в обратном отношении: чем шире объем, тем уже содержание понятия, и наоборот. Более точно, имеется в виду отношение между объемами и содержаниями двух понятий хА(х) и хВ(х) с одним и тем же родом (область значений χ — D). Согласно закону, если объем одного из этих понятий шире объема другого, то содержания их находятся в обратном отношении. Может быть принята и более общая формулировка: Если объем одного понятия составляет часть объема другого (с тем же родом), то содержание второго составляет часть содержания первого. Кроме того, поскольку понятия имеют один и тот же род, отношение «часть — целое» между содержаниями понятий сводится к отношению между видовыми отличиями этих понятий, т.е. между предикатами А(х) и В(х). Таким образом приходим к формулировке: Объем одного понятия составляет часть другого (с тем же родом), если и только если содержание второго составляет часть содержания первого. Однако, если для объемов понятий мы уже имеем определение отношения «объем одного понятия составляет часть объема другого» (см. §15), то аналогичное отношение для содержаний понятий определить не так просто. Первое, что напрашивается, это — сравнение содержаний понятий по количеству признаков. В таком случае для понятий «число, которое делится на 2 и на 3» и «число, которое делится на 3» вопрос решается просто: содержание первого шире, поскольку больше количество составляющих его признаков. Однако сразу возникает неясность, когда мы рассматриваем понятия «число, которое делится на 2 или на 3» и «число, которое делится на 3». Кажется, что количество признаков в первом также больше, чем во втором, но объем первого также шире, чем объем второго. В таких понятиях как «студент, сдавший все экзамены сессии на отлично» и «студент, сдавший какие-нибудь экзамены сессии на отлично» количество признаков представляется даже одинаковым. Однако они явно различаются по своей информативности. «Сдал все экзамены» безусловно более информативно, чем «сдал некоторые экзамены», и ясно, что объем первого понятия уже, чем объем второго. Ясно также, что «делится на 3» содержит больше информации, чем «делится на 2 или на 3». Кстати, «делится на 2 или на3» — это один признак, он является общим для чисел, обобщаемых в приведенном выше понятии (сравни «слово, обозначающее действие или состояние» среди приведенных выше упражнений). В истории логики известен так называемый парадокс Боль-цано, по видимости, опровергающий закон обратного отношения. Формулируются два понятия: «Человек, знающий европейские языки» (имеются в виду, конечно, все европейские языки) и «Человек, знающий живые европейские языки». Видимость такова, что содержание второго понятия шире, поскольку к характеристике языков добавляется признак «живые», т.е. действующие в настоящее время. Но и объем этого понятия также шире, чем объем первого. Ясно, что всякий, знающий все европейские языки, знает, конечно, и все живые европейские языки, но не наоборот. Отношения между объемами этих понятий может быть представлено схемой: А — человек, знающий все живые европейские языки. В — человек, знающий все европейские языки
Из этой схемы очевидно, что людей, знающих все живые европейские языки, больше, чем людей, знающих все эти языки. Для сравнения признаков по информативности может быть использовано понятие «логическое следование». Если из высказывания или высказывательной формы А логически следует В, т.е. А Ясно, что приведенные выше «парадоксальные случаи» легко разрешаются. Содержание (информация предиката) "х делится на 2 или на 3» составляет часть информации предиката «х делится на 2», поскольку имеет место следование. А следует А следствие первого (вообще Видовое отличие второго понятия выражает предикат «Для всякого европейского языка, если он является живым, то χ знает его» — Однако приведенных уточнений все-таки оказывается недостаточно. Возьмем, например, пары понятий «квадрат» и «квадрат с взаимно перпендикулярными диагоналями», или «число, делящееся на 2 и на 3» и «число, делящееся на 2, на 3 и на 6». Согласно понятию логического следования и введенному определению отношения «часть» для содержаний между понятиями, содержание второго понятия в каждой из этих пар шире, чем содержание первого, однако объемы первого и второго в каждой паре совпадают. Для разрешения трудностей этого рода необходимы определенные уточнения понятий «содержание понятия», «объем понятия», а вместе с тем и формулировки самого закона. Необходимо различать логическое и фактическое содержание понятия и аналогично логический и фактический объемы понятий. Логическое содержание, которое до сих пор, по существу, имелось в виду, — это имеющаяся в понятии информация относительно обобщаемых в нем предметов, зависящая лишь от логической формы понятия. Фактическое содержание — это информация, которую мы имеем в понятии с учетом знаний, имеющихся в его формулировке дескриптивных терминов (знаков предметов, свойств, отношений). «С учетом знаний... дескриптивных терминов» означает «с учетом некоторой совокупности знаний относительно предметов, свойств, отношений — значений этих терминов» в составе некоторой теории, в которой используется данное понятие. Утверждение «фактическое содержание понятия хВ(х)" совокупности знаний Г составляет часть фактического содержания понятия хА(х) и относительно той же совокупности знаний определяется как Ясно, что если логическое содержание В — одного понятия, составляет часть логического содержания А — другого понятия, то это же отношение существует и между их фактическими содержаниями, ибо если Λ Логический объем понятия хА(х) составляет множество возможных предметов х, выполняющих предикат А без учета значений имеющихся в нем дескриптивных терминов, т.е. рассматриваемый лишь со стороны его логической формы. Фактический объем того же понятия — это множество фактически существующих предметов, удовлетворяющих условию А с учетом значений его дескриптивных терминов. Как уже упоминалось, объемы рассмотренных пар понятий, а также следующих — «квадрат» и «квадрат с взаимно перпендикулярными диагоналями», «число, делящееся на 2 и на 3» и «число, делящееся на 2, на 3 и на 6» равны. Теперь уточним: равны именно фактические их объемы. Что касается логических объемов, то для понятий каждой пары они различны. Именно: объем второго понятия в каждой паре уже, чем объем первого. Действительно, если логическую форму первого понятия в первой паре, например, представить как хР(х), а второго — х(Р(х) & Q(x)), то логические объемы их соответственно представляют множество WxP(x) и Wx(P(x) & Q (x)), второе множество уже, поскольку оно равно WxP(x) Как видим из анализа последнего примера, сравнение логических объемов, как, впрочем, и фактических, можно осуществлять, подвергнув их предварительно разложению на некоторые составляющие. Формулировка закона обратного отношения должна быть уточнена теперь с учетом проведенных различений фактических и логических содержаний и объемов понятий. Ясно, что если мы сравниваем фактические объемы (или содержания) двух понятий, то соответственно должны рассматриваться отношения между фактическими содержаниями (или объемами). Отношению между логическими объемами (или содержаниями) соответствует отношение между логическими же содержаниями (объемами). Приведенные выше примеры казались опровергающими закон обратного отношения потому, что рассматривая отношения между объемами, мы брали фактические объемы, а содержания при этом имели в виду логические!По существу, мы имеем теперь два закона обратного отношения: с одной стороны, для фактических содержаний и объемов, с другой — для логических. Приведенная выше формулировка относится именно к этому последнему закону. В качестве обобщающей их формулировки может быть принята следующая (закон обратного где Г указывает на то, что сравнение объемов и содержаний осуществляется с учетом совокупности знаний Г. есть то же, что и Этот закон играет важную роль во многих процессах познания. По существу, он является основой в семантической теории информации. Само понятие семантической информации, например, информации того или иного высказывания А, определяют обычно как меру или показатель того, насколько принятие этого высказывания за истину ограничивает некоторое множество исходных возможностей М. Информативность А тем больше, чем сильнее это ограничение. Если мы, например, говорим, что данное вещество химически сложно, то ограничиваем множество химических веществ до химически сложных; утверждение же о том, что это вещество является химически сложным и состоит из кислорода и водорода, делает круг возможностей, к которому относится рассматриваемое вещество, еще более узким и, значит, является более информативным. Наше утверждение относится, вообще говоря, не к действительности в целом, например, не к миру вообще, а к некоторым его состояниям в те или иные моменты или промежутки времени, или, как говорят в логике, к возможным мирам, которые представляют так называемые «описания состояний». На этом основан широко применяемый в логике и теории информации способ оценки информативности логических форм высказываний. Информация при этом определяется относительно множества «возможных миров М". Логическая форма А некоторого высказывания Упражнения 1. В каком отношении находятся содержания (фактические и логические) следующих пар понятий и каково отношение между их объемами: а) плоский замкнутый четырехугольник с равными противоположными сторонами (параллелограмм) и плоский замкнутый четырехугольник с равными сторонами (ромб)? б) число, делящееся на 6, и число, делящееся на 6 и на 3? 2. Известно, что всякая фигура, у которой противоположные стороны параллельны, есть фигура, у которой противоположные стороны равны. Что можно заключить из данной характеристики отношений между фактическими объемами понятий об отношении их содержаний? Виды понятий Вопрос о видах понятий — это прежде всего вопрос о различных способах мысленного выделения и обобщения предметов в процессе познания. Знание видов понятий важно прежде всего с гносеологической точки зрения, для понимания процесса познания. Но оно имеет и немалую практическую значимость. А именно, оно важно для понимания смыслов тех или иных утверждений, а также для обеспечения точности выражения мыслей. Таким образом, это знание является существенным моментом логической культуры мышления. Различение видов понятий осуществляется с разных точек зрения главным образом по трем основаниям: I) по некоторым характеристикам объемов понятий; II) по характеру признаков, составляющих видовое отличие мыслимых предметов в понятии, точнее говоря, по характеру предиката, выражающего это видовое отличие, т.е. предиката А(х) в понятии хА(х); III) по характеру предметов, обобщаемых в понятии. I. Среди всех возможных понятий обычно особо выделяют пустые и непустые, а среди непустых — единичные и общие. Пустые понятия имеют в качестве объема пустой класс. Полезно различать понятия логически и фактически пустые. Понятие хА(х) является логически пустым, если А(х) есть логически противоречивая характеристика предметов х. Ясно, что в силу законов логики пустым является любое понятие вида х(Р(х) & & Возможность появления пустых понятий объясняется тем, что в научном мышлении понятия возникают не только о тех предметах, которые имеются налицо. На основе познанных процессов, законов часто возникают предположения о существовании или возможности появления тех или иных явлений с заранее определенными признаками («антиатомы», «растительность на Марсе» и т.п.). Здесь новые понятия возникают на основе других понятий и знаний как проявления активного и творческого характера мышления. Естественно, что в таких случаях могут возникать понятия, которым, как оказывается затем, ничего не соответствует в действительности. Но в некоторых случаях наука сознательно использует пустые понятия даже для формулировки некоторых законов. Читателю известны два закона термодинамики: один из них гласит, что невозможны «вечные двигатели» 1-го рода, второй гласит то же самое о «вечных двигателях» 2-го рода. Единичным является понятие, объем которого есть единичный класс, а общие понятия имеют в качестве объема класс, состоящий более чем из одного предмета. Единичное понятие по сути своей представляет собой, как и всякое другое, некое обобщение и этим отличается от имени отдельного предмета. Мы не всегда при этом можем даже знать, что класс обобщаемых предметов является именно единичным. Без дополнительных знаний не ясно, например, является ли общим или единичным понятие «город, породненный с Волгоградом». Возможно, не каждому известно, что в объем этого понятия входят 9 городов в разных странах мира.В некоторых случаях возникают трудности при попытке решить вопрос, является ли некоторое понятие общим или единичным в силу характера мыслимых в понятии предметов. Едва ли могут возникнуть сомнения насчет того, являются ли общими такие, например, понятия, как «человек», «растение», «город», «страна». Но уже не так легко определить, к какому классу относятся понятия «вода», «водород» и т.п., вообще понятия, в которых обобщаются газообразные, жидкие или сыпучие вещества, т.е. объекты, трудно поддающиеся индивидуализации. Аналогичные трудности возникают с понятиями «любовь», «бытие» и т.п. (так называемые абстрактные понятия). Полезно использовать в таких случаях следующий критерий: понятие является общим, если в пределах его объема могут быть выделены некоторые виды предметов. Так, в объеме понятия «вода» мы можем выделить: «морская вода», «речная вода», «дистиллированная» и «недистиллированная вода». В объеме понятия «бытие» (имея в виду способ существования чего-либо), выделяют «бытие отдельного человека», «общественное бытие». (Сравним утверждения диалектического материализма «бытие определяет сознание» и «общественное бытие» определяет «общественное сознание».) «Любовь», как известно, также различают — «страстная» и «спокойная», «вечная» и «непостоянная», «бескорыстная» и по «по расчету». Еще более просто решить указанный вопрос, когда возможна индивидуализация мыслимых в понятии объектов. Так, пользуясь понятиями «талант» или «белизна», мы выделяем индивидуальные случаи: «талант Пушкина», «талант Толстого», «белизна снега», «белизна мела». Что касается понятий «вода», «водород», то элементами объема здесь являются отдельные случаи, когда мы встречаем эти вещества в природе (отдельные порции или отдельные скопления их). Однако в данном случае речь идет о повседневном употреблении соответствующих терминов. Иное дело, когда эти термины употребляются специальным образом, например, в химии. Термин «вода» в этом случае выражает единичное понятие «химически сложное вещество, молекулы которого состоят из двух атомов водорода и одного атома кислорода». Аналогично этому «водород» есть определенное химически простое вещество или химический элемент (в связи с тем, что эти понятия являются единичными, выражающие их термины могут употребляться и как имена соответствующих веществ или элементов). Среди общих понятий особое место занимают так называемые универсальные понятия. Универсальными являются понятия вида хА(х), объем которых совпадает с областью значений х, т.е. с родом этого понятия. Это совпадение обусловлено тем, что предикат А(х) не содержит никакой информации относительно предметов рода и, значит, ничего не выделяет в этом роде. Аналогично тому, как мы среди пустых понятий различаем логически и фактически пустые понятия, мы различаем логически и фактически универсальные понятия. Например, логически универсальным является Указанное различие внутри универсальных и пустых понятий связано с приведенным выше различением логических и фактических содержаний и соответственно объемов понятий. Нетрудно усмотреть следующую связь между пустыми и универсальными понятиями: если хА(х) пусто, то II. По характеру признаков выделяют обычно положительные и отрицательные, относительные и безотносительные понятия. Понятие хА(х) положительно, если А(х) выражает наличие у предметов χ какого-либо свойства или отношения и отрицательно, если признак А(х) указывает на отсутствие какого-либо свойства или отношения. Пользуясь данными выше определениями положительного и отрицательного признаков, можно сказать, что понятие является положительным или отрицательным в зависимости от того, положительным или отрицательным является признак А(х). Понятие хА(х) положительно, если А(х) выражает наличие у предметов χ каких-то свойств или отношений. Положительными являются, например, понятия «европейское государство»,«столичный город», «родственники». Примеры отрицательных понятий — «человек, не знающий логики», «непересекающиеся прямые», «нечестный и безнравственный человек». Безотносительным или относительным понятие является в зависимости от того, представляет ли его видовое отличие атрибутивное или реляционное свойство (см. §12). Безотносительными являются, например, понятия: «кристаллическое вещество», «преступное действие», «рентабельное предприятие». Относительными будут: «отец А.Македонского», «столица Франции», «столица какого-нибудь государства». Можно выделить три основных вида относительных понятий по их знаковым формам:
Первые два из приведенных примеров относятся к виду 1. Третий — к виду 2. Понятиями, относящимися к виду 3, будут «студент, сдавший все экзамены сессии», «человек, не знающий ни одного иностранного языка». III. По характеру обобщаемых в понятии объектов следует различать прежде всего понятия, в которых обобщаются отдельные предметы того или иного типа Дальнейшее подразделение относится к понятиям вида Абстрактные объекты — суть создания мысли, идеальные предметы. Таковы те или иные характеристики конкретных предметов (свойства их, предметно-функциональные характеристики или отношения между ними), отвлеченные от соответствующих предметов и ставшие самостоятельными объектами мысли. Так возникают «числа, фигуры, движение». К множеству объектов этого типа можно, очевидно, также отнести параллели, меридианы, векторы и т.п. Конкретным является понятие, элементы объема которого — конкретные объекты. Таковы понятия, составляющие смысл выражений «человек», "социалистическая революция», «растение», «государственная собственность некоторой страны» и т.п. Абстрактные понятия в качестве элементов объема имеют абстрактные объекты. Таковы понятия: «число», «геометрическая фигура», «арифметическая функция», «рефлексивное и симметричное (двухместное) отношение», а также «хозрасчет», «метод бригадного подряда» и т.п. Заметим, что в логической литературе определения конкретных и абстрактных понятий не вполне совпадают с данными здесь их характеристиками. Обычно говорят, что элементами конкретных понятий являются предметы, представляющие собой — с логической точки зрения — некоторые системы признаков, т.е. некоторые конкретные предметы, а элементами объема абстрактных понятий являются отдельные характеристики (стороны, свойства) конкретных предметов. Понятие «геометрическая фигура» относится в таком случае к числу конкретных понятий, а абстрактными будут: «площадь геометрической фигуры», «замкнутость геометрической фигуры» и т.п. Однако это различение весьма неопределенно, поскольку и отдельные свойства, и отношения предметов в свою очередь представляют собой какую-то систему свойств (более высокого порядка) и поэтому подходят под определение конкретных объектов. Впрочем, и та граница, которая подразумевается в различении, проведенном нами первоначально, тоже не является вполне четкой. Как известно, нет строгих граней даже между более простыми предметами и явлениями действительности, и почти любое различение видов тех или иных предметов в той или ной степени условно и неопределенно. Понятие свойства (как и отношения) возникает в результате двойного абстрагирования. С одной стороны, происходит отвлечение некоторого свойства от предметов — изоляция его от предметов и превращение в самостоятельный предмет (изолирующее абстрагирование); с другой стороны, осуществляется обобщение этого свойства путем выделения общих основных свойств этих свойств и отвлечения от остальных (обобщающе - различающее абстрагирование). Существуют неясности, связанные с абстрактными понятия-Ми. Например, бывают они общими или только единичными, Как считают многие авторы учебников по логике? Имеет ли смысл их деление на относительные и безотносительные? Ясно, что среди абстрактных понятий имеются как общие, так и единичные. Независимость государства имеет виды: политическая независимость, экономическая независимость и т.д. Это означает, что понятие является общим. Далее, если иметь в виду абстрактные понятия, в которых мыслятся свойства, отношения и тому подобные характеристики конкретных предметов, то все они, очевидно, являются относительными, поскольку для содержания каждого такого понятия обязательными являются указания на принадлежность мыслимой характеристики тому или иному отдельному предмету или каким-то из предметов некоторого класса. Например, «независимость Кампучии», «независимость (некоторого, какого-либо) государства». Значительная доля условности имеется и в делении понятий на собирательные и несобирательные. Несобирательными называются понятия, предметы которых представляют собой нечто целое, хотя и состоящее возможно из каких-то различных частей, но мыслимое как нерасчлененное целое. Например, физическое тело», «человек», «растение». Конечно, каждое тело является, как мы знаем, совокупностью молекул и других частиц, но в несобирательном понятии мы отвлекаемся от его структуры и вообще от того, что оно представляет собой какую-то структуру. Предметы, обобщаемые в собирательных понятиях, т.е. элементы объема такого понятия, это некоторая совокупность (возможно, даже отдельно существующих предметов) или система предметов, мыслимая как целое. Например, «производственная бригада», «народ», «флот», «лес» и т.п. Объем понятия «производственная бригада» есть совокупность всех возможных производственных бригад (таким образом, понятие является общим), и содержание понятия «совокупность людей, соответствующим образом организованных для выполнения определенных производственных задач» относится к каждой из них, но, конечно, не к отдельным членам бригады. Очевидно, что собирательное понятие может быть и единичным, например, «студенческий коллектив МГУ», «созвездие Большой Медведицы» и др. Отдельные предметы, составляющие совокупности, мыслимые в собирательном понятии, вообще говоря, существуют или могут существовать отдельно или самостоятельно. Но в некоторых отношениях их совокупность выступает как одно целое (например, перед всеми людьми, составляющими производственный коллектив, стоят некоторые общие задачи, и все они в совокупности несут ответственность за их выполнение и т.д.). Это обусловливает возможность и необходимость в некоторых случаях мыслить совокупность как один предмет. Иногда говорят, что собирательные понятия могут употребляться в разделительном смысле. Так, как будто, употребляется собирательное понятие «данный коллектив» в суждении: «Все члены данного коллектива справились со своим заданием». Однако точнее сказать, что в данном суждении сам предмет (данный коллектив), а не понятие, берется разделительно, хотя бы потому, что члены коллектива являются частями коллектива, но не являются ни частями, ни элементами объема понятия «данный коллектив». Понятие «данный коллектив» — в своем обычном собирательном смысле — мы используем здесь для образования нового (общего) понятия «член данного коллектива». Это — общее, несобирательное, относительное понятие, в котором мыслится отношение людей к определенному предмету, именно к данному коллективу. Другой вид также общего и относительного понятия, представляющий собой обобщение только что рассмотренного, представляет понятие «член коллектива» (т.е. член какого-нибудь коллектива). К числу приведенных — обычно рассматриваемых делений в учебной литературе — полезно добавить деление понятий на эмпирические и теоретические. В эмпирических основное содержание составляют признаки, доступные наблюдению, например, «жидкость, не имеющая цвета, запаха и вкуса» (вода — в обыденном смысле); в теоретических понятиях наличие этих признаков у предметов устанавливается посредством некоторого теоретического анализа. Например, «химически сложное вещество, молекулы которого состоят из двух атомов водорода и одного атома кислорода» (вода — как особое химическое вещество). Еще примеры эмпирических и теоретических понятий: температура как «степень нагретости тела» в смысле ощущения его как более теплого или менее теплого (эмпирическое понятие), «величина, характеризующая физическое тело, значение которой определяется посредством термометра» (эмпирическое понятие); «характеристика физического тела, значение которой равно средней кинетической энергии движения молекул» (теоретическое понятие). Мы видели, что грани между некоторыми выделяемыми видами понятий не всегда являются достаточно четкими. Однако это не умаляет ценности этих делений (тем более, как уже подчеркивалось, во многих классификациях даже более простых объектов есть моменты условности, неопределенности, огрубления и т.д.). К тому же деление понятий на виды имеет не столько практическое, сколько теоретическое значение. Оно важно с гносеологической точки зрения, поскольку различные виды понятий представляют собой в то же время различные способы мыслительной деятельности. В многообразии видов понятий выражается активный и сложный характер отражения мира в мышлении, соответствующий сложности и многосторонности познаваемой нами действительности. Предметами понятий, как мы видели, могут быть отдельные предметы и их характеристики (свойства, отношения и т.д.). Предметы — и даже одни и те же — могут обобщаться по различным их сторонам, по наличию и отсутствию свойств, качеств, отношений, по собственным характеристикам предмета и по отношению его к другим предметам и т.д. Совокупности взаимосвязанных предметов могут мыслиться разрозненно и, наоборот, возможно мысленное объединение в некоторый агрегат предметов, существующих раздельно, и т.д. и т.п. Знание этих способов позволяет овладеть, понятием как одной из форм мышления. Это важно также и для того, чтобы умело пользоваться имеющимися в нашем распоряжении понятиями в процессе рассуждения. Упражнения Дайте характеристики следующих понятий (укажите, к каким видам они относятся): а) хвойное дерево; б) плодовое растение; в) промышленное предприятие; г) самое большое число; д) промышленное предприятие, не имеющее связей с другими предприятиями; е) социал-демократическая партия; ж) член (какой-нибудь) социал-демократической партии; з) породненные города; и) член группы какого-нибудь театра; к) население государства, расположенного на Северном полюсе; л) численность населения государства, расположенного на Южном полюсе; м) равнодействующая всех сил, действующих на Землю.
|
||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 1384; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.28.213 (0.013 с.) |

 .
. В, но обратное неверно, тогда А более информативно, чем В. А
В, но обратное неверно, тогда А более информативно, чем В. А  В само по себе указывает на то, что информация В составляет часть информации А. Обозначим объемы понятий
В само по себе указывает на то, что информация В составляет часть информации А. Обозначим объемы понятий 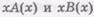 соответственно
соответственно  читается: множество предметов х, обладающих свойством А(х)). Тогда закон обратного отношения для двух понятий принимает вид: WxA(x)
читается: множество предметов х, обладающих свойством А(х)). Тогда закон обратного отношения для двух понятий принимает вид: WxA(x)  WxB(x) если и только если А(х)
WxB(x) если и только если А(х)  В(х).
В(х). , вообще, из
, вообще, из В. Предикат «х, сдавший все экзамены» информативнее, чем "х, сдавший какие-нибудь экзамены». Логическая форма первого —
В. Предикат «х, сдавший все экзамены» информативнее, чем "х, сдавший какие-нибудь экзамены». Логическая форма первого —  , второго —
, второго — 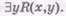 Второе есть
Второе есть ). Предикат, составляющий содержание (видовое отличие) первого понятия в формулировке парадокса Больцано имеет форму
). Предикат, составляющий содержание (видовое отличие) первого понятия в формулировке парадокса Больцано имеет форму 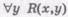 (где область значений χ — люди, у — европейские языки).
(где область значений χ — люди, у — европейские языки).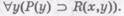 Нетрудно убедиться - что из первого логически следует второе, т.е.
Нетрудно убедиться - что из первого логически следует второе, т.е. 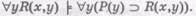

 В, то согласно законам классической логики F, А
В, то согласно законам классической логики F, А  В для любого Г. Очевидно теперь, что фактические содержания А и В упомянутых выше понятий «квадрат» и «квадрат с взаимно перпендикулярными сторонами» совпадают. Имеем Г, А
В для любого Г. Очевидно теперь, что фактические содержания А и В упомянутых выше понятий «квадрат» и «квадрат с взаимно перпендикулярными сторонами» совпадают. Имеем Г, А  Б и Г, β
Б и Г, β  А, где Г — множество из одного высказывания — теоремы геометрии: «Во всяком квадрате диагонали взаимно перпендикулярны». Аналогичным образом устанавливаем совпадение фактических содержаний понятий «число, делящееся на 2 и на 3» и «число, делящееся на 2, на 3 и на 6», используя в качестве Г множество из 3 (истинных) утверждений арифметики: «Если некоторое число а делится на β и с, которые не имеют общего делителя, отличного от единицы, то оно делится и на их произведение», «2 и 3 не имеют общего делителя, отличного от единицы», «Шесть есть произведение двух и трех».
А, где Г — множество из одного высказывания — теоремы геометрии: «Во всяком квадрате диагонали взаимно перпендикулярны». Аналогичным образом устанавливаем совпадение фактических содержаний понятий «число, делящееся на 2 и на 3» и «число, делящееся на 2, на 3 и на 6», используя в качестве Г множество из 3 (истинных) утверждений арифметики: «Если некоторое число а делится на β и с, которые не имеют общего делителя, отличного от единицы, то оно делится и на их произведение», «2 и 3 не имеют общего делителя, отличного от единицы», «Шесть есть произведение двух и трех». WxQ(x).
WxQ(x). отношения):
отношения):
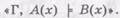 Однако допускается, что Г может быть пустым множеством (при непустом Г имеем фактические относительно этого Г объемы и содержания, при пустом — логические).
Однако допускается, что Г может быть пустым множеством (при непустом Г имеем фактические относительно этого Г объемы и содержания, при пустом — логические).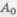 тем более информативна, чем
тем более информативна, чем  же множество
же множество  — «возможных миров», в которых истинно А. В понятии множество исходных возможностей — это его род. Объем понятия — результат его ограничения за счет добавления видового отличия. Степень этого ограничения и есть показатель информативности предиката, выражающего это видовое отличие. Закон обратного отношения играет важную роль в известных операциях обобщения и ограничения понятий и в анализе отношений между понятиями.
— «возможных миров», в которых истинно А. В понятии множество исходных возможностей — это его род. Объем понятия — результат его ограничения за счет добавления видового отличия. Степень этого ограничения и есть показатель информативности предиката, выражающего это видовое отличие. Закон обратного отношения играет важную роль в известных операциях обобщения и ограничения понятий и в анализе отношений между понятиями. Р(х)), например, «вещество, которое является кристаллическим и не является таковым». Понятие хА(х) фактически пусто, если фактически не существует предметов χ с данной характеристикой А(х). Таково, например, понятие «ворон белого цвета». Не существует также, как известно, атомов в том смысле, как их понимали в Древней Греции, а именно как неделимых частиц. Однако особый и наиболее значимый случай фактической пустоты понятия таков, когда существование предметов χ с характеристикой А(х) невозможно в силу законов той области действительности, к которой относится это понятие. Так, невозможны ромбы, в которых диагонали не являются взаимно перпендикулярными, невозможны неупругие жидкости, металлы, не обладающие хорошей электропроводимостью, и невозможны вечные двигатели (т.е. двигатели, работающие без дополнительной затраты энергии).
Р(х)), например, «вещество, которое является кристаллическим и не является таковым». Понятие хА(х) фактически пусто, если фактически не существует предметов χ с данной характеристикой А(х). Таково, например, понятие «ворон белого цвета». Не существует также, как известно, атомов в том смысле, как их понимали в Древней Греции, а именно как неделимых частиц. Однако особый и наиболее значимый случай фактической пустоты понятия таков, когда существование предметов χ с характеристикой А(х) невозможно в силу законов той области действительности, к которой относится это понятие. Так, невозможны ромбы, в которых диагонали не являются взаимно перпендикулярными, невозможны неупругие жидкости, металлы, не обладающие хорошей электропроводимостью, и невозможны вечные двигатели (т.е. двигатели, работающие без дополнительной затраты энергии). и вообще хА(х), где А(х) есть логический закон (общезначимая формула логики предикатов). Понятие фактически универсально, если предикат, составляющий его видовое отличие, не выражает никакой информации относительно предметов рода данного понятия и при этом именно в силу значений составляющих его дескриптивных терминов. Обычно это имеет место при наличии закона науки, указывающего на то, что все предметы рода обладают этим признаком. Так, например, фактически универсально понятие: «Жидкость такова, что давление на какую-нибудь ее точку передается во все стороны с одинаковой силой». Здесь мы имеем случай, когда содержанием понятия является закон-признак, необходимо присущий всем жидкостям (согласно закону Паскаля). Естественно, что он ничего не выделяет в множестве жидкостей, т.е. не несет никакой информации относительно них, поскольку верен для любых жидкостей. Но если бы в качестве родового было взято понятие «физическое тело», тогда понятие с тем же видовым отличием выделяло бы именно жидкости.
и вообще хА(х), где А(х) есть логический закон (общезначимая формула логики предикатов). Понятие фактически универсально, если предикат, составляющий его видовое отличие, не выражает никакой информации относительно предметов рода данного понятия и при этом именно в силу значений составляющих его дескриптивных терминов. Обычно это имеет место при наличии закона науки, указывающего на то, что все предметы рода обладают этим признаком. Так, например, фактически универсально понятие: «Жидкость такова, что давление на какую-нибудь ее точку передается во все стороны с одинаковой силой». Здесь мы имеем случай, когда содержанием понятия является закон-признак, необходимо присущий всем жидкостям (согласно закону Паскаля). Естественно, что он ничего не выделяет в множестве жидкостей, т.е. не несет никакой информации относительно них, поскольку верен для любых жидкостей. Но если бы в качестве родового было взято понятие «физическое тело», тогда понятие с тем же видовым отличием выделяло бы именно жидкости. универсально, и наоборот, если хА(х) универсально, то
универсально, и наоборот, если хА(х) универсально, то 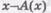 пусто.
пусто.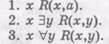
 и системы объектов (понятия вида
и системы объектов (понятия вида  Примеры первых: «живое существо», «плодовое дерево», «город, находящийся на Экваторе» и т.п. К числу вторых относятся: «параллельные прямые», «изотопы», «родственники», «супруги», «однокоренные слова», «друзья».
Примеры первых: «живое существо», «плодовое дерево», «город, находящийся на Экваторе» и т.п. К числу вторых относятся: «параллельные прямые», «изотопы», «родственники», «супруги», «однокоренные слова», «друзья». т.е. к понятиям, в которых обобщаются отдельные предметы. При этом различаются понятия конкретные и абстрактные, с одной стороны, собирательные и несобирательные — с другой. Первое из указанных делений связано с различением конкретных и абстрактных объектов1. Напомним, что конкретными объектами мы называем вещи, ситуации и процессы реальной действительности, а также результаты той или иной идеализации таких предметов (абсолютно упругие жидкости, абсолютно черные тела) и, наконец, множества и системы предметов указанных типов, мыслимые как целое.
т.е. к понятиям, в которых обобщаются отдельные предметы. При этом различаются понятия конкретные и абстрактные, с одной стороны, собирательные и несобирательные — с другой. Первое из указанных делений связано с различением конкретных и абстрактных объектов1. Напомним, что конкретными объектами мы называем вещи, ситуации и процессы реальной действительности, а также результаты той или иной идеализации таких предметов (абсолютно упругие жидкости, абсолютно черные тела) и, наконец, множества и системы предметов указанных типов, мыслимые как целое.


