
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение (дефиниция) как прием познанияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Общая характеристика определения Операция определения является одной из наиболее важных в процессе познания. Она связана с основной проблемой, определяющей роль языка как средства коммуникации и познания, а именно, — с проблемой связи выражений языка с объектами, которые эти выражения должны представлять как знаки. Другими словами, операция определения связана с проблемой формирования предметных значений знаков языка, а вместе с этим и смысловых значений выражений языка. Отсюда возникает связь рассматриваемой операции с тем, что обозначают в педагогике словами «понимание», «уяснение смысла», «сознательное усвоение учебного материала», «механическое запоминание» или злосчастная «зубрежка». Каждый, кто оглянется на свое школьное прошлое, вспомнит, вероятно, что ни одно доказательство, ни одно опровержение не обходится без определений. Наличие определений основных терминов доказательства — необходимое условие его осуществления. От наличия более или менее ясных определений терминов в том или ином изложении материала зависит ясность и точность этого изложения. К сожалению, надо заметить, что в логике и эпистемологии до сих пор не было точного и до сих пор нет общепринятого определения самого термина «определение», а это значит, не ясно, что имеется в виду под данным термином, и все разговоры в таком случае могут превратиться, по словам одного мыслителя, в «шелуху слов» вместо мыслей. Эту операцию характеризуют обычно как операцию, посредством которой раскрывается содержание понятия. Однако, как мы видели, понятие всегда характеризуется наличием какого-то содержания. «Понятие, содержание которого не раскрыто» — это просто не понятие. А если оно уже имеется, то зачем его раскрывать? При более точной трактовке определения, как приема познания, оно скорее есть способ введения понятий в науку, хотя и эта характеристика не может быть отнесена ко всем определениям вообще. Но во всяком случае здесь речь идет уже не об операциях с понятиями. Эта операция со словами, с выражениями языка. Основная цель, которой она подчинена, — обеспечение точных предметных значений слов языка как знаков. Поэтому она имеет большое значение для обеспечения определенности нашего мышления в той части, которая зависит от определенности предметных значений языковых знаков. Последние определяются как раз для того, чтобы предотвратить такие ситуации, когда знаки отрываются от их предметных значений, мышление лишается предметного содержания и превращается в пустое словотворчество. Таким образом, от определений зависит точность нашего мышления. Как метко заметил английский естествоиспытатель XIX в. Д.Гершель: «Нельзя внести точность в рассуждения, если она сначала не введена в определения».
ОПРЕДЕЛЕНИЕ есть логический способ установления или уточнения связи языкового выражения с тем, что оно обозначает как знак языка. Этот способ состоит в придании выражению некоторого смысла (или уточнении, углублении имеющегося смысла), который выделяет то, что должно быть предметным значением данного выражения. Выражение языка, к которому относится определение, называется определяемым. Знаковая форма, выражающая смысл придаваемый определяемому, называется определяющим. Определяемое иначе называют дефиниендум, а определяющее — дефиниенс. Для понимания специфики определения как приема познания полезно вспомнить основные типы языковых выражений (см. §2) и учесть, что определяемыми могут быть выражения различных синтаксических категорий: именные формы (единичные, общие имена и общие формы применения предметных функторов) и высказывательные формы (предложения и предикаты). Примеры 1. «Полярная звезда» — это та звезда, направление на которую из любой точки земного шара, с которых эта звезда видна, есть направление на север». Определяемым здесь, очевидно, является единичное имя «Полярная звезда». 2. Определение общего имени: — «Точка зенита небесной сферы — это высшая точка над головой наблюдателя». —
— «X больше у, если и только если существует такое г, что χ = у + 2» — определяемое здесь выражение — предикат (применительно к области натуральных чисел в качестве возможных значений переменных). Смысл, который приписывается в определении предложения, — это суждение или, поскольку оно выражено в определенной знаковой форме, — высказывание. Этот смысл указывает условия истинности предложения, а тем самым детерминирует (определяет) его предметное значение. Примеры определений предложений рассмотрим ниже. Сейчас заметим, что потребность в определении какого-то предложения возникает каждый раз, когда нам не ясен смысл утверждения, высказывания. Возникает, например, вопрос, что означает утверждение: «Всякое кристаллическое вещество имеет определенную температуру плавления»? Во время экзаменов, когда студенту ставят заниженную, по его мнению оценку, и он считает, что хорошо знает предмет, преподавателю нередко приходится разъяснять, что означает утверждение: «Студент хорошо знает предмет». Из приведенных примеров читателю должно быть ясно, что определяемое и определяющее выражения относятся к одной и той же синтаксической категории выражений. Точнее говоря, определяющее именно и указывает категорию того, что определяется. Кроме того, важно отметить, что определение единичных и общих имен непосредственно представляет собой способ «введения понятий в науку», поскольку, как не раз было сказано, именно понятия составляют смыслы имен — единичных и общих. По существу, это относится и к определению предикатов и к определению именной формы, ибо предикат. Возможны, по крайней мере, три типа ситуаций, в которых возникает необходимость в определении: 1. В процессе развития некоторой науки или изложения научного материала в ходе некоторой аргументации, например доказательства какой-то теоремы, вводится новая языковая форма — термин, высказывательная форма и т.п. Естественно, при этом должно быть установлено, что именно он должен представлять как знак, что имеется в виду или что хотят иметь в виду при его употреблении. Так, при описании формализованного языка логики вводят понятие терма, формулы данного языка, свободной и связанной переменной. Физик, формулируя закономерности движения, вводит термины: скорость, ускорение, траектория и т.д. Ясно, что изложение может быть понятным другому — читателю, слушателю, — если он знает, что имеется в виду под каждым выражением употребляемого языка. Поэтому введение каждого нового термина сопровождается разъяснением.
Обычно это делается в форме: «Ускорением движения в данный момент времени называют (или «будем называть») предел отношения приращения скорости в течение некоторого отрезка времени к самому этому отрезку времени при стремлении этого отрезка к нулю (т.е., говоря математическим языком, ускорение в данной точке времени есть значение — в этой точке времени — производной скорости по времени)». Впрочем, вместо «ускорением называют отношение...» может быть просто «ускорение есть отношение...», иногда с добавлением «по определению», что чаще всего просто подразумевается в силу характера контекста, в котором дается определение. Желая иметь примеры определений, читатель может вернуться хотя бы к тем частям данной работы, где разъясняются смысловые значения упомянутых выше логических терминов (терм, формула, связанная, свободная переменная и т.п.). Но каждый, вероятно, помнит многие из определений, с которыми встречался в школе: «Параллелограммом называют четырехугольник с равными противоположными сторонами», «Корень слова — это неизменяемая часть данного слова», «Остров есть часть суши, окруженная со всех сторон водой». 2. Ситуация другого типа состоит в том, что для специальных целей науки используется некоторый термин или языковый знак вообще, который имеет употребление либо в других областях знания, либо в повседневном обиходе, но при этом употребляется в различных значениях, или, наконец, в данном употреблении его хотят использовать некоторым специальным образом. Так, слово «интерпретация» употребляется весьма часто в повседневной жизни и в разных случаях ему придается различный смысл, а чаще всего никакого определенного (в силу чего расплывчатый смысл имеют и утверждения, в которых речь идет об интерпретациях, т.е. некоторых событий или каких-то выражений художественных или музыкальных произведений и т.д.). При описании формализованного языка, как мы видим, посредством определения термину «интерпретация» придан определенный смысл, а значит, и предметное значение. 3. В ситуациях третьего типа мы имеем дело с выражением, для которого уже в самой языковой практике установилось определенное, практически точное предметное значение. И задача, которую имеют в виду, применяя к такому термину определение, состоит в том, чтобы придать этому термину определенный смысл, а значит обеспечить и большую надежность и строгость в его употреблении. Так, практически каждый знает, какие существа называются словом «человек», что означает «болезнь», «производительность труда» и т.д. Однако интуитивное употребление термина оказывается недостаточным в некоторых особых ситуациях, когда нужно, например, доказать или опровергнуть утверждение, что некоторые предметы или явления относятся именно к тому классу предметов, который представляет данный термин: доказать или опровергнуть, например, что тот или иной человек действительно болен.Читатели известной книги Веркора «Люди или животные» помнят, конечно, характер показанной там ситуации, в которой жизненно важным оказалось точное решение вопроса о том, что же такое человек.
Заметим, что функции определения в ситуациях (1) и (2) существенно отличаются от той, которую она имеет в ситуации (3). В ситуациях (1) и (2) мы имеем так называемые номинальные определения. Такое определение есть условие, соглашение относительно употребления данной знаковой формы. Иначе говоря, определение в этом случае представляет собой ответ на вопрос, что имеют в виду или будут иметь в виду под данным выражением (что называют или будут называть данным термином, что мы имеем в виду, употребляя данное выражение языка). Хотя результат определения здесь и выражается в форме, сходной с повествовательным предложением, она не содержит какого-либо утверждения, кроме именно того, что данную знаковую форму предлагается употреблять так-то и так-то. Однако эта форма может быть использована в аргументации как повествовательное предложение, истинное по соглашению, именно по определению. По принципу предметности утверждение при употреблении некоторого знака относится к тому, что оно обозначает. Но в данном случае задача состоит как раз в том, чтобы установить, что именно должно обозначать определяемое выражение как знак. Существует афоризм — «Об определениях не спорят». Это относится именно к номинальным определениям. Если какой-то спор здесь и возможен, то лишь о том, целесообразно ли указанное в определении употребление термина или о том, насколько целесообразно введение самого понятия, которое ассоциируется с данным термином. Вопрос же о целесообразности введения какого-то понятия решается в связи с теми практическими и теоретическими задачами и потребностями, с которыми связано само введение термина и соответствующего ему понятия. Понятие, которое вводится посредством номинального определения термина может сохраняться при дальнейших изменениях наших знаний о предмете, при возникновении более глубоких понятий о нем, в частности, при переходе от одной теории к новой теории, возникающей в результате углубления нашего знания, с которым связано изменение реальных определений. Именно благодаря такому сохранению некоторых понятий, т.е. благодаря существованию транстеоретических понятий, создается преемственность в развитии знания. Развивая наши знания, мы не теряем из виду тех предметов, к которым относится наше познание. На них именно и указывают номинальные определения. Так при переходе от механики Ньютона к релятивистской механике изменяются понятия (наши знания) «массы», «длины», «времени» и др. Мы узнаем, например, что масса зависит от скорости — увеличивается с увеличением скорости движения тела. Однако и в той, и в другой теории мы можем иметь в виду, а ученые очевидно имеют, под термином «масса» способность тела сопротивляться изменению скорости. Определение может сохраниться даже при переходе от релятивистской к какой-то другой механике, поскольку объектом изучения будет оставаться все та же способность тел сопротивляться ускорению.
Определения в ситуации (3) называют «реальными». Другое, распространенное в литературе название этих операций — «экспликация». Результат определения такого типа представляет собой суждение — характеристику обозначаемых данным термином предметов. В силу этого здесь возникает вопрос о его истинности или ложности и, естественно, возможны споры относительно самого определения. Имеются, например, различные попытки определения «болезни», но никакое из них не является пока общепризнанным. Известны также продолжающиеся на протяжении многих веков споры о том, что такое человек. Относительно реальных определений в свою очередь имеются две возможности с точки зрения применяемых к ним требований. Иногда, ставя вопрос, например, о том, что такое человек, имеют в виду указание какой-либо отличительной совокупности признаков человека. Такому требованию удовлетворяет, очевидно, определение человека, предложенное еще в Древней Греции, как существа от природы двуногого и бесперого. Возможно также определение его как существа, обладающего способностью плакать (имея в виду эмоциональный плач, а не просто рефлекторное выделение слез, которое возможно у многих животных). Однако под реальным определением имеют в виду ответ на вопрос, что представляют собой предметы по существу, в чем состоит основа их качественной специфики? Исходя из этого, указанные определения человека не считаются удовлетворительными как реальные определения. Среди философов распространено определение человека как продукта определенной совокупности общественных отношений. Хотя сама по себе эта характеристика, будучи существенной, не является его определением, поскольку к числу людей, без сомнения, относят и Маугли. По-видимому, наиболее точным образом человек может быть определен как член сообщества, производящего и использующего в своем взаимодействии с природой орудия труда. А членом сообщества является, очевидно, каждый, кто рожден членом этого же сообщества. Из только что сказанного о реальном определении в строгом смысле ясно и то, что оно может относиться к классу предметов, уже обобщенных в том или ином понятии, но не выражающих сущность этих предметов. Есть ли, например, у нас понятие смешного? Очевидно, да. «Это все то, что вызывает смех». Но в науке нет пока ясности в том, в чем сущность смешного, каковы именно те признаки явления, в силу которых они способны вызывать смех. Говорят, что это некоторое несоответствие, но несоответствие может быть не только причиной смеха, но и слез. И остается еще задачей определить специфику несоответствия, противоречия, вынуждающих людей смеяться. Характеристика того или иного определения как номинального или реального зависит, как мы видели, от того, какую функцию или задачу оно выполняет. А это в свою очередь определяется ситуацией, в которой применяется определение. Многие номинальные определения являются таковыми для читателей и слушателей, для которых предназначено изложение некоторого научного материала, но не для самого автора. Прежде чем сообщить слушателю или читателю о том, какие предметы будет обозначать вводимый термин, автор уже имеет в виду так или иначе выделенный класс предметов и должен для себя ответить на вопрос о том, как эти предметы могут быть охарактеризованы, т.е. составить понятия о них. Это означает, что сам он вырабатывает реальные определения предметов. Виды определений По существу, мы уже выделили виды определений, различающихся по типам определяемых выражений. Кроме того, два вида определений — номинальные и реальные — уже выделены по тому, какую функцию выполняет определение, на какой вопрос оно дает ответ. Далее по структуре выделяют определения явные и неявные в зависимости от того выделяются ли в качестве самостоятельных (непересекающихся) частей определяемое выражение и определяющее. Все приведенные выше определения являлись явными. Они имеют форму равенства, если определяемым выражением является та или иная именная форма, — или эквивалентности, когда определяемое есть высказывательная форма. Отношение равенства в естественном языке обычно выражается словами «это», «есть», «это есть» или «то же, что», а эквивалентности — словосочетанием «если и только если» или «равносильно», «означает то же, что».Однако не каждое определение, имеющее форму равенства или эквивалентности является явным. Как мы увидим далее (см. контекстуальные определения), есть определения, имеющие форму равенства или эквивалентности, но не являющиеся явными. Определяемое и определяющее выражения в таких определениях не выделяются в качестве самостоятельных частей. Левая часть (равенства или эквивалентности) в них не является определяемым, а лишь содержит его в качестве своей собственной части. Явное определение — это наиболее простая и наиболее употребительная форма определений. Наличие явного определения в той или иной теории позволяет исключить (элиминировать) определяемое выражение из языка этой теории, заменяя его во всех случаях, где оно встречается, определяющей частью. Употребление его (определяемого) может быть полезно лишь ради сокращения некоторых контекстов. Принципиально оно не является необходимым. Так, вместо выражения «Полярная звезда находится в созвездии Малой медведицы» мы можем, — используя приведенное выше определение, — сказать: «Та звезда, направление на которую из любой точки земного шара, с которой эта звезда видна, есть направление на север, находится в созвездии Малой медведицы». Но ясно, что первое короче, удобнее второго. Это обстоятельство иногда истолковывают так, что само определение, имея в виду номинальное определение, можно трактовать просто как введение некоторого сокращения для определяющего выражения. Однако операцию введения сокращения надо, очевидно, отличать от определения, даже если речь идет о номинальном определении. Определение вводит в познание некоторые новые концептуальные образования. В частности, оно представляет собой способ введения понятий, что особенно важно в познании. Сокращение же предполагает уже наличие некоторого понятия (или концептуального образования вообще). Имея, например, формализованный язык с двумя логическими связками В структурах неявных определений, о которых речь ниже, нельзя выделить определяемое и определяющее в качестве самостоятельных частей, в силу чего они не дают способа элиминации определяемого из тех или иных контекстов. ВИДЫ ЯВНЫХ ОПРЕДЕЛЕНИЙ Для определений, посредством которых вводятся понятия (определения имен и предикатов), возможно выделение их видов по характеру видовых отличий этих понятий. Речь идет о характере признаков, по которым выделяется класс предметов или отдельный предмет. Такими признаками могут быть качества, свойства (в частности, свойства реляционного типа) предметов. Таковы, например, определения: «Хорда — это отрезок прямой, соединяющий две какие-нибудь точки окружности»; «Диаметр окружности — это наибольшая хорда окружности»; «Дерево — многолетнее растение, имеющее ствол, крону и корни»; «Жидкость (вещество, находящееся в жидком состоянии) — это вещество, которое имеет собственный объем, но не имеет собственной формы и принимает форму сосуда, в который помещена»; «Прибыль предприятий — это остающийся у предприятия доход после выплаты всех расходов, связанных с производством и реализацией его продукции». Наряду с такими определениями, которые можно назвать атрибутивными, выделяются генетические и операциональные. В операциональном определении видовой характеристикой предметов является указание на некоторую операцию, посредством которой эти предметы могут быть обнаружены и отличены от других предметов. Например, температуру мы можем определить как состояние предмета или среды, количественная характеристика которого может быть установлена с помощью термометра. В лингвистике операциональный характер имеют определения тех или иных выражений путем указания вопросов, на которые они отвечают, например, «существительное находится в именительном падеже, если (и только если) оно отвечает на какой-нибудь из вопросов «кто?», «что?». К этому же виду будет относиться и определение кислоты, как жидкости, окрашивающей лакмусовую бумажку в красный цвет. Весьма важным видом явных определений являются определения через абстракцию. Заметим, что этот способ применяется для определения имен таких абстрактных объектов (предметно-функциональных характеристик предметов) как: масса, форма, площадь, длина и т.п. Определение здесь осуществляется посредством особого типа отношений, называемых отношениями типа равенства (иногда — эквивалентности). Примерами таких отношений могут служить подобие (фигур), конгруэнтность отрезков: «Форма геометрической фигуры есть то общее, что имеется у всех подобных фигур». Задав отношение равновесомости двух тел, уравновешиваемости их на чашечных весах, можно определить вес как то общее, что является одинаковым у всех равновесомых предметов и различным у неравновесомых. К приведенному перечню известных видов явных определений следовало бы, как нам представляется, добавить фактически широко применяемый способ определения, который можно было бы назвать лингвистическим. Этот способ применяется для определения некоторых абстрактных объектов и состоит в том, что в качестве характеристик указываются языковые формы их выражений. Таким образом, в предыдущих частях учебника вводились понятия: «свойство», «отношение», «атрибутивное свойство», «реляционное свойство» по виду представляющих их предикатов. Напомним, что отношение, например, есть такая характеристика систем объектов, которую представляют более чем одноместные предикаты Α(χι,...,χη), а свойства — одноместные предикаты А(х). По структурам одноместных предикатов мы различаем также атрибутивные и реляционные свойства (см. §12). В лингвистике этот способ дефиниции применяется при определении частей предложения и некоторых других понятий. В заключение обзора видов явных определений отметим одну их особенность. При широком понимании свойства, как характеристики предмета, выраженной одноместным предикатом (см. §12), — очевидно, что в генетических, операциональных, лингвистических и определениях через абстракцию — во всех этих определениях в качестве видового отличия вводимого понятия указывается некоторое свойство! На этом основании, казалось бы, их можно рассматривать как виды атрибутивных... Однако при характеристике атрибутивных определений мы употребляли термин «свойство» в более узком смысле (см. §12). Учитывая это, точнее можно было бы сказать, что атрибутивное определение — это явное определение, отличающееся от всех только что перечисленных видов. Иначе говоря, атрибутивные определения — это такие определения, которые не являются лингвистическими, операциональными, генетическими и определениями через абстракцию, то есть все остальные. Обратим внимание читателя на примечательный факт. Такой способ определения «атрибутивных определений» может, вообще говоря, рассматриваться как частный случай еще одного из видов явного определения — определения посредством отрицания. Этот прием определения чаще всего применяется в случаях, когда удается определить все виды предметов некоторого класса (выделенные по одному и тому же основанию), кроме одного. Тогда предметы этого вида определяются именно как «все остальные» в данном роде. Например: «Формула является выполнимой (в узком смысле), если и только если она не является ни тождественно-ложной, ни тождественно-истинной». Надеемся, что читатель без труда может привести примеры возможных определений этого вида. Принимая во внимание еще один вид явных определений — только что рассмотренный — и возвращаясь к определению атрибутивных дефиниций, мы должны из класса «остальных» исключить, конечно, и определения посредством отрицания. ВИДЫ НЕЯВНЫХ ОПРЕДЕЛЕНИЙ Вспомним сказанное выше о том, что неявные определения отличаются от явных тем, что в них нельзя выделить в качестве самостоятельных частей определяемое и определяющее выражения и, значит, нельзя представить в виде равенства или эквивалентности, левая часть которых представляла бы определяемое выражение. Однако, как мы уже говорили, есть вид неявных определений — контекстуальные определения, — которые имеют вид равенства или эквивалентности. Тем не менее левая часть этого равенства есть не определяемое, а некоторый контекст, в частности, — возможно предложение, включающее определяемое как некоторую свою правильную часть. Таким — неявным — образом определяются, например, выражения, образуемые посредством определенной и неопределенной дескрипций (
Пример Предложение «То небесное тело, которое является естественным спутником Земли, есть остывшее тело» истинно, если и только если существует небесное тело, которое является естественным спутником Земли и является остывшим, и для любого тела, которое является естественным спутником Земли, верно, что оно совпадает с упомянутым (х)» «. Итак, форма определения здесь есть эквивалентность. Однако читатель должен увидеть, что левая ее часть — Определения такого — неявного — вида всегда можно рассматривать как явное определение всего выражения, стоящего в левой части, в данном случае — предложения. Точнее говоря, оно представляет собой схему определений любых предложений указанной структуры. Таким образом, одно и то же определение может быть явным относительно одного выражения и неявным контекстуальным относительно термина «необходимо». В приведенных ранее таблицах, выражающих условия истинности высказываний, образованных посредством операций В традиционных учебниках по логике контекстуальным определением некоторого термина называют обычно разъяснение его смысла и предметного значения посредством указания совокупности предложений или высказываний, содержащих этот термин. Такими совокупностями, по мнению многих авторов, могут быть совокупности аксиом некоторой математической теории, совокупность уравнений и т.п. Более того, имеется мнение, что всякая совокупность слов, всякий контекст, в котором встречается интересующее нас выражение, является неявным его определением. Однако это, очевидно, не так. Определяет ли смысл (и соответственно предметное значение) слова «дядя» следующий известный пушкинский контекст? Мой дядя самых честных правил, Когда не в шутку занемог, Он уважать себя заставил И лучше выдумать не мог. В современной логике выяснено, что далеко не всякая совокупность предложений, в которых содержится некоторый термин, является его неявным определением. Установлен точный критерий, в каких случаях имеет место неявная определимость, например, некоторого предикатора Ρ множеством содержащих его предложений I1. Используя этот критерий, можно, конечно, говорить, что в соответствующих — положительных — случаях мы имеем неявное определение термина. Однако речь здесь идет об определении не как об особой логической операции, а как о некоторой характеристике контекста, его отношении к термину. Другим важным видом неявных определений являются индуктивные определения («определения по индукции»). С определением этого вида мы уже имели дело при определении формул ЯЛВ и ЯЛП, термов в ЯЛП. Эта форма неявного определения применяется для определения общих имен и является таким образом специфическим способом введения понятий в науку. Она применяется в тех случаях, когда класс-объем определяющего понятия может быть разделен на две части: 1) совокупность некоторых элементарных объектов этого класса и 2) совокупность объектов, которые могут быть построены из других объектов этого же класса, а в конечном счете — из элементарных, посредством некоторых операций. Рекомендуем читателю обратиться к упомянутым только что определениям и проанализировать их с точки зрения данного здесь их описания. Дополнительно к этим определениям укажем известное определение термина «натуральное число». Элементарным объектом класса натуральных чисел является 0 (ноль). А операцией, посредством которой любое натуральное число (кроме 0) может быть образовано из другого, и в конечном счете из 0, является прибавление единицы, или, как иначе говорят еще, операция образования объема, «следующего за га» (для обозначения объекта, «следующего за га» принято обозначение «га'»). Все определение термина «натуральное число» выглядит так: 1. 0 есть натуральное число. 2. Ничто другое, кроме указанного в пунктах 1 и 2, не есть натуральное число. Следует обратить внимание на специфику индуктивных определений, состоящую в том, что определяемое выражение используется здесь в определяющей части. Это создает видимость известной ошибки в определениях «порочного круга», но «круг» фактически «разрывается» благодаря именно расслоению класса предметов на некоторые уровни (известно, что до открытия индуктивных определений логикой в науке возникали в определенных случаях трудности, связанные как раз с неумением выйти из кажущегося «порочного круга», по видимости, неизбежно возникающего в некоторых случаях). Среди неявных определений также можно выделить виды генетических и операциональных. Так, индуктивное определение, по существу, является генетическим, поскольку основная его часть состоит в указании способа построения объектов из других и в конечном счете — из элементарных. Таким образом, есть виды явных операциональных и генетических, а также и неявных определений этого типа. Известен, кроме рассмотренных выше, еще один вид неявных определений — рекурсивные определения. В этих определениях задаются операции вычисления значений предметных функторов, т.е. вычисление возможных значений форм имен вида: «х+y», "x-y" и т.д. Широкое применение этот вид определения находит в математике и математической логике. В заключение данного параграфа обращаем внимание читателя на то, что в учебниках традиционной логики среди явных определений в качестве особого вида выделяют обычно так называемые определения «через род и видовое отличие». При этом имеется в виду, что в определяющей части этих определений указывается некоторый класс предметов («род») и видовое отличие, посредством которого в этом классе выделяется определяемый класс предметов. Например, «Ромб есть плоский, замкнутый четырехугольник (род), все стороны которого равны (видовое отличие)». Однако мы видели уже, что всякое понятие представляет собой результат обобщения предметов некоторого класса и мысленного выделения его в пределах более широкого класса. То есть понятие всегда имеет родо-видовую структуру. Таким образом, определение «через род и видовое отличие» — это просто определение общего или единичного имени, посредством которого вводится некоторое понятие. Это значит, что, в частности, индуктивное определение есть тоже определение через род и видовое отличие. Более того, указание рода необходимо во многих других видах определений. Например, при определении выражения типа А(х) (одноместного предиката) необходимо указание области значений х. Аналогично дело обстоит и при определении предметных функторов. Следовательно, определение «через род и видовое отличие» не является особым видом определения.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.177.204 (0.015 с.) |

 — это число, равное отношению длины катета, противолежащего углу х, к гипотенузе прямоугольного треугольника» (где область D для χ — множество острых углов прямоугольного треугольника) — определяемое здесь, очевидно, — общая форма применения предметного функтора «синус». Это определение отличается от определения «sin», представляющего имя функции, которую (опять-таки применительно к множеству острых углов прямоугольных треугольников) можно определить как «функцию, которая соотносит каждому углу (из указанной области) число, равное отношению длины соответствующего катета к длине гипотенузы».
— это число, равное отношению длины катета, противолежащего углу х, к гипотенузе прямоугольного треугольника» (где область D для χ — множество острых углов прямоугольного треугольника) — определяемое здесь, очевидно, — общая форма применения предметного функтора «синус». Это определение отличается от определения «sin», представляющего имя функции, которую (опять-таки применительно к множеству острых углов прямоугольных треугольников) можно определить как «функцию, которая соотносит каждому углу (из указанной области) число, равное отношению длины соответствующего катета к длине гипотенузы».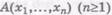 , который здесь приписывается в качестве смысла, представляет собой содержание понятия вида
, который здесь приписывается в качестве смысла, представляет собой содержание понятия вида  . А выражение
. А выражение  — составляющее смысл, приписываемый именной форме - - является существенной частью содержания понятийной формы вида
— составляющее смысл, приписываемый именной форме - - является существенной частью содержания понятийной формы вида 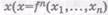 ) (число х, равное
) (число х, равное  ). Ясно, что при определенных значениях
). Ясно, что при определенных значениях  эта понятийная форма превращается в понятие. «Определить некоторое выражение» буквально (например, в польском языке) означает «определить», т.е. установить границы его применения. Однако, поскольку в определении мы приписываем смысл термину, то тем самым характеризуем предметы, т.е. определяем предметы. Более того, под определением термина мы имеем в виду именно указание характеристик предметов, которые он обозначает или должен обозначать. Определяя квадрат, мы характеризуем его как равносторонний прямоугольник. Но определяя термин «квадрат» в буквальном смысле, мы должны были бы сказать, что это есть слово, служащее для обозначения равносторонних прямоугольников.
эта понятийная форма превращается в понятие. «Определить некоторое выражение» буквально (например, в польском языке) означает «определить», т.е. установить границы его применения. Однако, поскольку в определении мы приписываем смысл термину, то тем самым характеризуем предметы, т.е. определяем предметы. Более того, под определением термина мы имеем в виду именно указание характеристик предметов, которые он обозначает или должен обозначать. Определяя квадрат, мы характеризуем его как равносторонний прямоугольник. Но определяя термин «квадрат» в буквальном смысле, мы должны были бы сказать, что это есть слово, служащее для обозначения равносторонних прямоугольников. (материальной импликацией и отрицанием), можно ввести по определению высказывание вида
(материальной импликацией и отрицанием), можно ввести по определению высказывание вида  (А или В):
(А или В):  . Но явно другой смысл будет иметь соглашение: «Используем для Λ
. Но явно другой смысл будет иметь соглашение: «Используем для Λ  В сокращение
В сокращение 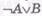 ". (О соотношении понятий и сокращений для них см.§16.)
". (О соотношении понятий и сокращений для них см.§16.) —, а именно: непосредственно определяются при этом предложения вида
—, а именно: непосредственно определяются при этом предложения вида  ). Определения их мы уже имели. Напомним их здесь.
). Определения их мы уже имели. Напомним их здесь. . («Существует предмет χ (из области D), который обладает свойством АиВ и притом он является единственным, обладающим свойством А».)
. («Существует предмет χ (из области D), который обладает свойством АиВ и притом он является единственным, обладающим свойством А».)
 ) и
) и 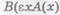 ) — содержит определяемое (соответственно:
) — содержит определяемое (соответственно:  и
и 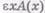 ) как свою правильную — не совпадающую с целым — часть. В правой же — определяющей — части это выражение уже не содержится.
) как свою правильную — не совпадающую с целым — часть. В правой же — определяющей — части это выражение уже не содержится.
 мы имеем явные определения соответствующих высказываний и неявные контекстуальные определения указанных операций как функторов. Например, табличное определение высказывания «р&q» в развернутой форме может быть представлено так: высказывание вида р&q эквивалентно (по определению) такому высказыванию, которое имеет истинностные значения, указанные в таблице (см. §9). Но здесь же мы имеем неявное (контекстуальное определение самого функтора «&», как операции, посредством которой образуются высказывания рассматриваемого вида).
мы имеем явные определения соответствующих высказываний и неявные контекстуальные определения указанных операций как функторов. Например, табличное определение высказывания «р&q» в развернутой форме может быть представлено так: высказывание вида р&q эквивалентно (по определению) такому высказыванию, которое имеет истинностные значения, указанные в таблице (см. §9). Но здесь же мы имеем неявное (контекстуальное определение самого функтора «&», как операции, посредством которой образуются высказывания рассматриваемого вида).


