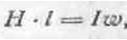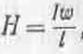Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особливості фізичних процесів в магнітних ланцюгах змінного струмуСодержание книги
Поиск на нашем сайте
При аналізі магнітних ланцюгів змінного струму вводять наступні допущення: 1) магнітне поле розсіяння відсутнє; 2) активний опір обмотки рівний нулю. При таких допущеннях можна записати
де
Звідси витікає, що магнітний потік в магнітопроводі змінний і визначається напругою (дією)
Таким чином, закон зміни магнітного потоку Ф(t) не залежить від параметрів ланцюга. Це перша особливість магнітних ланцюгів змінного струму. Щоб визначити другу особливість звернемося до відомого виразу
З нього виходить, що
Але для простого магнітного ланцюга справедливі рівняння:
Змінні В(t) і Н(t) зв'язані за законом динамічної петлі гістерезису. Цей зв'язок нелінійний. Тобто залежність (22) теж нелінійна, а індуктивність Це друга особливість. Індуктивність обмотки магнітопроводу непостійна і залежить від струму ланцюга, а рівняння Звідси третя особливість: магнітні ланцюги є нелінійними ланцюгами, тому при синусоїдальній напрузі на обмотці струм в ній опиняється не синусоїдальним. Зміна магнітного потоку Ф(t) з частотою Закон повного току На рис. 9 показаний провідник із струмом I, пронизливий поверхню, обмежену замкнутим контуром у вигляді кола. Хай центр кола лежить на осі провідника. У просторі, що оточує провідник із струмом, виникає магнітне поле. Оскільки окремі точки контуру знаходяться від провідника на рівних відстанях, то напруженість поля, створена струмом в кожній точці контуру, буде також однаковою. Напрям вектора напруженості поля R залежить від напряму струму в провіднику і визначається за «правилом буравчика». Вектор H розташовується по дотичній до кола контуру. Шляхом дослідів і розрахунків встановлено, що добуток напруженості поля Н в точках контуру на довжину цього контуру L рівний струму I, що пронизує поверхню, обмежену даним контуром.
Таким чином
У загальному випадку поверхню можуть пронизувати декілька струмів. Тоді визначають так званий повний струм, тобто знаходять алгебраїчну суму струмів
Для цього випадку можна записати:
Цей вираз носить назва закону повного струму Закон повного струму є основним законом при розрахунку магнітних ланцюгів і дає можливість в деяких випадках легко визначити напруженість поля. Наприклад, застосувавши закон повного струму для визначення напруженості магнітного поля в точці на відстані r від нескінченно довгого прямолінійного провідника із струмом (рис. 9), маємо наступне: повний струм дорівнює струму в провіднику
Переходячи до магнітної індукції, матимемо
Площу контуру пронизує повний струм, рівний добутку струму I на число витків W котушки, тобто Позначивши довжину осі котушки через L, запишемо закон повного струму:
звідки
або, переходячи до магнітної індукції, матимемо
Якщо перетин кільцевої котушки позначити S, то магнітний потік, що проходить усередині котушки, буде
Розрізавши кільце і випрямивши котушку, ми отримаємо соленоїд. Для соленоїда нескінченно великої довжини формули для напруженості поля R по осі соленоїда, магнітній індукції В і магнітного потоку Ф ті ж, що і для кільцевої котушки. Проте на практиці, маючи справу з соленоїдами обмеженої довжини, для визначення R, В і Ф користуються тими ж формулами.
|
|||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.173.208 (0.008 с.) |





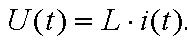



 змінна.
змінна. нелінійно.
нелінійно. приводить до нагріву магнітопроводу із-за гістерезису. Отже, в магнітопроводі виникають втрати електроенергії. Їх називають магнітними втратами. Це четверта особливість.
приводить до нагріву магнітопроводу із-за гістерезису. Отже, в магнітопроводі виникають втрати електроенергії. Їх називають магнітними втратами. Це четверта особливість.



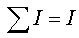 ; контур, проведений на відстані r від провідника, співпадає з магнітною лінією; довжина контуру L буде L=2рr, тому
; контур, проведений на відстані r від провідника, співпадає з магнітною лінією; довжина контуру L буде L=2рr, тому  , звідки
, звідки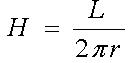
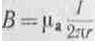 , тобто ми отримали той же вираз для магнітної індукції, який було приведено вище для такого ж випадку. Застосуємо закон повного струму для визначення напруженості поля по осі котушки, рівномірно намотаної на кільце (рис. 10). контуром тут є вісь котушки (вона ж вісь кільця).
, тобто ми отримали той же вираз для магнітної індукції, який було приведено вище для такого ж випадку. Застосуємо закон повного струму для визначення напруженості поля по осі котушки, рівномірно намотаної на кільце (рис. 10). контуром тут є вісь котушки (вона ж вісь кільця).