Булеві функції (функції логіки)
Содержание книги
- Джерела винекнення електрики
- Електрорушійна сила та напруга джерела струму
- Поняття електричного ланцюга
- Основні топологічні поняття і визначення теорії електричних ланцюгів
- Складні ланцюги постійного струму
- Закони Ома і кірхгофа в комплексній формі.
- Послідовне та паралельне з'єднання резистивного, індуктивного та ємкісного елементів.
- Активна, реактивна, повна потужність
- Послідовний коливальний контур. Pезонанс струмів
- Властивості феромагнітних матеріалів.
- Особливості фізичних процесів в магнітних ланцюгах змінного струму
- Котушка індуктивності в ланцюзі змінного струму.
- Величина струму прямо пропорційна напрузі і обернено пропорційна індуктивному опору ланцюгу,
- Принцип роботи трансформатора.
- Режими роботи трансформатора.
- Робота трансформатора під навантаженням.
- Причини виникнення перехідних процесів.
- Періодичний (що коливається) розряд конденсатора на ланцюг з резистором і котушкою
- Що відбувається при перемиканні із зірки в трикутник і назад в найбільш поширених випадках .
- Пакет моделювання Electronics Workbench
- Основні прийоми роботи з пакетом EWB
- Зовнішній інтерфейс користувача Electronics Workbench
- Моделювання RC – ланцюга, що інтегрує
- Моделювання RC – ланцюга, що диференціює
- Схема алгебраїчного суматора
- Потужність втрат на внутрішньому опорі джерела
- Розрахунок ланцюга з одним джерелом живлення
- Складемо і вирішимо системи рівнянь.
- Як експериментально визначити параметри еквівалентного генератора ?
- Електричні ланцюги постійного струму і методи їх розрахунку
- Аналогічно поступаємо з другим індикатором напруги
- Моделюємо виміри значення струму на резисторі R1
- Класифікація напівпровідникових електронних приладів
- Така домішка називається донорською, провідність – електронною, а напівпровідник – напівпровідником n – типу.
- Принцип роботи каскаду по схемі із загальним емітером
- Отже, сигнал – змінна фізична величина, що забезпечує передачу інформації лінією зв'язку.
- Тригери та їхні характеристики
- Загальні відомості про цифрові сигнали
- Булеві функції (функції логіки)
- Дискретні (цифрові) автомати
- Постійні запам’ятовуючі пристрої (ПЗП).
- Класифікація електронних систем
- Поняття про цифровий вимірювальний прилад
- Роль програмованих великих інтегральних схем у створенні сучасної електронної апаратури
- Загальна структурна схема ПЛІС.
- Непозиційна система числення
- Де і в якому віку виготовлена судина ?
- Використання алгебри логіки до релейно-контактних схем
- Моделювання інтегруючого RC – ланцюга
Результат виконання логічних операцій над двійковими змінними називається булевою функцією F. Вона може приймати тільки два значення – " 0 " або " 1 ". Задати булеву функцію – означає вказати її значення при всіх можливих комбінаціях змінних (аргументів). Якщо число змінних рівне " n ", то число можливих комбінацій рівне 2n. Коли значення функції відоме для всіх комбінацій, вона називається повністю визначеною. Інакше – частково визначеною.
Булеві функції необхідні для синтезу цифрових пристроїв, що містять тільки логічні елементи. Для представлення булевих функцій часто застосовують словесний опис, табличне і алгебру уявлення.
Словесний опис функції повинен однозначно визначати всі випадки, в яких вихідні сигнали приймають значення " 1 " або " 0 ". Наприклад: Спроектувати пристрій з трьома входами x1, x2, x3, на виході якого сигнал F = 1 у випадку, якщо на будь-яких два або на всі три входи поданий сигнал " 1 ".
Табличне уявлення – це перерахування всіх можливих комбінацій вхідних сигналів. Для пристрою, заданого приведеним вище словесним описом, таблиця значень має вигляд
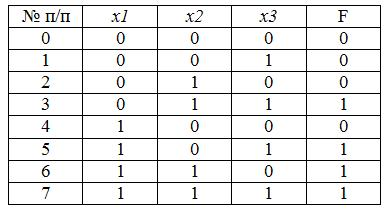
Tаблиця істинності
Форма алгебраїчного представлення булевих функцій використовується для мінімізації (спрощення формул) і для побудови логічних схем. Існує дві форми алгебраїчних функцій – диз'юнктивна і кон'юнктивна. Диз'юнктивна нормальна форма є сумою елементарних добутків аргументів, наприклад

Форм. 23
Якщо кожен доданок містить всі аргументи або їх заперечення, то отримуємо досконалу диз'юнктивну нормальну форму (ДДНФ), наприклад

Форм. 24
Досконала кон'юнктивна нормальна форма (ДКНФ) є логічним добутком елементарних логічних сум, причому кожна сума містить всі аргументи або їх заперечення, наприклад

Форм. 25
Для переходу від таблиці істинності до ДДНФ враховуються тільки ті стани, для яких функція рівна 1. Для кожного такого стану записується елементарний добутокр всіх аргументів. Якщо аргумент має значення " 0 ", то записується його заперечення. Для приведеного прикладу ДДНФ має вигляд
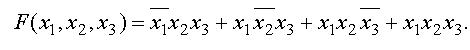
Форм. 26
Для переходу від таблиці істинності до ДКНФ враховуються тільки ті стани, для яких функція рівна " 0 ". Для кожного такого стану записується елементарна сума аргументів. Якщо аргумент має значення " 1 ", то пишеться його заперечення. Для приведеного прикладу ДКНФ має вигляд

Форм. 27
На підставі отриманих формул (26) або (27) можна побудувати логічну схему, що складається з елементів "АБО", "І", "НІ". Для функції (26) спочатку зображаються інвертори, потім осередки " І " і потім осередки " АБО " (рис. 7).

Рис. 7
Схеми рис. 7 і рис. 8 містять всі типи логічних елементів. У зв'язку з цим створені логічні елементи, здатні виконати просту функцію двох аргументів " АБО-НІ ", а також " І-НІ ". За допомогою кожного з цих елементів можна виразити всі основні операції булевої алгебри, а значить реалізувати будь-яку логічну функцію.

Рис. 8
|