
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Активна, реактивна, повна потужністьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для аналізу (64) застосуємо відомі з курсу тригонометрії формули перетворення:
Застосовуючи їх до (64) отримаємо:
де I - значення струму, що діє, причому Перші два доданки в (66) визначають миттєву потужність, що виділяється на елементі R. Можна записати, що
Як видно з (67) миттєва потужність РR(t) містить постійну складову Р = RI2 та змінну складову, що змінюється з подвоєною частотою. Графік РR(t) приведений на рис. 10.
Графік наочно показує, що потужність РR(t) завжди позитивна і змінюється від 0 (у момент Середнє за період значення потужності позначають Р і називають aктивною потужністю, причому
Для детальнішого аналізу миттєвої потужності Рr(t) звернемося до виразу (63). Цьому виразу відповідає векторна діаграма рис. 11. У ній як початковий прийнятий вектор струму
Проведемо додавання векторів. Для цього початок вектору Результатом додавання є вектор Кут З'єднаємо точки кінців двох векторів -
Повернемося знов до аналізу миттєвої потужності, що виділяється на елементі R, - Рr(t). З врахуванням (69) перепишемо (67) у вигляді
Перший вираз в правій частині повністю відповідає (68) тобто визначає активну потужність
Вираз (74) використовується в практиці набагато частіше оскільки визначає залежність активної потужності від зміщення фаз між значеннями струму і напруги ланцюга, що діють. Через це коефіцієнт
Звернемося до початкового виразу для миттєвої потужності ланцюга - (66). У ньому третій і четвертий вираз визначають потужність, що виділяється на реактивних елементах – індуктивності
і ємкості
Кожен з цих виразів змінюються з подвоєною (щодо струму) частотою, але мають протилежні фази (рис.12).
Оскільки постійна складова в (76) і (77) відсутні, то середнє значення кожного з них рівна нулю. Проте сума РL(t) і РC(t) відмінна від нуля і визначає миттєву потужність реактивних елементів (ділянок) ланцюга. Визначимо її:
Застосуємо до (78), (76), тоді
Коефіцієнт
називається реактивною потужністю, позначається Q і вимірюється у вольт-амперах реактивних [вар]. Тепер загальний вираз для миттєвої потужності всього ланцюга можна записати у вигляді
Другий і третій вирази у (4.22) згорнемо як косинус суми аргументів -
Таким чином, миттєва потужність ланцюга має постійну і змінну складові. Змінна складова змінюється щодо постійної з подвоєною частотою (рис. 13). Амплітудне значення змінної складової позначають S і називають повною потужністю ланцюга
Повна потужність у Якщо помножити всі сторони трикутника опорів на I2 то отримаємо трикутник потужностей (рис.14). У цьому трикутнику гіпотенуза - повна потужність S, прилеглий до гострого кута катет - активна потужність Р, а протилежний катет - реактивна потужність Q.
Кут
Повна потужність S це теоретично досяжна, розрахункова потужність, За значенням S проводяться розрахунки перетину проводів, ізоляція, параметри приймачів електричної енергії. Із-за зміщення фаз
|
||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 465; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.20.205 (0.007 с.) |



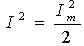


 ; до 2RI2 (у моменти
; до 2RI2 (у моменти  період струму.
період струму.
 . Вектор напруги на індуктивності
. Вектор напруги на індуктивності 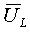 випереджає струм, а на ємкості
випереджає струм, а на ємкості 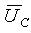 відстає від струму на 90о. Напруга на резисторі
відстає від струму на 90о. Напруга на резисторі  співпадає по фазі із струмом.
співпадає по фазі із струмом.
 , який виходить з початку вектора
, який виходить з початку вектора 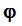 визначає зміщення фаз між током та напругою отриманою у результаті, тобто
визначає зміщення фаз між током та напругою отриманою у результаті, тобто 
 Позначимо знов отриманий вектор
Позначимо знов отриманий вектор  Трикутник, що утворився, з векторів
Трикутник, що утворився, з векторів  називають трикутником напруги. Для нього справедливі наступні вирази:
називають трикутником напруги. Для нього справедливі наступні вирази:

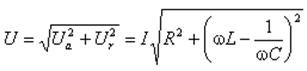


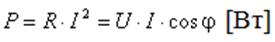
 називають коефіцієнтом потужності і позначають
називають коефіцієнтом потужності і позначають 





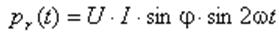


 Тоді
Тоді


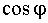 раз перевищує постійну складову (активну потужність). Тому графік миттєвої потужності заходить в область негативних значень. Величина області негативних значень визначається коефіцієнтом потужності. Фізично ця область визначає моменти часу в яких ланцюг повертає енергію джерела.
раз перевищує постійну складову (активну потужність). Тому графік миттєвої потужності заходить в область негативних значень. Величина області негативних значень визначається коефіцієнтом потужності. Фізично ця область визначає моменти часу в яких ланцюг повертає енергію джерела.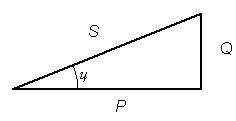
 визначається зміщенням фаз між струмом і напругою ланцюга і задає значення коефіцієнта потужності. Для трикутника очевидні вирази
визначається зміщенням фаз між струмом і напругою ланцюга і задає значення коефіцієнта потужності. Для трикутника очевидні вирази





