
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точка перетину прямої з площиноюСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Якщо пряма
Це зручніше зробити, якщо рівняння
і підставити ці вирази в рівняння
За знайденим значенням Приклади 1.Знайти точку перетину прямої Розв’язання. Запишемо рівняння прямої в параметричному вигляді:
2. Знайти точку N симетричну з точкою М(-1,4,2) відносно площини Розв’язання. Спочатку складемо рівняння прямої, яка проходить через точку М(-1,4,2) перпендикулярно до площини. За напрямний вектор Знайдемо точку перетину знайденої прямої з площиною. З рівняння прямої виражаємо
Отже, симетричною з точкою М(-1,4,2) відносно заданої площини є точка N(5,6,4).
Задачі для самостійного розв’язання 1. Довести, що пряма 2. Знайти точку перетину прямої 3. Скласти рівняння площини, яка проходить через точку А(-2,3,3) і перпендикулярна прямій 4. Через точку М0(1,-3,5) провести пряму, перпендикулярно до площини 5. Знайти координати основи перпендикуляра, опущеного з точки М(5,0,8) на площину 6. Знайти точку А1 симетричну з точкою А(7,5,-8) відносно площини 7. Довести, що прямі 8. Довести, що прямі 9. Знайти точку А1, яка симетрична з точкою А(4,-2,1) відносно прямої 10. Дано дві мимобіжні прямі: Вказівка. 1) Знайти вектор Відповіді: 2.
Криві другого порядку
Рівняння вигляду
де хоча б один з коефіцієнтів Рівняння (35) завжди описує пряму лінію. Алгебраїчним рівнянням другого порядку називається всяке рівняння вигляду
де хоча б один з коефіцієнтів Лінії, координати точок яких задовольняють рівняння (36) називаються лініями другого порядку. До ліній другого порядку відносяться: еліпс (зокрема коло), гіпербола, парабола. Вони описуються рівнянням вигляду (36). Однак не кожне рівняння другого порядку завжди описує одну із згаданих ліній. Може, наприклад, вийти так, що рівняння вигляду (36) описує пару прямих ліній або не визначає жодного реального об’єкту.
Приклади. 1. Рівняння 2. Рівняння 3. Рівняння 4. Рівняння 5. Рівняння 6. Рівняння 7. Рівняння Додамо ще, що при відповідному виборі декартової системи координат рівняння (36) для кривих другого порядку набувають простий, так званий канонічний вигляд. Далі розглянемо коротко кожну із кривих другого порядку.
Коло
Означення. Колом називається множина точок Нехай
– рівняння кола радіуса Якщо ж центр кола збігається з початком координат,
-канонічне рівняння кола. Розкриємо дужки в (37) і зведемо його до вигляду (36)
Отже загальне рівняння (36) може описувати коло, якщо
Приклад. Знайти центр кола і радіус, якщо 1. Розв’язання. Згрупуємо відносно
Отже, центр кола в точці
2. Розв’язання.
Сумма квадратів в лівій частині рівності не може бути від’ємною. Дане рівняння не описує кола.
|
||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 1060; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.192.2 (0.008 с.) |

 не паралельна площині
не паралельна площині  , то вони перетинаються в одній точці. Щоб знайти точку перетину необхідно розв’язати систему їх рівнянь
, то вони перетинаються в одній точці. Щоб знайти точку перетину необхідно розв’язати систему їх рівнянь
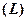 записати в параметричній формі
записати в параметричній формі
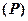 , тоді одержимо
, тоді одержимо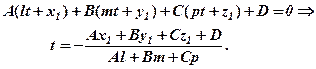
 із (34) знаходимо координати
із (34) знаходимо координати  точки перетину.
точки перетину. з площиною
з площиною  .
. Підставимо вирази для x, y, z в загальне рівняння площини
Підставимо вирази для x, y, z в загальне рівняння площини Звідки
Звідки 

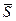 можна взяти нормальний вектор
можна взяти нормальний вектор  даної площини (див. умову (33) попереднього параграфа
даної площини (див. умову (33) попереднього параграфа  ). Отже, маємо
). Отже, маємо 
 і підставляємо у рівняння площини
і підставляємо у рівняння площини
 – точка перетину прямої і площини. Ця точка є серединою між двома симетричними відносно площини точками М(-1,4,2) і N(XN, YN, ZN), тобто
– точка перетину прямої і площини. Ця точка є серединою між двома симетричними відносно площини точками М(-1,4,2) і N(XN, YN, ZN), тобто

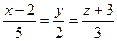 паралельна площині
паралельна площині  а пряма
а пряма  перпендикулярна цій площині.
перпендикулярна цій площині. з площиною, яка проходить через точку М(0,3,-5), перпендикулярно до цієї прямої.
з площиною, яка проходить через точку М(0,3,-5), перпендикулярно до цієї прямої.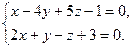


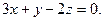
 та
та 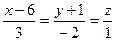 перетинаються, та скласти рівняння площини, на якій вони лежать.
перетинаються, та скласти рівняння площини, на якій вони лежать.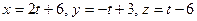 і
і  паралельні, та знайти рівняння площини, в якій вони лежать.
паралельні, та знайти рівняння площини, в якій вони лежать.
 і
і 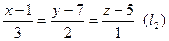 . Необхідно: 1) скласти рівняння площини, яка проходить через пряму
. Необхідно: 1) скласти рівняння площини, яка проходить через пряму  1 і паралельна прямій
1 і паралельна прямій  Рівняння площини знаходиться за точкою М1(6,-1,0) та нормальним вектором
Рівняння площини знаходиться за точкою М1(6,-1,0) та нормальним вектором 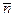 . 2) Відстань між прямими збігається з відстанню від точки М2(1,7,5) до знайденої в п. 1) площини.
. 2) Відстань між прямими збігається з відстанню від точки М2(1,7,5) до знайденої в п. 1) площини. 3.
3. 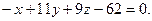 4.
4.  5.
5. 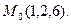 6.
6. 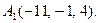 7.
7. 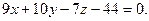 8.
8.  9.
9. 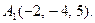 10.
10. 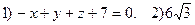 .
.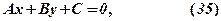
 або
або  відмінний від нуля, називається алгебраїчним рівнянням першого порядку, або першого степеня відносно змінних
відмінний від нуля, називається алгебраїчним рівнянням першого порядку, або першого степеня відносно змінних  і
і  .
.
 .
. описує коло.
описує коло. описує параболу.
описує параболу.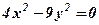 розпадається на дві прямі
розпадається на дві прямі  і
і  , що перетинаються.
, що перетинаються. , тобто
, тобто  розпадаються на дві паралельні прямі
розпадаються на дві паралельні прямі 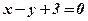 і
і 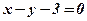 .
. , тобто
, тобто 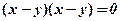 розпадається на дві прямі, що збігаються.
розпадається на дві прямі, що збігаються. має своїм розв’язком тільки одну точку
має своїм розв’язком тільки одну точку  .
. не описує в області дійсних чисел ніякого геометричного місця точок.
не описує в області дійсних чисел ніякого геометричного місця точок. площини, які знаходяться на відстані R від заданої точки
площини, які знаходяться на відстані R від заданої точки  .
. – центр кола,
– центр кола,  – довільна точка кола. За умовою
– довільна точка кола. За умовою  , а за формулою відстані між двома точками маємо
, а за формулою відстані між двома точками маємо
 з центром в точці
з центром в точці  , то отримуємо
, то отримуємо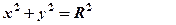
 .
. а
а 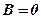 . За цих умов, щоб знайти центр кола і його радіус, потрібно виділити повний квадрат.
. За цих умов, щоб знайти центр кола і його радіус, потрібно виділити повний квадрат.

 , а радіус
, а радіус  . Пропонуємо побудувати це коло.
. Пропонуємо побудувати це коло.




