
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівняння площини за трьома точкамиСодержание книги
Поиск на нашем сайте
Нехай задані три точки компланарні, тобто коли їх мішаний добуток В координатній формі запишеться:
– рівняння площини за трьома точками. Приклад. Скласти рівняння та побудувати площину, яка проходить через точки Розв’язання. За формулою (20)
площина паралельна
Рис. 19.
3.13. Кут між двома площинами. Умова паралельності та перпендикулярності площин
Якщо для однозначності кутом між двома площинами називати один з менших двогранних кутів між ними, а відповідно до цього менший із кутів назвемо кутом між двома векторами, то кут між двома площинами є кутом між їх нормальними векторами (див. рис. 20),
Рис. 20.
де
Якщо
– умова перпендикулярності двох площин. Коли ж
– умову паралельності двох площин.
Відстань від точки до площини
Відстань
Дійсно, із рисунка 21
Рис. 21.
бачимо, що для довільної точки
де
бо із Задачі для самостійного розв’язання 1. Дано точки 2. Знайти точку перетину трьох площин
Вказівка. Розв’язати систему рівнянь.
3. Побудувати площини: 1) 4. Скласти рівняння площини, яка перпендикулярна осі ОУ і проходить через точку М(-6,7,10). 5. Написати рівняння площини, яка проходить через вісь ОХ і точку М(4,-5,6). 6. Написати рівняння площини, яка паралельна осі OZ і проходить через точки М(-1,4,-8) і N(2,-3,-1). 7. Записати рівняння площини 8. Знайти об’єм піраміди, утвореної координатними площинами та площиною 9. Дано площину 10. Дві грані куба лежать на площинах 11. Скласти рівняння геометричного місця точок, рівновіддалених від двох площин 12. Знайти гострий кут між площинами 13. Дано вершини піраміди А(1,-2,2), В(2,-3,-6), С(5,1,4) і 14. Скласти рівняння площини, яка проходить через точки Відповіді: 1. 4. у-7=0. 5. 8. 96. 9. 1) 243; 2) 6; 3) 121,5. 10. 8. 11. 12. 60°. 13. 4. 14.
Пряма в просторі 3.15. Канонічне та параметричне рівняння прямої в просторі
Аналогічна задача вже розв’язувалась для прямої на площині. Отже, необхідно скласти рівняння прямої Нехай,
– канонічні рівняння прямої. Прирівнюючи кожний з дробів (25) до параметра
Приклад. За точкою М(1,5,2) і напрямним вектором Розв’язання. 1) За формулою (25) запишемо канонічне рівняння прямої
2) Розглянемо два способи побудови прямої Перший спосіб. В системі координат XYZ будуємо вектор Другий спосіб. За формулою (26) записуємо рівняння прямої
Задачі.
1. На прямій Відповідь: 2. Точка Відповідь: Вказівка. Скористатись методикою відповідних задач, розв’язаних в 3.7.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.95.229 (0.009 с.) |

 ,
,  і
і  , що не лежать на одній лінії. Довільна точка
, що не лежать на одній лінії. Довільна точка  відмінна від
відмінна від  , буде знаходитись в площині точок
, буде знаходитись в площині точок 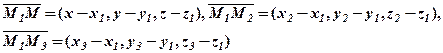
 .
.
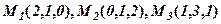 .
.
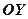 (рис.19).
(рис.19).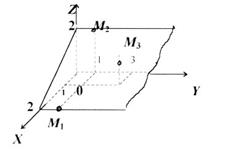


 ,
,  – нормальні вектори площин
– нормальні вектори площин  ,
, 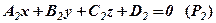 .
. , то
, то 

 , то отримуємо
, то отримуємо (23)
(23) від точки
від точки  до площини
до площини  :
: 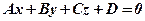 , виражається формулою:
, виражається формулою:


 ,
, . Оскільки
. Оскільки
 а
а  , то формула (21), таким чином, доведена.
, то формула (21), таким чином, доведена. Скласти рівняння площини
Скласти рівняння площини  та знайти висоту
та знайти висоту  піраміди
піраміди 

 2)
2)  3)
3) 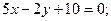 4)
4) 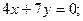 5)
5) 
 у відрізках.
у відрізках. .
. . Необхідно знайти: 1) об’єм піраміди, обмеженої цією площиною та координатними площинами; 2) відстань до цієї площини від початку координат; 3) площу бічної грані, яка відтинається координатними площинами від заданої площини.
. Необхідно знайти: 1) об’єм піраміди, обмеженої цією площиною та координатними площинами; 2) відстань до цієї площини від початку координат; 3) площу бічної грані, яка відтинається координатними площинами від заданої площини. і
і  .
. і
і 
 і
і 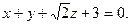
 . Знайти довжину висоти, яка проведена із вершини В.
. Знайти довжину висоти, яка проведена із вершини В. і В(1,-2,8) і перпендикулярна площині
і В(1,-2,8) і перпендикулярна площині 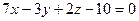 .
.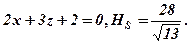 2.
2. 
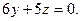 6.
6.  7.
7. 


 , що проходить через дану точку
, що проходить через дану точку 
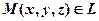 – довільна точка прямої, тоді вектори
– довільна точка прямої, тоді вектори  і
і  колінеарні, а це значить, що координати їх пропорційні, тому отримуємо
колінеарні, а це значить, що координати їх пропорційні, тому отримуємо
 , запишемо параметричні рівняння прямої
, запишемо параметричні рівняння прямої
 необхідно: 1) скласти канонічне рівняння прямої
необхідно: 1) скласти канонічне рівняння прямої  ; 2) побудувати цю пряму.
; 2) побудувати цю пряму.
 і точку М(1,5,2) і проводимо через точку М пряму паралельну вектору
і точку М(1,5,2) і проводимо через точку М пряму паралельну вектору 

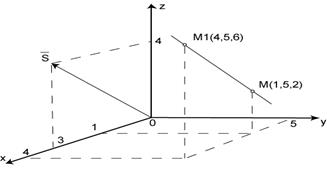 При довільних значеннях t із системи знаходимо координати відповідних точок, які належать прямій
При довільних значеннях t із системи знаходимо координати відповідних точок, які належать прямій  знайти точки, які знаходяться на відстані 10 одиниць від точки
знайти точки, які знаходяться на відстані 10 одиниць від точки  .
. .
. рухається рівномірно з величиною швидкості
рухається рівномірно з величиною швидкості  м/с в напрямку вектора
м/с в напрямку вектора  від початкової точки
від початкової точки  . Знайти координати точки
. Знайти координати точки  с від початку руху.
с від початку руху. .
.


