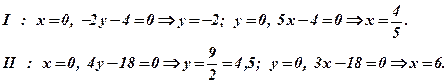Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні задачі на пряму лініюСодержание книги Поиск на нашем сайте
а) Рівняння прямої за двома точками
Приклад. Записати рівняння прямої, якщо б) Відстань від точки
Дійсно, з рис. 8 зрозуміло, що
Рис. 8. де Тоді отримуємо (9). Наприклад, відстань від точки
в) Кут між двома прямими
Рис.9
Оскільки
Отже, – формула тангенса кута між двома прямими. Зауваження. З рис.9 видно, що між прямими Приклад. В рівнобедреному прямокутному трикутнику АВС відома вершина прямого кута С(-1,2) і рівняння гіпотенузи АВ Розв’язання. Рівняння прямої, що проходить через точку С знаходимо за формулою пучка прямих
За умовою ÐА=ÐВ=45°, tg45°=1, тому
Спочатку знайдемо Оскільки поворот прямої АВ на кут 45° проти годинникової стрілки відносно точки А приводить до суміщення з прямою АС, то у формулі (11)
За формулою пучка рівняння прямої АС запишеться
(АС) Аналогічно знайдемо
(ВС) Якщо
– умова паралельності двох прямих. Якщо ж
- умова перпендикулярності двох прямих. Якщо ж прямі задані загальними рівняннями
то кут між ними можна знаходити, як кут між їх нормальними екторами
Рис.10
косинус кута між двома прямими Якщо
– умова паралельності. Якщо ж
– умова перпендикулярності прямих. г) Рівняння прямої, що проходить через задану точку
Розв’язання. Кожного разу, коли задається точка, то рівняння прямої краще знаходити за формулою (5) пучка прямих
де Наприклад, скласти рівняння прямої, що проходить через точку Розв’язання. Із загального рівняння прямої д) Рівняння прямої, що проходить через точку Із загального рівняння
Приклад. Скласти рівняння прямої, що проходить через точку Розв’язання. Із
Відповідь:
е) Точка перетину прямих
Приклад. Знайти точку перетину прямих. Зробити рисунок, побудувавши графіки.
Розв’язання. Розв’яжемо дану систему рівнянь, домноживши перше рівняння на 2 і додавши результат з другим рівнянням
Підставивши
Отже, точка перетину Побудуємо графіки за рівняннями, що входять в систему. Побудову краще виконати у відрізках на осях
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 418; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.188.121 (0.008 с.) |

 і
і 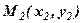 знаходимо з канонічного рівняння (7) оскільки напрямний вектор
знаходимо з канонічного рівняння (7) оскільки напрямний вектор  , то
, то
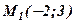 ,
,  . Відповідь:
. Відповідь: 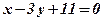 .
. до прямої
до прямої  знаходиться за формулою
знаходиться за формулою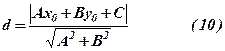
 ,
,
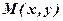 – довільна точка прямої. Вектор
– довільна точка прямої. Вектор  .
.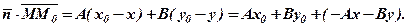 Але із загального рівняння прямої
Але із загального рівняння прямої 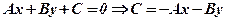 , тому
, тому  а
а 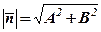 . Отже,
. Отже,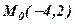 до прямої
до прямої 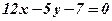 за формулою (9) дорівнює
за формулою (9) дорівнює
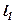 і
і  спочатку знайдемо, коли їх рівняння мають вигляд (див. рис.9)
спочатку знайдемо, коли їх рівняння мають вигляд (див. рис.9)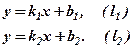
 а
а 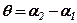 , то
, то

 і
і  - два кути: один – гострий
- два кути: один – гострий  , другий – тупий
, другий – тупий  . Згідно формули (11)
. Згідно формули (11) 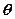 - це той кут між прямими
- це той кут між прямими 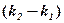 , записана зверху.
, записана зверху. . Скласти рівняння катетів.
. Скласти рівняння катетів. , де кутовий коефіцієнт
, де кутовий коефіцієнт  для прямої АС і
для прямої АС і 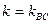 для прямої ВС.
для прямої ВС.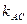 і
і 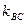 знаходимо за формулою (11), ураховуючи зауваження до неї.
знаходимо за формулою (11), ураховуючи зауваження до неї.
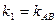 , а
, а 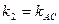 . Із рівняння АВ:
. Із рівняння АВ: 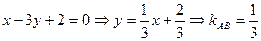 , тому
, тому 
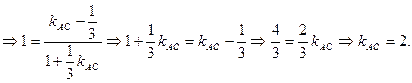

 .
. , а
, а 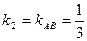 , ÐВ=45°
, ÐВ=45°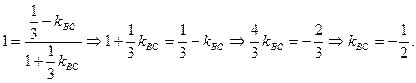 Рівняння прямої ВС:
Рівняння прямої ВС:

 – прямі паралельні, то
– прямі паралельні, то 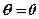 і тоді
і тоді
 , то
, то 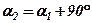 , а
, а або
або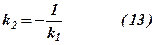

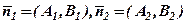 (див. рис. 10);
(див. рис. 10); 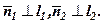



 , то
, то
 ,
, – знаходимо із загального рівняння заданої прямої і умови паралельності прямих (12).
– знаходимо із загального рівняння заданої прямої і умови паралельності прямих (12). паралельно прямій
паралельно прямій 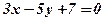 .
. , а за умовою паралельності прямих
, а за умовою паралельності прямих 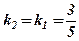 , тоді отримуємо
, тоді отримуємо 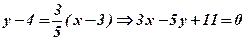 .
.
 , а за умовою перпендикулярності маємо
, а за умовою перпендикулярності маємо  , тоді шукане рівняння за формулою пучка
, тоді шукане рівняння за формулою пучка
 перпендикулярно до прямої
перпендикулярно до прямої  .
. . Тоді
. Тоді
 .
.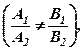 знаходиться як розв’язок системи
знаходиться як розв’язок системи


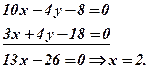
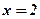 в перше рівняння маємо:
в перше рівняння маємо:
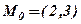 .
.