
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівняння прямої за точкою та нормальнимСтр 1 из 5Следующая ⇒
ІІІ. Аналітична геометрія 3.1. Аналітична геометрія це розділ математики, в якому геометричні задачі розв’язуються алгебраїчним шляхом за допомогою методу координат. В аналітичній геометрії геометричні місця точок або лінії задаються рівняннями, що зв’язують в даній системі координат змінні Означення. Рівнянням лінії в аналітичній геометрії називається співвідношення, (або залежність між змінними Наприклад. 1. Координати точки 2. Точка Пряма лінія на площині Рівняння прямої за точкою та нормальним Вектором Нехай в системі координат Очевидно існує єдина пряма
Рис.1
Доведемо, що лінійне рівняння
є рівнянням прямої Для доведення зауважимо, що скалярний добуток векторів
Далі використаємо очевидну властивість прямої Рівняння (1) називається рівнянням прямої, що проходитьчерез дану точку Приклад. Дана точка М(4,1) і вектор 1) скласти рівняння прямої
2) перевірити, які з точок М1(0,3), М2(-6,6), М3(3;2,5), М4(8,-1) лежать на прямій 3) побудувати пряму Відповіді: 1) (х-4)+2(у-1)=0; 2)
Загальне рівняння прямої
Перетворимо рівняння (1)
Позначивши
— загальне рівняння прямої. Таким чином, прямій лінії Дійсно, нехай пара чисел
Віднімаючи останнє від (3), одержимо співвідношення Приклади
1.Скласти загальне рівняння прямої, що проходить через точку Відповідь:
2.Задані точки Відповідь: Рівняння прямої у відрізках
Побудуємо пряму за загальним рівнянням Покладемо При (див. рис. 2).
Рис.2 Від загального можна перейти до рівняння, в яке будуть входити числа
або, згідно з позначенням, отримуємо рівняння,
яке називається рівнянням прямої у відрізках. Числа Приклади. 1. Записавши рівняння у відрізках, побудувати прямі а) б) в) 2. Знайти площу трикутника, обмеженого прямою
Відповіді: 1. а)
Приклади.
Побудувати лінії: а) б) в) г)
Приклад
1. Перейти до рівняння з кутовим коефіцієнтом а) б)
Відповіді: 1. а)
2. а) 3. г) Приклади
1. На прямій лінії заданої рівнянням Розв’язання. Нехай
Тоді відстань
Відповідь:
2. Точка Розв’язання. Спочатку знайти одиничний вектор
Тоді вектор швидкості
Канонічне рівняння прямої тепер запишется
Після чого скористатись параметричним рівнянням прямої при
Площина Приклад Дано точки М(-4,6,-6) і N(-9,2,-5). Скласти рівняння площини, яка проходить через точку М і перпендикулярна до вектора Розв’язання. За умовою вектор
Підставляючи в рівняння (17) А=-5, В=-4, С=1, а також х1=-4, у1=6, z=-6, маємо Приклади. 1.Побудувати площину Розв’язання. Покладемо
 . (Рис.13) . (Рис.13)
Рис. 13. Рівняння слідів:
2. Знайти об’єм піраміди обмеженої площиною Відповідь: 3.Знайти площу трикутника, який відтиняється координатними площинами від площини Відповідь: Пряма в просторі 3.15. Канонічне та параметричне рівняння прямої в просторі
Аналогічна задача вже розв’язувалась для прямої на площині. Отже, необхідно скласти рівняння прямої Нехай,
– канонічні рівняння прямої. Прирівнюючи кожний з дробів (25) до параметра
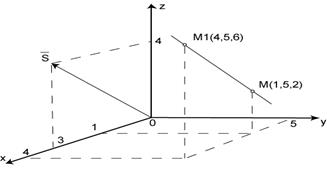
Приклад. За точкою М(1,5,2) і напрямним вектором Розв’язання. 1) За формулою (25) запишемо канонічне рівняння прямої
2) Розглянемо два способи побудови прямої Перший спосіб. В системі координат XYZ будуємо вектор Другий спосіб. За формулою (26) записуємо рівняння прямої
Задачі.
1. На прямій Відповідь: 2. Точка
Відповідь: Вказівка. Скористатись методикою відповідних задач, розв’язаних в 3.7. Пряма лінія і площина Кут між прямою і площиною
Нехай пряма
Кутом між прямою Позначимо через
Рис. 23.
– умова паралельності прямої і площини. І якщо
– умова перпендикулярності прямої і площини. Приклади 1. Знайти кут між прямою Розв’язання. Відповідно до формули (31) з першого рівняння знаходимо напрямний вектор
2. Скласти рівняння площини, яка проходить через точку А(-3,4,-7) і перпендикулярна прямій Розв’язання. Відповідно умові (33) перпендикулярності прямої і площини
Приклади 1.Знайти точку перетину прямої Розв’язання. Запишемо рівняння прямої в параметричному вигляді:
2. Знайти точку N симетричну з точкою М(-1,4,2) відносно площини Розв’язання. Спочатку складемо рівняння прямої, яка проходить через точку М(-1,4,2) перпендикулярно до площини. За напрямний вектор Знайдемо точку перетину знайденої прямої з площиною. З рівняння прямої виражаємо
Отже, симетричною з точкою М(-1,4,2) відносно заданої площини є точка N(5,6,4).
Криві другого порядку
Рівняння вигляду
де хоча б один з коефіцієнтів Рівняння (35) завжди описує пряму лінію. Алгебраїчним рівнянням другого порядку називається всяке рівняння вигляду
де хоча б один з коефіцієнтів Лінії, координати точок яких задовольняють рівняння (36) називаються лініями другого порядку. До ліній другого порядку відносяться: еліпс (зокрема коло), гіпербола, парабола. Вони описуються рівнянням вигляду (36). Однак не кожне рівняння другого порядку завжди описує одну із згаданих ліній. Може, наприклад, вийти так, що рівняння вигляду (36) описує пару прямих ліній або не визначає жодного реального об’єкту.
Приклади. 1. Рівняння 2. Рівняння 3. Рівняння 4. Рівняння 5. Рівняння 6. Рівняння 7. Рівняння Додамо ще, що при відповідному виборі декартової системи координат рівняння (36) для кривих другого порядку набувають простий, так званий канонічний вигляд. Далі розглянемо коротко кожну із кривих другого порядку.
Коло
Означення. Колом називається множина точок Нехай
– рівняння кола радіуса Якщо ж центр кола збігається з початком координат,
-канонічне рівняння кола. Розкриємо дужки в (37) і зведемо його до вигляду (36)
Отже загальне рівняння (36) може описувати коло, якщо
Приклад. Знайти центр кола і радіус, якщо 1. Розв’язання. Згрупуємо відносно
Отже, центр кола в точці
2. Розв’язання.
Сумма квадратів в лівій частині рівності не може бути від’ємною. Дане рівняння не описує кола. Еліпс Означення. Еліпсом називається множина точок площини, сума відстаней яких від двох заданих точок, що називаються фокусами, є величина стала і дорівнює Позначимо фокуси Нехай M ( x, y ) – довільна точка еліпса. Позначимо через r 2 і r 1 – відстані від точки M до фокусів. Згідно з означенням еліпса.
Рис. 24.
Підставимо в (38)
(підносимо до квадрата обидві частини)
Позначимо:
Відмітимо, що за відомою властивістю трикутника (сума двох сторін більша третьої) із
Для побудови еліпса зауважимо, що якщо точка
Точки З (39) знаходимо Якщо Величина відношення міжфокусної відстані до великої осі називається ексцентриситетом еліпса і, після скорочення на 2, позначається
Рис. 25.
Еліпс можна побудувати механічним способом. Із канонічного рівняння знаходимо півосі Задача 1. Задано еліпс рівнянням 1) переконатись, що точки М0 і М1 лежать на еліпсі; 2) знайти півосі еліпса та координати його фокусів; 3) побудувати еліпс і точки М0 і М1; 4) знайти відстань від точки М0 до фокусів; 5) упевнитись, що сума цих відстаней дорівнює довжині великої осі; 6) знайти ексцентриситет еліпса. Розв’язання. 1) Підставимо координати x=4; y=1,8 точки М0 в ліву частину рівняння еліпса:
2) З канонічного 3) Відкладемо значення півосі 4) Знайдемо фокальні радіуси точки М0 5) Знайдемо суму 6) Ексцентриситет знаходиться за формулою Задача 2. Знайти осі, вершини і фокуси еліпса Розв’язання. Зведемо дане рівняння до канонічного вигляду (див. рівняння (39)), перенесемо вільний член вправо і почленно розділимо на нього всю рівність
Порівнюючи останнє рівняння з рівнянням (39), маємо Зауваження. Якщо у канонічному рівнянні
| Поделиться:
| |
 і
і  , які називаються ще поточними координатами. Якщо в елементарній геометрії лінії та їх властивості вивчались в основному за допомогою геометричних побудов, то в аналітичній геометрії вони вивчаються шляхом дослідження рівнянь цих ліній.
, які називаються ще поточними координатами. Якщо в елементарній геометрії лінії та їх властивості вивчались в основному за допомогою геометричних побудов, то в аналітичній геометрії вони вивчаються шляхом дослідження рівнянь цих ліній. , яке задовольняють координати довільної точки
, яке задовольняють координати довільної точки 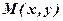 цієї лінії, а якщо точка
цієї лінії, а якщо точка  не лежить на цій лінії, то її координати не задовольняють дане рівняння.
не лежить на цій лінії, то її координати не задовольняють дане рівняння. задовольняють рівняння прямої
задовольняють рівняння прямої 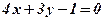 , отже, ця точка лежить на прямій. Координати точки
, отже, ця точка лежить на прямій. Координати точки  дане рівняння не задовольняють:
дане рівняння не задовольняють: 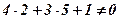 . Отже,
. Отже,  лежить на колі
лежить на колі  , оскільки
, оскільки  , а точка
, а точка  не лежить на цьому колі, бо
не лежить на цьому колі, бо  .
. задана точка
задана точка  і ненульовий вектор
і ненульовий вектор  (рис.1).
(рис.1). , що проходить через точку
, що проходить через точку  перпендикулярно напрямкові вектора
перпендикулярно напрямкові вектора  (в цьому випадку
(в цьому випадку 

 в координатній формі збігається з лівою частиною рівняння (1).
в координатній формі збігається з лівою частиною рівняння (1).
 перпендикулярні, тоді і тільки тоді, коли точка
перпендикулярні, тоді і тільки тоді, коли точка  лежить на
лежить на  для всіх точок
для всіх точок  Необхідно:
Необхідно: , що проходить через точку М перпендикулярно вектору
, що проходить через точку М перпендикулярно вектору 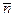 ;
; ,
, 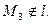
 .
.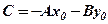 , отримаємо
, отримаємо
 і
і  відмінний від нуля, можна побудувати пряму.
відмінний від нуля, можна побудувати пряму. задовольняє рівняння (3), тобто
задовольняє рівняння (3), тобто .
. , яке визначає пряму за вектором
, яке визначає пряму за вектором 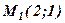 перпендикулярно вектору
перпендикулярно вектору  .
. .
.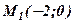 і
і  . Скласти загальне рівняння прямої, що проходить через точку
. Скласти загальне рівняння прямої, що проходить через точку  .
. .
. за умови, що
за умови, що  – відмінні від нуля. Для цього досить знайти дві точки, що належать цій прямій. Такі точки іноді зручніше знаходити на координатних осях.
– відмінні від нуля. Для цього досить знайти дві точки, що належать цій прямій. Такі точки іноді зручніше знаходити на координатних осях. , тоді
, тоді  .
.
 . Позначимо
. Позначимо  . Знайдені точки
. Знайдені точки  і
і  відкладемо на осях OX i OY і через них проводимо пряму
відкладемо на осях OX i OY і через них проводимо пряму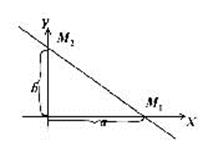
 і
і  :
:
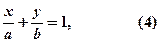
 ;
; ;
; .
. та координатними осями.
та координатними осями. . Записати рівняння інших сторін.
. Записати рівняння інших сторін. ; б)
; б)  ; в)
; в)  . 2. 7,5. 3.
. 2. 7,5. 3.  ;
;  ;
;  . 4.
. 4.  .
.



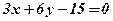 ;
; .
. ; б)
; б)  .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. : а)
: а) 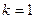 ; б)
; б)  ; в)
; в)  ;
;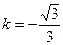 . 4.
. 4.  ;
;  .
. , знайти точку M(x,y), що знаходяться від точки
, знайти точку M(x,y), що знаходяться від точки  цієї прямої на відстані 10 одиниць.
цієї прямої на відстані 10 одиниць. запишемо
запишемо  . За умовою
. За умовою 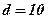 . Оскільки точка
. Оскільки точка  належить прямій
належить прямій 

 . За умовою
. За умовою  , або
, або  . З параметричного рівняння
. З параметричного рівняння

 в напрямку вектора
в напрямку вектора  від початкової точки
від початкової точки 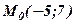 . Знайти координати точки
. Знайти координати точки  с від початку руху.
с від початку руху. . Його координати це напрямні косинуси
. Його координати це напрямні косинуси .
.
 параметричне рівняння.
параметричне рівняння. . Відповідь:
. Відповідь:  .
. .
.
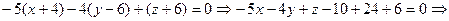
 .
.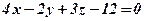 і записати її рівняння у відрізках, а також рівняння слідів на відповідних координатних площинах.
і записати її рівняння у відрізках, а також рівняння слідів на відповідних координатних площинах. , тоді
, тоді 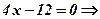
 . Аналогічно при
. Аналогічно при  знаходимо
знаходимо 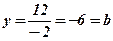 , при
, при  , тоді рівняння у відрізках запишеться
, тоді рівняння у відрізках запишеться
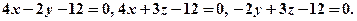
 .
. .
.  , що проходить через дану точку
, що проходить через дану точку  паралельно напрямному вектору
паралельно напрямному вектору 
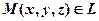 – довільна точка прямої, тоді вектори
– довільна точка прямої, тоді вектори  і
і  колінеарні, а це значить, що координати їх пропорційні, тому отримуємо
колінеарні, а це значить, що координати їх пропорційні, тому отримуємо
 , запишемо параметричні рівняння прямої
, запишемо параметричні рівняння прямої
 необхідно: 1) скласти канонічне рівняння прямої
необхідно: 1) скласти канонічне рівняння прямої 
 і точку М(1,5,2) і проводимо через точку М пряму паралельну вектору
і точку М(1,5,2) і проводимо через точку М пряму паралельну вектору 

 При довільних значеннях t із системи знаходимо координати відповідних точок, які належать прямій
При довільних значеннях t із системи знаходимо координати відповідних точок, які належать прямій  знайти точки, які знаходяться на відстані 10 одиниць від точки
знайти точки, які знаходяться на відстані 10 одиниць від точки  .
. .
. рухається рівномірно з величиною швидкості
рухається рівномірно з величиною швидкості  м/с в напрямку вектора
м/с в напрямку вектора  від початкової точки
від початкової точки  . Знайти координати точки
. Знайти координати точки  с від початку руху.
с від початку руху. .
. задані відповідно своїми рівняннями
задані відповідно своїми рівняннями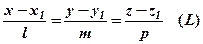 і
і 
 величину цього кута. Кут між нормальним вектором
величину цього кута. Кут між нормальним вектором  і напрямним вектором
і напрямним вектором  дорівнює кутові
дорівнює кутові  , тому
, тому 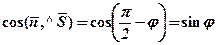 . Отже,
. Отже,
 З рис. 23 видно, що
З рис. 23 видно, що 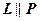 , коли
, коли 
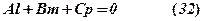
 , то
, то 

 і площиною
і площиною 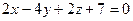 .
. з рівняння площини – нормальний вектор
з рівняння площини – нормальний вектор  тоді
тоді


 за нормальний вектор площини можна взяти паралельний йому напрямний вектор прямої
за нормальний вектор площини можна взяти паралельний йому напрямний вектор прямої  Використовуючи рівняння площини, яка проходить через точку А(-3,4,-7) перпендикулярно вектору
Використовуючи рівняння площини, яка проходить через точку А(-3,4,-7) перпендикулярно вектору  маємо
маємо
 з площиною
з площиною  .
. Підставимо вирази для x, y, z в загальне рівняння площини
Підставимо вирази для x, y, z в загальне рівняння площини Звідки
Звідки 

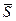 можна взяти нормальний вектор
можна взяти нормальний вектор  даної площини (див. умову (33) попереднього параграфа
даної площини (див. умову (33) попереднього параграфа 
 і підставляємо у рівняння площини
і підставляємо у рівняння площини
 – точка перетину прямої і площини. Ця точка є серединою між двома симетричними відносно площини точками М(-1,4,2) і N(XN, YN, ZN), тобто
– точка перетину прямої і площини. Ця точка є серединою між двома симетричними відносно площини точками М(-1,4,2) і N(XN, YN, ZN), тобто

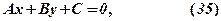
 відмінний від нуля, називається алгебраїчним рівнянням першого порядку, або першого степеня відносно змінних
відмінний від нуля, називається алгебраїчним рівнянням першого порядку, або першого степеня відносно змінних  .
.
 .
. описує коло.
описує коло. описує параболу.
описує параболу.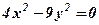 розпадається на дві прямі
розпадається на дві прямі  і
і  , що перетинаються.
, що перетинаються. , тобто
, тобто  розпадаються на дві паралельні прямі
розпадаються на дві паралельні прямі 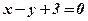 і
і 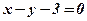 .
. , тобто
, тобто 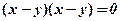 розпадається на дві прямі, що збігаються.
розпадається на дві прямі, що збігаються. має своїм розв’язком тільки одну точку
має своїм розв’язком тільки одну точку  .
. не описує в області дійсних чисел ніякого геометричного місця точок.
не описує в області дійсних чисел ніякого геометричного місця точок. .
. – центр кола,
– центр кола,  – довільна точка кола. За умовою
– довільна точка кола. За умовою  , а за формулою відстані між двома точками маємо
, а за формулою відстані між двома точками маємо
 з центром в точці
з центром в точці  , то отримуємо
, то отримуємо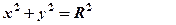
 .
. а
а 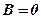 . За цих умов, щоб знайти центр кола і його радіус, потрібно виділити повний квадрат.
. За цих умов, щоб знайти центр кола і його радіус, потрібно виділити повний квадрат.

 , а радіус
, а радіус  . Пропонуємо побудувати це коло.
. Пропонуємо побудувати це коло.

 .
. і
і  . Припустимо, що відстань
. Припустимо, що відстань  – фокусна відстань. Щоб отримати канонічне рівняння еліпса розмістимо
– фокусна відстань. Щоб отримати канонічне рівняння еліпса розмістимо 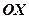 , симетрично щодо початку координат. Тоді фокуси матимуть координати
, симетрично щодо початку координат. Тоді фокуси матимуть координати  і
і  (див. рис. 24).
(див. рис. 24). . (38)
. (38)
 ,
,  і звільнимось від ірраціональності, піднісши обидві частини до квадрата, отримаємо:
і звільнимось від ірраціональності, піднісши обидві частини до квадрата, отримаємо:


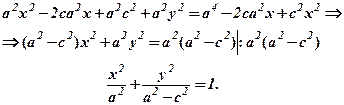
 , отримаємо канонічне рівняння еліпса:
, отримаємо канонічне рівняння еліпса:
 маємо
маємо 
 Оскільки
Оскільки  , а тому
, а тому (*)
(*) належить еліпсу, тобто задовольняє рівняння (39), то точки
належить еліпсу, тобто задовольняє рівняння (39), то точки  теж задовольняють це рівняння: із
теж задовольняють це рівняння: із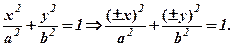
 – розміщені симетрично відносно осей координат. Отже, еліпс – фігура симетрична відносно координатних осей. Тому досить побудувати графік в першій чверті, а тоді симетрично продовжити його.
– розміщені симетрично відносно осей координат. Отже, еліпс – фігура симетрична відносно координатних осей. Тому досить побудувати графік в першій чверті, а тоді симетрично продовжити його. , для І -ої чверті
, для І -ої чверті 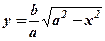 .
. , то
, то  . Якщо ж
. Якщо ж  , то
, то 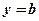 . Точки
. Точки  і
і  , а також симетричні з ними
, а також симетричні з ними 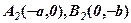 – вершини еліпса, точка
– вершини еліпса, точка 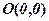 – центр еліпса,
– центр еліпса,  – велика вісь,
– велика вісь,  – мала вісь еліпса. Якщо
– мала вісь еліпса. Якщо  І чверті, то із
І чверті, то із  . Значення ексцентриситета характеризує ступінь “сплющенності” еліпса. Якщо
. Значення ексцентриситета характеризує ступінь “сплющенності” еліпса. Якщо  , то
, то  – маємо коло. Якщо ж
– маємо коло. Якщо ж  , то
, то 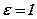 – еліпс вироджується у відрізок. В невироджених випадках
– еліпс вироджується у відрізок. В невироджених випадках  Для фокальних радіусів наведемо без доведення такі формули:
Для фокальних радіусів наведемо без доведення такі формули: (**)
(**)
 – півфокусну відстань. Будуємо фокуси
– півфокусну відстань. Будуємо фокуси  закріпляємо в точках
закріпляємо в точках  і точки М0(4;1,8), М1(3;2,4). Необхідно:
і точки М0(4;1,8), М1(3;2,4). Необхідно: – точка М0 лежить на еліпсі. Аналогічно для М1(3;2,4):
– точка М0 лежить на еліпсі. Аналогічно для М1(3;2,4): – точка М1 лежить на еліпсі.
– точка М1 лежить на еліпсі. і даного рівняння
і даного рівняння  еліпса випливає
еліпса випливає  З рівності (*) цього параграфа
З рівності (*) цього параграфа 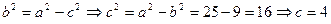 – півфокусна відстань. Координати фокусів F1(4;0) і F2(-4;0).
– півфокусна відстань. Координати фокусів F1(4;0) і F2(-4;0). симетрично відносно точки О(0,0) на осі ОХ. Аналогічно b=3 відкладемо на осі ОУ.
симетрично відносно точки О(0,0) на осі ОХ. Аналогічно b=3 відкладемо на осі ОУ.

 , що відповідає означенню еліпса.
, що відповідає означенню еліпса.
 . Побудувати еліпс.
. Побудувати еліпс.
 Звідси знаходимо осі еліпса 2а=24, 2b=10 і координати вершин А1(12,0), А2(-12,0), В1(0,5), В2(0,-5). Далі із формули
Звідси знаходимо осі еліпса 2а=24, 2b=10 і координати вершин А1(12,0), А2(-12,0), В1(0,5), В2(0,-5). Далі із формули  . Отже, фокусами еліпса є точки F1(
. Отже, фокусами еліпса є точки F1( ,0) і F2(
,0) і F2( ,0). Для побудови еліпса відкладаємо на осях ОХ і ОУ вершини А1, В1, А2, В2 відповідно і з’єднуємо їх плавною лінією (див. попередню задачу).
,0). Для побудови еліпса відкладаємо на осях ОХ і ОУ вершини А1, В1, А2, В2 відповідно і з’єднуємо їх плавною лінією (див. попередню задачу).


