
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение дуги окружности в комплексной форме.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
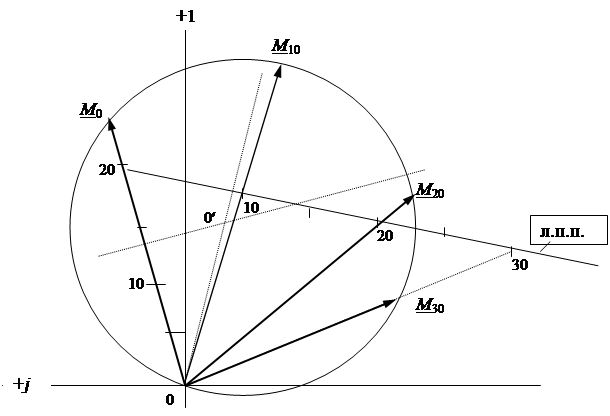
При изменении параметров одного из элементов сложной цепи токи всех ветвей, напряжения на всех элементах изменяются так, что концы векторов этих величин описывают дуги некоторых окружностей. Для исследования зависимости любой векторной величины (U, I) от переменного параметра достаточно определить дугу окружности, по которой перемещается конец этого вектора, другими словами, построить круговую диаграмму. Уравнение дуги окружности в комплексной форме имеют вид:
где М = Мejb – исследуемый вектор, M 0 - вектор-хорда дуги окружности, a = const – постоянный коэффициент, y = const – постоянный угол, n = var = (0 - ¥) – переменный параметр. Порядок построения круговой диаграммы по заданному уравнению:
1) На комплексной плоскости в выбранном масштабе mм откладывают вектор М 0=5ej20 - хорду дуги окружности (рис. 80). 2) Вдоль вектора-хорды М 0 от его начала в выбранном масштабе mа откладывают отрезок, равный коэффициенту “ а ”. 3) Из конца отрезка “ а ” под углом - y к вектору М 0 проводят линию переменного параметра (л.п.п.), на которой наносят масштаб mа, принятый ранее для отрезка “ а ”. 4) Определят положение центра дуги как точку пересечения двух перпендикуляров: первый проводят через середину вектора-хорды М 0, а второй – из начала координат к линии переменного параметра. 5) Проводят рабочую дугу по ту сторону от вектора-хорды М 0, где расположена линия переменного параметра. 6) Вдоль линии переменного параметра откладывают текущее значение параметра “ n ” соединяют точку с началом вектора М 0 (началом координат) и продолжают прямую линию до пересечения с дугой окружности. Искомый вектор М соответствует отрезку от начала координат до точки пересечения прямой линии с дугой окружности, при этом модуль вектора равен длине отрезка в масштабе mм, а начальная фаза вектора – углу между вещественной осью +1 и напрвлением вектора. На рис. 80 показано семейство векторов М, построенных для различных значений переменного параметра “ n ” (n = 0; 10; 20; 30). 2. Круговая диаграмма тока и напряжений для элементов последовательной цепи
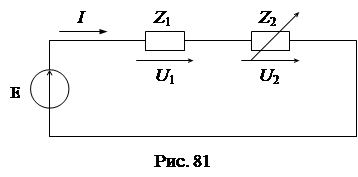
Рассмотрим схему цепи, состоящую из последовательно включенных источника ЭДС E и пассивных элементов Z 1,и Z 2 (рис. 81). Задано, что E = Eeja =const, Z 1 = Z 1 ejj 1 = const, Z 2 = Z 2 ejj 2, где j 2=const, a Z 2 = var= 0÷¥ - переменный параметр.
Преобразуем уравнение закона Ома для схемы к виду дуги окружности в комплексной форме:
где М 0 = I к= E / Z 1 – ток короткого замыкания, соответствует вектору-хорде дуги окружности, Z 2 = n = var – переменный параметр, Z 1= a = const- постоянный коэффициент, j 2 - j 1= y = const – постоянный угол. Таким образом, уравнение для тока I является уравнением дуги окружности.
Напряжение на первом элементе представляет собой уравнение дуги окружности:
Напряжение на втором элементе представляет собой уравнение дуги окружности:
Для каждого из векторов I, U 1, U 2 может быть построена круговая диаграмма согласно полученным уравнениям и по ним исследована их зависимость от переменного параметра n = Z 2.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 467; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.69.138 (0.008 с.) |


 ,
,

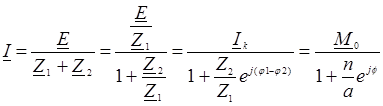 ,
,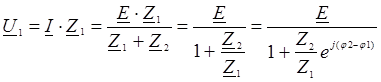 .
.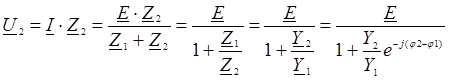 .
.


