
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При несимметричном напряженииСодержание книги
Поиск на нашем сайте
Пусть к симметричному трехфазному приемнику, например электродвигателю, приложена несимметричная система напряжений
Разложим несимметричную систему напряжений U A, U B, U C на симметричные составляющие прямой, обратной и нулевой последовательностей:
Применим к расчету схемы метод наложения и выполним расчет токов отдельно для каждой симметричной составляющей напряжения. Так как для каждой из симметричных составляющих трехфазная схема генератор-приемник полностью симметрична, то расчет режима можно выполнять только для одной фазы А, соответственно трехфазную схему следует заменить тремя однофазными отдельно для каждой составляющей (рис. 109а, б, в). В симметричном режиме для прямой и обратной последовательностей ток в нулевом проводе равен нулю и, следовательно, напряжение U A 0 = I A 0 Z 0 + I N× Z N = I A 0(Z 0 + 3 Z N) Согласно полученному уравнению схема замещения для нулевой последовательности получит вид (рис. 109в), в которой последовательно с сопротивлением фазы Z 0 включается утроенное сопротивление нейтрали 3 Z N. В схемах для отдельных симметричных составляющих (рис. 4а, б, в) обозначены Z 1, Z 2, Z 0 - комплексные сопротивления фазы приемника для токов соответственно прямой, обратной и нулевой последовательностей. Для приемников с вращающимся магнитным полем эти сопротивления существенно отличаются.
По закону Ома в каждой из схем рис. 109а, б, в производится расчет токов прямой, обратной и нулевой последовательностей:
Действительные токи в исходной схеме (рис. 108) определяются по методу наложения, как векторные суммы токов прямой, обратной и нулевой последовательностей: I A = I A 1 + I A 2 + I A 0,
I B = I B 1 + I B 2 + I B 0 = a 2× I A 1 + a × I A 2 + I A 0, I C = I C 1 + I C 2 + I C 0 = a × I A 1 + a 2× I A 2 + I A 0.
Комплексные сопротивления фаз статичных трехфазных приемников (осветительная нагрузка, нагревательные приборы и др.) не зависят от вида последовательности, для таких приемников
|
|||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.93.183 (0.009 с.) |

 U A, U B, U C. Для получения общих закономерностей введем в схему нулевой провод с сопротивлением Z N. Схема цепи примет вид (рис. 108):
U A, U B, U C. Для получения общих закономерностей введем в схему нулевой провод с сопротивлением Z N. Схема цепи примет вид (рис. 108):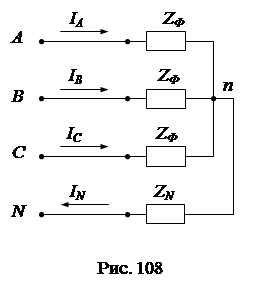

 ,
, ,
, .
. . Это означает, что сопротивление в нейтральном проводе Z N не оказывает влияния на фазные токи и не должно включаться в схемы для этих последовательностей (рис. 109а, б). Токи нулевой последовательности во всех фазах совпадают и могут замкнуться только через нулевой провод: I N = I A 0 + I B 0 + I C 0 = 3 I A 0. По 2-му закону Кирхгофа для нулевой последовательности (рис. 3) получим:
. Это означает, что сопротивление в нейтральном проводе Z N не оказывает влияния на фазные токи и не должно включаться в схемы для этих последовательностей (рис. 109а, б). Токи нулевой последовательности во всех фазах совпадают и могут замкнуться только через нулевой провод: I N = I A 0 + I B 0 + I C 0 = 3 I A 0. По 2-му закону Кирхгофа для нулевой последовательности (рис. 3) получим: 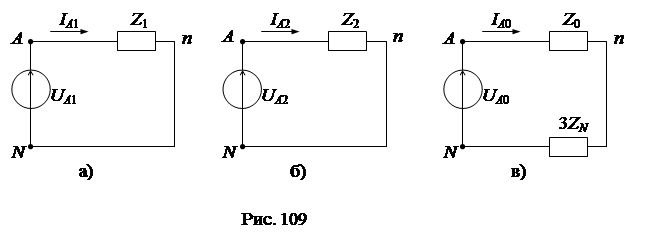
 ;
;  ;
; 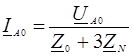 .
.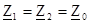 . Расчет токов таких приемников может выполняться обычными методами. Для трехфазных приемников, в которых существует вращающееся магнитное поле (электродвигатели, генераторы), сопротивления фаз для токов разных последовательностей существенно отличаются (
. Расчет токов таких приемников может выполняться обычными методами. Для трехфазных приемников, в которых существует вращающееся магнитное поле (электродвигатели, генераторы), сопротивления фаз для токов разных последовательностей существенно отличаются (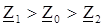 ). Расчет токов таких приемников при несимметричном напряжении должен производиться исключительно методом симметричных составляющих.
). Расчет токов таких приемников при несимметричном напряжении должен производиться исключительно методом симметричных составляющих.


