Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Т.6. Топологические методы расчета электрических цепейСодержание книги
Поиск на нашем сайте
1.Топологические определения схемы
С появлением ЭВМ и их широким применением для решения сложных математических задач были разработаны специальные топологические расчёта сложных электрических цепей, графов и матриц. Схема сложной электрической цепи (рис. 83а) может быть заменена (представлена) направленным графом (рис. 83б) с соблюдением следующих условий: 1)узлы графа соответствуют узлам схемы; 2)ветви графа соответствуют ветвям схемы; 3) направление ветвей соответствует направлению токов в ветвях схемы.
Любая часть графа называется подграфом. Минимальный связанный подграф, соединяющий все узлы графа и не образующий контуров, называется деревом графа (на схеме графа обозначается жирной линией). Для конкретного графа может быть составлено определенное множество вариантов деревьев, но в расчете схемы принимается любой из вариантов. Ветви графа, не входящие в его дерево, называются связями или хордами. Структура графа и соответственно структура электрической схемы может быть описана с помощью топологических матриц или матриц соединения. Таких матриц несколько, для расчета электрических цепей используются две основные: В общем случае сложная схема содержит «m» ветвей и «n» узлов, при этом максимальное число ветвей зависит от числа узлов: Составим таблицу соединений «узлы-ветви» руководствуясь следующими правилами: 1 – ветвь выходит из узла, -1 – ветвь входит в узел, 0 – отсутствие связи с узлом.
Т а б л и ц а 1
Так как каждая ветвь имеет только один вход (-1) и один выход (+1), то сумма чисел по вертикали для любого столбца равна нулю. Из этого следует, что независимыми являются только 3 из 4 строк таблицы. Матрица соединений
Т а б л и ц а 2
Размерность матрицы соединений Независимыми называются контуры графа, образованные одной из хорд и ветвями дерева. Число независимых контуров соответствующих числу хорд графа: Составим таблицу соединений «контуры-ветви», руководствуясь следующими правилами: 1 – направление ветви совпадает с направлением обхода контура, -1 – направление ветви не совпадает с направлением обхода контура, 0 - ветвь не входит в контур. Т а б л и ц а 3
Данная таблица получила название матрицы соединений Если матрицы соединений
2. Уравнения Ома и Кирхгофа в матричной форме
Если в исследуемой сложной схеме содержатся параллельно включенные ветви, то для составления матриц соединений такие ветви необходимо заменить (объединить) одной эквивалентной ветвью. В общем случае любая ветвь схемы кроме комплексного сопротивления (проводимости)
Ток ветви I к, напряжение ветви U к = j 1 - j 2. Из потенциального уравнения ветви
Для всех «m» ветвей составим систему уравнений по этой форме:
Заменим полученную систему из «m» уравнений матричной формой. Для этой цели введем следующие обозначения матриц:
Уравнения Ома в матричной форме получат вид:
Уравнения Кирхгофа в обычной форме имеют вид:
Система уравнений Кирхгофа в матричной форме получается через матрицы соединений
Составленная система уравнений содержит “ m ” неизвестных токов и “ m ” неизвестных напряжений, всего 2“ m ” неизвестных, и непосредственно не может быть решена.
 из матричных уравнений закона Ома, получим: из матричных уравнений закона Ома, получим:
Для сравнения приведем те же уравнения в обычной форме:
 из матричного уравнения закона Ома, получим: из матричного уравнения закона Ома, получим:
Для сравнения приведем те же уравнения в обычной форме:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.193.175 (0.01 с.) |


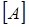 - матрица соединений «узлы-ветви» и
- матрица соединений «узлы-ветви» и  - матрица соединений «контуры-ветви».
- матрица соединений «контуры-ветви».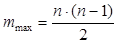 .
. «узлы-ветви» (табл. 2) получается из приведенной выше таблицы путем вычеркивания любой строки (например, строки №4):
«узлы-ветви» (табл. 2) получается из приведенной выше таблицы путем вычеркивания любой строки (например, строки №4): «узлы-ветви» равна
«узлы-ветви» равна 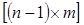 , где n -1 – число независимых узлов, m – число ветвей.
, где n -1 – число независимых узлов, m – число ветвей. , контуры нумеруются по номеру хорды (1, 2, 3). Направление обхода контура принимается по направлению хорды, которая входит в состав этого контура.
, контуры нумеруются по номеру хорды (1, 2, 3). Направление обхода контура принимается по направлению хорды, которая входит в состав этого контура. - «контуры-ветви».Размерность матрицы соединений
- «контуры-ветви».Размерность матрицы соединений  равна
равна  , где
, где  – число независимых контуров, m – число ветвей.
– число независимых контуров, m – число ветвей.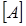 и
и  составлены верно, то должно выполняться условие:
составлены верно, то должно выполняться условие:  .
.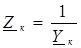 может содержать источник ЭДС Е к, источник тока J к. Схема и граф обобщенной ветви показаны на рис. 1а, б:
может содержать источник ЭДС Е к, источник тока J к. Схема и граф обобщенной ветви показаны на рис. 1а, б: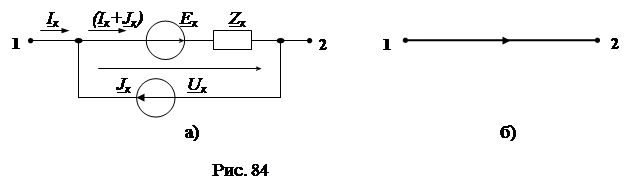
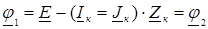 следуют:
следуют: - уравнения Ома для к -ой ветви.
- уравнения Ома для к -ой ветви.


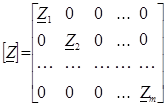 ;
; 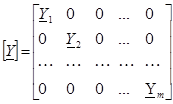
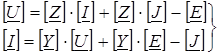
 - первый закон Кирхгофа для узлов,
- первый закон Кирхгофа для узлов,  - второй закон Кирхгофа для контуров.
- второй закон Кирхгофа для контуров. и
и  :
: