
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мощность трехфазной цепи и способы ее измеренияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Активная и реактивная мощности трехфазной цепи, как для любой сложной цепи, равны суммам соответствующих мощностей отдельных фаз:
где IA, UA, IB, UB, IC, UC – фазные значения токов и напряжений. В симметричном режиме мощности отдельных фаз равны, а мощность всей цепи может быть получена путем умножения фазных мощностей на число фаз:
В полученных выражениях заменим фазные величины на линейные. Для схемы звезды верны соотношения
Для схемы треугольника верны соотношения: Uф=Uл; Iф=Iл /
Следовательно, независимо от схемы соединения (звезда или треугольник) для симметричной трехфазной цепи формулы для мощностей имеют одинаковый вид:
В приведенных формулах для мощностей трехфазной цепи подразумеваются линейные значения величин U и I, но индексы при их обозначениях не ставятся. Активная мощность в электрической цепи измеряется прибором, называемым ваттметром, показания которого определяется по формуле:
Для измерения активной мощности всей трехфазной цепи в зависимости от схемы соединения фаз нагрузки и ее характера применяются различные схемы включения измерительных приборов. Для измерения активной мощности симметричной трехфазной цепи применяется схема с одним ваттметром, который включается в одну из фаз и измеряет активную мощность только этой фазы (рис. 99). Активная мощность всей цепи получается путем умножения показания ваттметра на число фаз: Для измерения активной мощности в четырехпроводных трехфазных цепях (при наличии нулевого провода) применяется схема с тремя приборами (рис. 100), в которой производится измерение активной мощности каждой фазы в отдельности, а мощность всей цепи определяется как сумма показаний трех ваттметров:
Для измерения активной мощности в трехпроводных трехфазных цепях (при отсутствии нулевого провода) применяется схема с двумя приборами (рис. 101).
При отсутствии нулевого провода линейные (фазные) ток связаны между собой уравнением 1-го закона Кирхгофа:
Таким образом, сумма показаний двух ваттметров равна активной трехфазной мощности, при этом показание каждого прибора в отдельности зависит не только величины нагрузки но и от ее характера. На рис. 102 показана векторная диаграмма токов и напряжений для симметричной нагрузки. Из диаграммы следует, что показания отдельных ваттметров могут быть определены по формулам:
Анализ полученных выражений позволяет сделать следующие выводы. При активной нагрузке (φ = 0), показания ваттметров равны (W 1 = W 2). При активно-индуктивной нагрузке(0 ≤ φ ≤ 900) показание первого ваттметра меньше, чем второго (W 1 < W 2), а при φ >600 показание первого ваттметра становится отрицательным (W 1<0). При активно-емкостной нагрузке(0 ≥ φ ≥ -900) показание второго ваттметра меньше, чем первого (W 1> W 2), а при φ <-600 показание второго ваттметра становится отрицательным.
8.Вращающееся магнитное поле
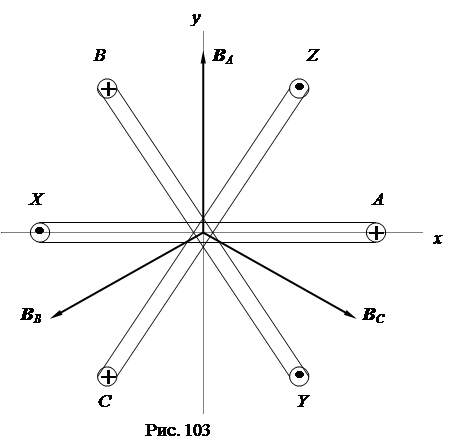
Одним из важнейших достоинств трехфазной системы является возможность получения с ее помощью кругового вращающегося магнитного поля, которое лежит в основе работы трехфазных машин (генераторов и двигателей). Для получения кругового вращающегося магнитного поля необходимо и достаточно выполнить два условия. Условие первое: необходимо 3 p одинаковых катушки (p =1, 2, 3,….) расположить в пространстве так, чтобы их оси были расположены в одной плоскости и сдвинуты взаимно на равные углы ∆ α =360o/3 p. Условие второе: необходимо пропустить по катушкам равные по амплитуде и сдвинутые во времени на ∆ t = T /3 или ∆ ωt = 360o/3=120o переменные токи (симметричный трехфазный ток). При соблюдении указанных условий в пространстве вокруг катушек будет создано круговое вращающееся магнитное поле с постоянной амплитудой индукции Вmax вдоль его оси и с постоянной угловой скоростью вращения ωп. На рис. 103 показано пространственное расположение трех (p = 1) одинаковых катушек под равными углами в 120o согласно первому условию. По катушкам, по направлению от их начал (A, B, C) к концам (X, Y, Z) протекает симметричный трехфазный ток:
iA = Im×sin(wt+ 0 ), iB = Im×sin(wt- 1200 ), iC = Im×sin(wt+ 1200 ). Магнитное поле, создаваемое каждой катушкой в отдельности, пропорционально току катушки (B = k × i), следовательно магнитные поля отдельных катушек в центре координат образуют симметричную трехфазную систему В(t): BA = Bm×sin(wt+ 0 ), BB = Bm×sin(wt- 1200 ), BC = Bm×sin(wt+ 1200 ).
Положительные направления магнитных полей каждой катушки (векторов B A, B B, B C) в пространстве определяются по правилу правоходового винта согласно принятым положительным направлениям токов катушек (рис. 103). Результирующий вектор индукции магнитного поля B для любого момента времени может быть найден путем пространственного сложения векторов B A, B B, B C отдельных катушек. Определим значение результирующего вектора индукции магнитного поля B для нескольких моментов времени ωt = 00; 300; 600. Пространственное сложение векторов
Анализ таблицы показывает, что результирующий вектор индукции магнитного поля
В технике для характеристики вращения магнитного поля пользуются понятием частоты вращения:
С изменением числа p пространственная картина магнитного поля изменяется: при p =1 магнитное поле имеет два полюса (или одну пару полюсов), при p =2 – четыре полюса (или 2 пары полюсов) и т.д. (рис. 105). По этой причине число p = 1, 2, 3,… называют числом пар полюсов магнитного поля.
Частоту вращения магнитного поля можно изменять плавно изменением частоты питающего тока f, и ступенчато - изменением числа пар полюсов p. В промышленных условиях оба способа регулирования частоты вращения поля являются технически и экономически малоэффективными. При постоянной частоте промышленного тока f =50 Гц шкала синхронных частот вращения магнитного поля в функции числа пар полюсов выглядит следующим образом:
Для изменения направления вращения магнитного поля достаточно изменить порядок следования фаз питающего тока или, попросту, поменять местами две любые фазы источника между собой.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 709; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.37.178 (0.01 с.) |

 ,
, ,
,
 ,
, ,
, .
. ;
;  , тогда получим:
, тогда получим: .
.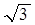 , тогда получим:
, тогда получим:
 [Вт],
[Вт], [вар],
[вар], [ВА].
[ВА]. , где U w, I w - векторы напряжения и тока, подведенные к обмоткам прибора.
, где U w, I w - векторы напряжения и тока, подведенные к обмоткам прибора.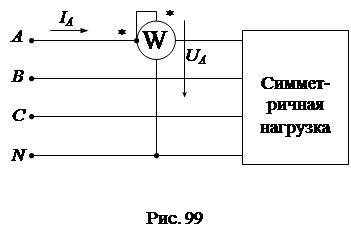
 . Схема с одним ваттметром может быть использована только для ориентированной оценки мощности и неприменима для точных и коммерческих измерений.
. Схема с одним ваттметром может быть использована только для ориентированной оценки мощности и неприменима для точных и коммерческих измерений. .
.

 . Сумма показаний двух ваттметров равна:
. Сумма показаний двух ваттметров равна:

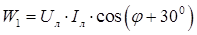 ,
,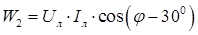 .
.
 выполним графически (рис. 104а, б, в). Результаты расчета сведены в отдельную таблицу:
выполним графически (рис. 104а, б, в). Результаты расчета сведены в отдельную таблицу: /2× Bm
/2× Bm

 имеет постоянную амплитуду (Вmax =3/2× Bm) и равномерно вращается в пространстве в положительную сторону по направлению катушки А к катушке В с угловой скоростью ωп, равной угловой частоте тока ω. В общем случае угловая скорость вращения магнитного поля зависит еще и от числа катушек:
имеет постоянную амплитуду (Вmax =3/2× Bm) и равномерно вращается в пространстве в положительную сторону по направлению катушки А к катушке В с угловой скоростью ωп, равной угловой частоте тока ω. В общем случае угловая скорость вращения магнитного поля зависит еще и от числа катушек: [рад/с] или [с-1].
[рад/с] или [с-1]. [об/мин].
[об/мин].



