
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Т.2. Теоремы и методы расчета сложных резистивных цепейСодержание книги
Поиск на нашем сайте
1. Основные определения
Узлом электрической цепи (схемы) называется точка, в которой сходятся не менее трех ветвей. Ветвью электрической цепи (схемы) называется участок, состоящий из последовательно включенных элементов, расположенных между двумя смежными узлами. Сложной называется электрическая цепь (схема), содержащая не менее двух узлов, не менее трех ветвей и не менее двух источников энергии в разных ветвях. В сложной электрической цепи наблюдаются одновременно в той или иной мере разнородные физические процессы, а именно, процесс генерирования электрической энергии, процесс преобразования электрической энергии в другие виды и процесс обмена энергией между магнитным полем, электрическим полем и источниками энергии. В общем случае для отображения этих физических процессов схема замещения цепи должна содержать кроме источников энергии (E, J) все разнородные схемные элементы (R, L, C). Математически физические процессы в такой схеме можно описать системой дифференциальных уравнений, составленных для схемы замещения по законам Кирхгофа. В стационарном режиме (в режиме постоянного тока) напряжение на катушке равно нулю ( В настоящей главе будут рассматриваться только резистивные цепи в режиме постоянного тока. В последующем рассмотренные в данной главе теоремы и методы расчета будут распространены на цепи переменного тока в установившемся синусоидальном режиме. 2. Метод преобразования (свертки) схемы
Если схема электрической цепи содержит только один источник энергии (E или J), то пассивная часть схемы может быть преобразована (свернута) к одному эквивалентному элементу R Э(рис. 7).
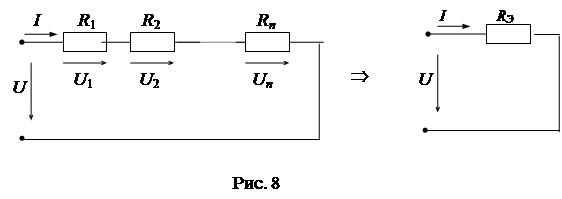
Свертка схемы начинается с самых удаленных от источника ветвей, проводится в несколько этапов до достижения полной свертки. После полной свертки схемы по закону Ома определяется ток источника: При применении данного метода возможны следующие виды преобразований. 1) Последовательное преобразование заключается в замене нескольких элементов, включенных последовательно, одним эквивалентным (рис. 8). Несложно доказать, что справедливы следующие соотношения:
2) Параллельное преобразование состоит в замене нескольких элементов, включенных параллельно, одним эквивалентным (рис. 9).
Несложно доказать, что справедливы следующие соотношения:
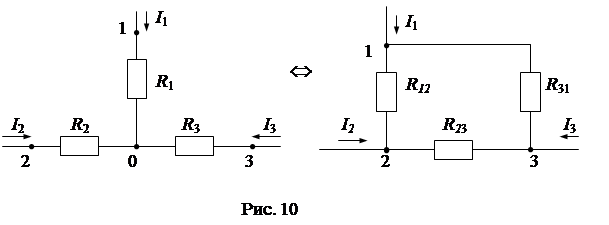
Для двух элементов: 3) Взаимное преобразование схем звезда-треугольник (рис. 4) возникает при свертке сложных схем. Условием эквивалентности двух схем являются равенства для них токов (I 1, I 2, I 3), напряжений (U 12, U 23, U 31) и входных сопротивлений (R 12, R 23, R 31) и соответственно входных проводимостей (G 12, G 23, G 31). Приравняем входные сопротивления для обеих схем со стороны двух произвольных ветвей при отключенной третей (рис. 10):
Сложим почленно уравнения (1) и (3) и вычтем из суммы уравнение (2), получим:
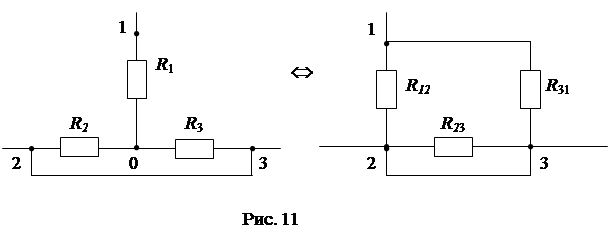
Приравняем входные проводимости для обеих схем со стороны произвольной вершины и двух других вершин, замкнутых накоротко (рис. 11):
Сложим почленно уравнения (4) и (5) и вычтем уравнение (6), получим:
В последних уравнениях заменим проводимости на соответствующие им сопротивления
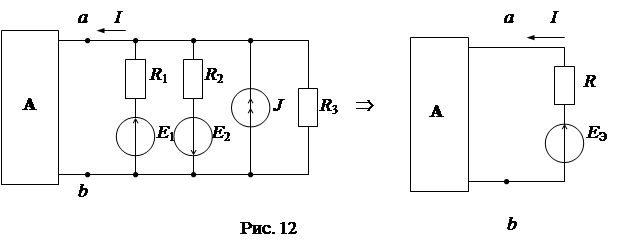
При наличии полной симметрии соотношение между параметрами эквивалентных схем составляет: 4) Замена параллельных ветвей эквивалентной ветвью (рис. 12) осуществляется согласно теореме об эквивалентном генераторе.
Напряжение холостого хода U xx aв =E Э определяется по методу двух узлов:
Эквивалентное входное сопротивление находится методом свертки схемы:
5) Перенос источника ЭДС через узел схемы: источник ЭДС Е можно перенести через узел во все ветви, отходящие от узла (рис. 13а, б.).
6) Привязка источника тока к произвольному узлу согласно схеме(рис. 14а, б):
7) Взаимное преобразование схем с источником напряжения и систочником тока согласно схеме(рис. 15а, б):
Схемы эквивалентны при равенстве для обеих напряжений U и токов I на нагрузке:
Сравнивая левые и правые части равенства, получим соотношения между параметрами эквивалентных схем:
Метод законов Кирхгофа
Теоретическая база метода: 1-й и 2-й законы Кирхгофа. 1-й закон Кирхгофа: алгебраическая сумма токов ветвей в узле схемы равна нулю ( 2-й закон Кирхгофа: алгебраическая сумма падений напряжений в произвольном контуре схемы равна алгебраической сумме ЭДС ( Пусть требуется выполнить расчет режима в заданной сложной схеме (рис. 16) и определить токи в ветвях, напряжения на отдельных элементах, мощности источников и приемников энергии. Задана схема цепи и параметры ее отдельных элементов (E 1, E 2, J 1, J 1, J 2, R 1, R 2, R 3, R 4, R 5).
Анализируем структуру схемы: схема содержит n =3 (0, 1, 2) узлов и m =5 ветвей с неопределенными токами. В ветвях с источниками тока J токи определены источниками. Общее число уравнений должно быть равно числу определяемых токов “ m ”. Последовательность (алгоритм) расчета. 1) Задаются (произвольно) положительными направлениями токов в ветвях схемы (I 1, I 2, I 3, I 4, I 5). 2) Составляется (n -1) уравнений для узлов по первому закону Кирхгофа. Уравнение для последнего n -го узла является зависимым (оно может быть получено путем сложения первых (n -1) уравнений). 3) Недостающие m -(n -1) уравнений составляются по 2-му закону Кирхгофа. Правило выбора контуров для составления уравнений: каждый последующий контур должен включать в себя хотя бы одну новую ветвь, не охваченную предыдущими уравнениями. Число независимых контуров для схемы любой сложности не может быть больше числа m -(n -1). Ниже приведена система уравнений Кирхгофа для схемы рис. 16, состоящая из m =5 уравнений, из которых n -1=2 составлены для узлов 1 и 2 по 1-му закону Кирхгофа и m -(n -1)=3 составлены для контуров К1, К2, К3 по 2-му закону Кирхгофа:
4) Система уравнений приводится к матричной форме, составляются матрицы коэффициентов:
5) Система уравнений решается на ЭВМ по стандартной программе для решения линейных алгебраических уравнений с вещественными коэффициентами (SU1), в результате чего определяются неизвестные токи I 1, I 2, I 3, I 4, I 5. Отрицательные результаты, получаемые для некоторых токов, означают, что их действительные (физические) направления не соответствуют направлениям, принятым в начале расчета. 6) Определяются напряжения на отдельных элементах схемы (
Теоретическая база метода контурных токов – 2-ой закон Кирхгофа в сочетании с принципом наложения. Предполагают, что в каждом элементарном контуре-ячейке схемы протекает «свой» контурный ток Ik, а действительные токи ветвей получаются по принципу наложения контурных токов как их алгебраические суммы. В качестве неизвестных величин, подлежащих определению, в данном методе выступают контурные токи. Общее число неизвестных составляет m -(n -1). Пусть требуется выполнить расчет режима в заданной сложной схеме рис. 11. Параметры отдельных элементов схемы заданы. Последовательность (алгоритм) расчета. 1) Задаются (произвольно) положительными направлениями контурных токов в контурах-ячейках схемы(Iк 1, Iк 2, Iк 3 ). Контуры-ячейки следует выбирать так, чтобы они не включали в себя ветви с источниками тока. Ветви с источниками тока J образуют свои контуры с заданными токами (J 1, J 2). 2) Составляются m -(n -1) уравнений по 2-му закону Кирхгофа для выбранных контуров-ячеек с контурными токами Iк 1, Iк 2, Iк 3. В уравнениях учитываются падения напряжений как от собственного контурного тока, так и от смежных контурных токов.
Ниже приведена система контурных уравнений для схемы рис. 17:
Здесь введены следующие обозначения: R 11= R 1 + R 4; R 22 = R 2 + R 5 и т. д. – собственные сопротивления контуров, равные сумме сопротивлений всех элементов контура; R 12 = R 21 = 0; R 23 = R 32 = - R 5 и т. д. – взаимные сопротивления между двумя смежными контурами, они положительны – если контурные токи в ветви совпадают, и отрицательны – если контурные токи в ветви направлены встречно, всегда отрицательны – если все контурные токи ориентированы одинаково (например, по часовой стрелке), равны нулю – если контуры не имеют общей ветви; E 11 = E 1 + J 1 R 4, E 22 = - E 2, E 33 = - E 3 + J 2 R 3 и т. д. – контурные ЭДС, равные алгебраической сумме слагаемых E nn = S E + S JR от всех источников контура. Система контурных уравнений в матричной форме:
где 3) Система контурных уравнений решается на ЭВМ по стандартной программе для решения систем линейных алгебраических уравнений с вещественными коэффициентами (SU1), в результате чего определяются неизвестные контурные токи Iк 1, Iк 2, Iк 3. 4) Выбираются положительные направления токов в ветвях исходной схемы (рис. 1) (I 1, I 2, I 3, I 4, I 5). Токи ветвей определяются по принципу наложения как алгебраические суммы контурных токов, протекающих в данной ветви.
I 1 = Iк 1 - J 1; I 2 = - Iк 2; I 3 = - Iк 3 – J 2; I 4 = Iк 1 – Ik 3; I 5 = - Iк 2 + Ik 3 . 5) При необходимости определяются напряжения на отдельных элементах (Uk = IkRk), мощности источников энергии (PEk = EkIk, PJk = Uk Jk) и приемников энергии (Pk = Ik 2 × Rk).
5. Метод узловых потенциалов
Теоретическая база метода узловых потенциалов – 1-ый закон Кирхгофа в сочетании с потенциальными уравнениями ветвей. В этом методе потенциал одного из узлов схемы принимают равным нулю, а потенциалы остальных (n -1) узлов считают неизвестными, подлежащими определению. Общее число неизвестных составляет (n -1). Рассмотрим обобщенную ветвь некоторой сложной схемы (рис. 18).
Свяжем потенциалы концов ветви (узлов) между собой через падения напряжений на отдельных участках:
Уравнение, связывающее потенциалы конечных точек ветви через падения напряжений на ее отдельных участках, называется потенциальным уравнением ветви. Из потенциального уравнения ветви могут быть определены ток ветви и напряжение на резисторе:
Пусть требуется выполнить расчет режима в заданной сложной схеме рис. 19. Параметры отдельных элементов схемы заданы. Принимаем потенциал узла 0 равным нулю (j 0 = 0), а потенциалы узлов 1 и 2 (j 1 и j 2) будем считать неизвестными, подлежащими определению. Зададимся положительными направлениями токов в ветвях схемы I 1, I 2, I 3, I 4, I 5. Составим потенциальные уравнения ветвей и выразим из них токи ветвей: I 1 = (j 1 – j 0 + E 1 )/ R 1 I 2 = (j 2 – j 0 + E 2 )/ R 2 I 3 = (j 1 – j 0 + E 3 )/ R 3 I 4 = (j 0 – j 1 )/ R 4 I 5 = (j 0 - j 2 )/ R 5
Составим (n -1) уравнение по 1-му закону Кирхгофа для узлов 1 и 2: - I 1 – I 3 + I 4 – J 1 – J 2 = 0 - I 2 + I 3 + I 5 + J 2 =0 Подставим значения токов из потенциальных уравнений в уравнения 1-го закона Кирхгофа. После приведения коэффициентов получим систему узловых уравнений:
В обобщенной форме система узловых уравнений имеет вид:
Здесь введены следующие обозначения: G 11 =1/ R 1 +1/ R 3 +1/R4; G 22 =1/ R 2 +1/ R 3 +1/ R 5 и т.д. – собственные проводимости узлов, равные суммам проводимостей всех ветвей, сходящихся в данном узле, всегда положительны; G 12 = G 21 = 1/ R 3; Gnm = Gm n– взаимные проводимости между смежными узлами (1 и 2, m и n), равные сумме проводимостей ветвей, соединяющих эти узлы, всегда отрицательны; J 11 = - E 1 / R 3 – E 3 / R 3 – J 1; J 11 =- E 2 / R 2 – E 3 / R 3 + J 1 и т.д. – узловые токи узлов, равные алгебраической сумме слагаемых E/R и J от всех ветвей, сходящихся в узле (знак ”+”, если источник действует к узлу, и знак “-”, если источник действует от узла). Система узловых уравнений в матричной форме:
где Последовательность (алгоритм) расчета. 1) Принимают потенциал одного из узлов схемы равным нулю, а потенциалы остальных (n -1) узла считают неизвестными, подлежащими определению. 2) Руководствуясь обобщенной формой, составляют (n -1) уравнение для узлов с неизвестными потенциалами.
3) Определяются коэффициенты узловых уравнений и составляются их матрицы. 4) Система узловых уравнений решается на ЭВМ по стандартной программе для решения систем линейных алгебраических уравнений с вещественными коэффициентами (SU1), в результате чего определяются неизвестные потенциалы узлов j 1, j 2, … 5) Выбираются положительные направления токов в ветвях исходной схемы I 1, I 2, I 3, I 4, I 5. Токи ветвей определяются из потенциальных уравнений ветвей через потенциалы узлов j 1, j 2, …. 6) При необходимости определяются напряжения на отдельных элементах (Uk = IkRk), мощности источников энергии (PEk = EkIk, PJk = Uk Jk) и приемников энергии (Pk = Ik 2 × Rk).
6. Метод двух узлов
Метод двух узлов является частным случаем метода узловых потенциалов при числе узлов в схеме n = 2 (рис. 20).
Принимаем j 0 = 0, тогда уравнение для узла 1 по методу узловых потенциалов будет иметь вид: j 1 G 11 = J 11, откуда следует непосредственное определение напряжения между узлами схемы:
Применительно к схеме рис. 20 данное уравнение примет конкретную форму:
7. Принцип наложения. Метод наложения Принцип (теорема) наложения гласит, что ток в любой ветви (напряжение на любом элементе) сложной схемы, содержащей несколько источников, равен алгебраической сумме частичных токов (напряжений), возникающих в этой ветви (на этом элементе) от независимого действия каждого источника в отдельности. Для упрощения доказательства теоремы выберем одну из наружных ветвей сложной схемы за номером 1, в которой действительный ток равен контурному: I 1 = Ik 1. Составим для сложной схемы систему контурных уравнений
Здесь G 11 –входная проводимость ветви 1, G 12, G 13, …, G 1n– взаимные проводимости между 1-й и остальными ветвями, I 11 = E 1 G 11 – частичный ток в ветви 1 от источника ЭДС E 1, I 12 = E 2 G 12, …, I 1n = E n G 1n – частичные токи в ветви 1 от источников ЭДС E 2,…, En. Принцип наложения выполняется только для тех физических величин, которые описываются линейными алгебраическими уравнениями, например, для токов и напряжений в линейных цепях. Принцип наложения не выполняется для мощности, которая с током связана нелинейным уравнением P=I 2 ×R. Принцип наложения лежит в основе метода расчета сложных цепей, получившего название метода наложения. Сущность этого метода состоит в том, что в сложной схеме с несколькими источниками последовательно рассчитываются частичные токи от каждого источника в отдельности. Расчет частичных токов выполняют, как правило, методом преобразования схемы. Действительные токи определяются путем алгебраического сложения частичных токов с учетом их направлений.
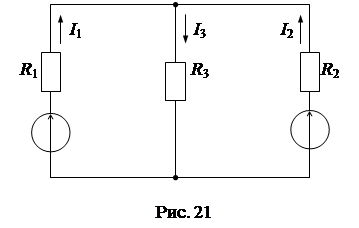
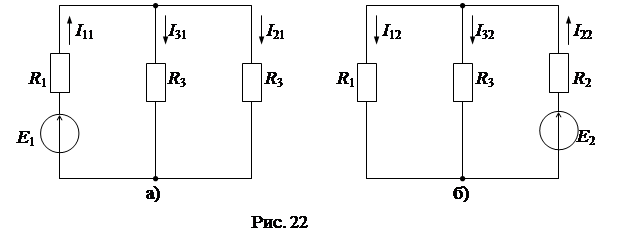
На рис. 22а представлена схема цепи для определения частичных токов от источника ЭДС Е 1, а на рис. 22б - от источника ЭДС Е 2.
Частичные токи в схеме рис. 22а от E1:
Частичные токи в схеме рис. 22б от E2:
Действительные токи как алгебраические суммы частичных токов: I 1 = I 11 - I 12 = 4 – 1,5 = 2,5 A I 2 = - I 21 + I 22 = -2 + 3 =1 A I 3 = I 31+ I32 = 2 + 1,5 =3,5 A 8. Теорема о взаимности
Выделим из сложной схемы две произвольные ветви “ m ” и “ n ”, в одной из которых включен источник ЭДС E (в ветви m). Теорема о взаимности гласит, что если источник ЭДС E, включенный в ветви “ m ”, вызывает в ветви “ n ” частичный ток I, то такой же источник ЭДС E, включенный в ветвь “ n ”, вызовет в ветви “ m ” такой же частичный ток I (рис.23).
Доказательство теоремы о взаимности вытекает из принципа наложения. Частичные токи равны:
Так как взаимные проводимости в линейной цепи равны (Gmn=Gnm), то соответственно равны токи в обеих схемах.
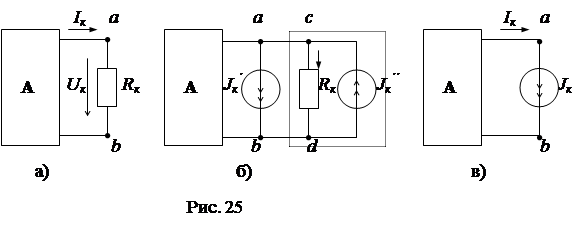
Теорема о компенсации Формулировка теоремы: любой пассивный элемент электрической схемы можно заменить а) идеальным источником напряжения с ЭДС, равной напряжению на этом элементе (E = U) и направленной навстречу току, б) идеальным источником тока J, равным току в этом элементе (J = I) и направленным согласно току I.
Выделим пассивный элемент Rk с током Ik и напряжением Uk из схемы цепи (рис. 24а). Для доказательства п. а) теоремы включим последовательно с элементом Rk навстречу друг другу два идеальных источника ЭДС
Точки “ a ” и “ d ”, как точки равного потенциала, можно закоротить и закороченный участок “ a-d ” из схемы удалить без нарушения ее режима. В результате удаления закороченного участка схема получает вид рис. 24в, в которой пассивный элемент Rk заменен идеальным источником ЭДС
Для доказательства п. б) теоремы включим параллельно с элементом Rk два идеальных источника тока Такое включение источников тока
10. Теорема о линейных отношениях
Формулировка теоремы: если в произвольной к -ой ветви сложной схемы изменяется ЭДС источника Ek или сопротивление резистора Rk, то параметры режима в двух других ветвях (например, 1 и 2, I 1 и I 2, U 1 и U 2, U 1 и I 2, I 1 и U 2 ) изменяются так, что между ними сохраняется линейная зависимость ( Пусть изменяется ЭДС Eк. В соответствии с принципом наложения ток каждой ветви равен сумме частичных токов от каждого источника в отдельности:
Исключим из уравнений переменную величину E к путем подстановки:
Если в схеме изменяется сопротивление резистора
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 556; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.2.209 (0.013 с.) |

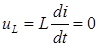 ), что соответствует короткому замыканию этого элемента, а при постоянном напряжении ток в конденсаторе равен нулю (
), что соответствует короткому замыканию этого элемента, а при постоянном напряжении ток в конденсаторе равен нулю (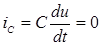 ), что соответствует разрыву ветви с этим элементом. Следовательно, на установившийся режим постоянного тока схемные элементы L и C не оказывают влияния и могут быть исключены из схемы замещения (участки с L закорочены, а ветви с C удалены). Цепи постоянного тока представляются эквивалентными схемами, содержащими только постоянные источники энергии E, J и резистивные элементы R. Такие схемы получили название резистивных или постоянного тока. Установившийся режим постоянного или переменного тока в таких схемах описывается системой линейных алгебраических уравнений, составленных по законам Кирхгофа.
), что соответствует разрыву ветви с этим элементом. Следовательно, на установившийся режим постоянного тока схемные элементы L и C не оказывают влияния и могут быть исключены из схемы замещения (участки с L закорочены, а ветви с C удалены). Цепи постоянного тока представляются эквивалентными схемами, содержащими только постоянные источники энергии E, J и резистивные элементы R. Такие схемы получили название резистивных или постоянного тока. Установившийся режим постоянного или переменного тока в таких схемах описывается системой линейных алгебраических уравнений, составленных по законам Кирхгофа.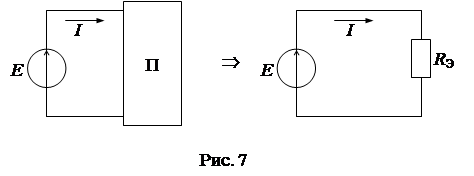
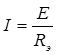 . Токи в остальных элементах исходной схемы находятся в процессе обратной развертки схемы. Такой метод расчета токов получил название метода последовательного преобразования (свертки) схемы.
. Токи в остальных элементах исходной схемы находятся в процессе обратной развертки схемы. Такой метод расчета токов получил название метода последовательного преобразования (свертки) схемы.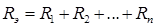 и
и 

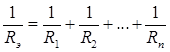 и
и 
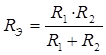 и
и 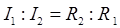
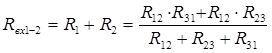 (1)
(1)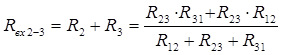 (2)
(2)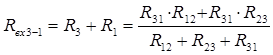 (3)
(3)
 , по аналогии:
, по аналогии: 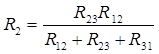 ,
,  .
.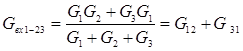 (4)
(4)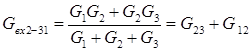 (5)
(5)
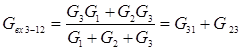 (6)
(6) , по аналогии:
, по аналогии: 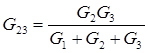 ,
, 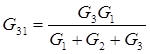 .
. , получим:
, получим: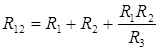 ;
;  ;
;  .
.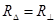 .
.
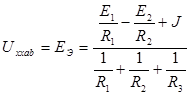 .
. .
.


 .
. .
. ).
).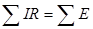 ).
).

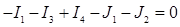 - узел 1,
- узел 1,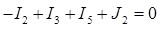 - узел 2,
- узел 2,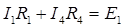 - контур К1,
- контур К1,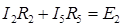 - контур К2,
- контур К2,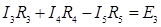 - контур К3.
- контур К3. ;
; 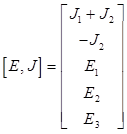
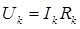 ), мощности источников ЭДС (
), мощности источников ЭДС (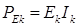 ),источников тока (
),источников тока (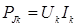 ) и приемников (
) и приемников (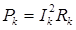 ). При этом мощности приемников энергии всегда положительны, а мощности источников энергии могут быть отрицательными, если сомножители в произведениях
). При этом мощности приемников энергии всегда положительны, а мощности источников энергии могут быть отрицательными, если сомножители в произведениях 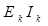 и
и 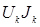 не совпадают по направлению.
не совпадают по направлению. 4. Метод контурных токов
4. Метод контурных токов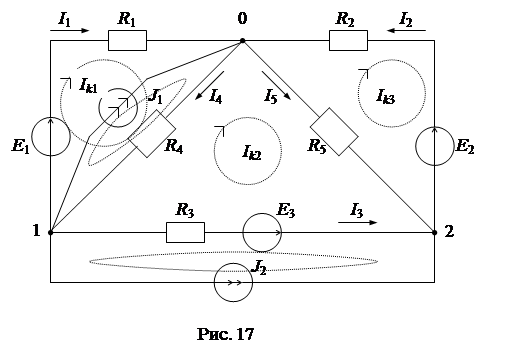

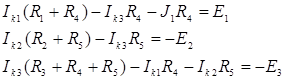
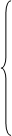 В обобщенной форме система контурных уравнений имеет вид:
В обобщенной форме система контурных уравнений имеет вид: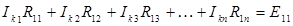
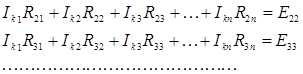
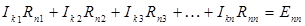
 или в сокращенно
или в сокращенно 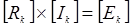 ,
, - матрица контурных сопротивлений,
- матрица контурных сопротивлений,  - матрица контурных токов,
- матрица контурных токов, 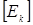 - матрица контурных ЭДС.
- матрица контурных ЭДС.
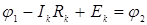 или
или 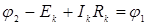
 ,
, 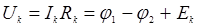 .
.
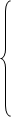
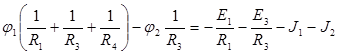


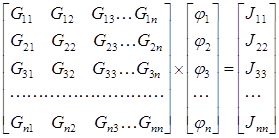 или сокращенно
или сокращенно 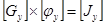 ,
,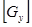 - матрица узловых проводимостей,
- матрица узловых проводимостей,  - матрица узловых потенциалов,
- матрица узловых потенциалов, 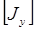 - матрица узловых токов.
- матрица узловых токов.
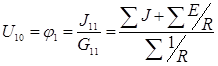 - уравнение метода двух узлов.
- уравнение метода двух узлов.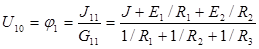
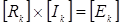 и решим ее относительно тока I 1 = Ik 1 методом определителей (Крамера):
и решим ее относительно тока I 1 = Ik 1 методом определителей (Крамера):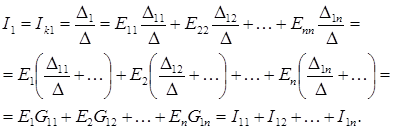
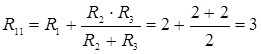 Ом; I 11 = E 1 /R 11 = 12/3 = 4A; I 21 = I 31 = 2А.
Ом; I 11 = E 1 /R 11 = 12/3 = 4A; I 21 = I 31 = 2А.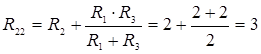 Ом; I 22 = E 2 /R 22 = 9/3 = 3A; I 12 = I 32 = 1,5А.
Ом; I 22 = E 2 /R 22 = 9/3 = 3A; I 12 = I 32 = 1,5А.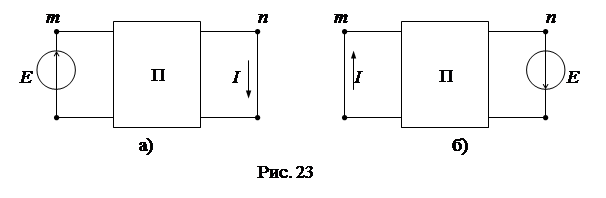
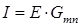 — для схемы рис. 23а,
— для схемы рис. 23а, 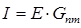 — для схемы рис. 23б.
— для схемы рис. 23б.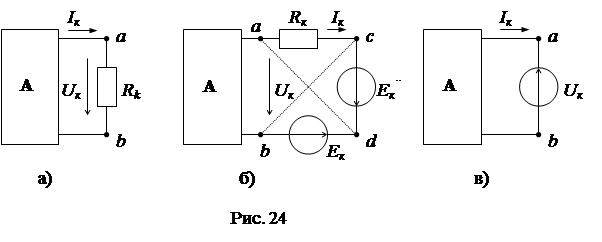
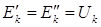 (рис. 24б). Такое включение источников ЭДС не вызовет изменения режима сложной схемы, так как их действие взаимно компенсируется. Cоставим потенциальное уравнение между точками “a” и “d”:
(рис. 24б). Такое включение источников ЭДС не вызовет изменения режима сложной схемы, так как их действие взаимно компенсируется. Cоставим потенциальное уравнение между точками “a” и “d”: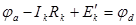 , откуда следует
, откуда следует 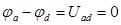 , или
, или 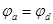
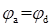 .
.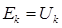 .
.
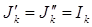 , направленные навстречу друг другу (рис. 25б).
, направленные навстречу друг другу (рис. 25б).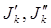 не вызовет изменения режима сложной схемы, так как их действия взаимно компенсируются. С другой стороны ток в ветви “ a-c ” равен нулю (
не вызовет изменения режима сложной схемы, так как их действия взаимно компенсируются. С другой стороны ток в ветви “ a-c ” равен нулю (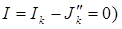 , и эту ветвь можно отключить без нарушения режима остальной части схемы. В результате отключения схема получает вид рис. 25в, в которой пассивный элемент Rk заменен идеальным источником тока Jk=Ik.
, и эту ветвь можно отключить без нарушения режима остальной части схемы. В результате отключения схема получает вид рис. 25в, в которой пассивный элемент Rk заменен идеальным источником тока Jk=Ik.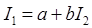 и т.д.).
и т.д.).
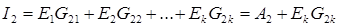
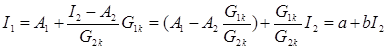 , что требовалось доказать.
, что требовалось доказать. , то для доказательства теоремы о линейных отношениях переменный резистор
, то для доказательства теоремы о линейных отношениях переменный резистор 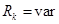 следует заменить в соответствии с теоремой о компенсации переменной ЭДС
следует заменить в соответствии с теоремой о компенсации переменной ЭДС  и повторить доказательство.
и повторить доказательство.


