
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы соединения фаз трехфазных приемников.Содержание книги
Поиск на нашем сайте
Приемники трехфазного тока могут подключаться к генератору по двум схемам – звезды ( Схема звезды применяется в том случае, если номинальное напряжение приемника соответствует (равно) фазному напряжению генератора. При соединении в звезду концы фаз приемника объединяются в одну точку “ n ”, называемую нулевой или нейтральной, а начала фаз подключаются к линейным выводам трехфазного генератора А, В, С линейными проводами. Если нулевая точка приемника “ n ” соединена с нулевой точкой генератора “ N ” нулевым проводом, то схема получила название звезды с нулевым проводом (рис. 91а). При отсутствии нулевого провода схема носит название звезды без нулевого провода (рис. 91б). Токи, протекающие в линейных проводах по направлению от генератора к приемнику, называются линейными. Токи, протекающие в фазах приемника по направлению от начал к концам, называются фазными. В схеме звезды фазы приемника включены последовательно с линейными проводами и по ним протекают одни и те же токи (I A, I B, I C). Поэтому для схемы звезды понятия линейные и фазные токи тождественны: IЛ = IФ. Ток, протекающий в нулевом проводе от приемника к генератору, называется нулевым или нейтральным (I N).
Напряжения между началами и концами фаз приемника называются фазными (U An, U Bn, U Cn), а напряжения между началами фаз – линейными (U AB, U BC, U CA). Линейные напряжения приемника и генератора тождественно равны. В схеме звезды с нулевым проводом (рис. 91а) к каждой фазе приемника подводится непосредственно фазное напряжение генератора (U AN = U An = U A, U BN = U Bn = U B, U CN = U Cn = U C), каждая из фаз при этом работает независимо друг от друга, а линейные (фазные) токи определяются по закону Ома:
Ток в нулевом проводе в соответствии с первым законом Кирхгофа равен геометрической сумме линейных (фазных) токов:
Пример. Исходные данные: U Л ⁄ U Ф = 380 ⁄ 220 В, Z A = 100ej35 Ом, Z В = 110ej20 Ом, Z С = 140ej35 Ом. Определить линейные (фазные) токи I A, I B, I C и ток в нулевом проводе I N.
Векторная диаграмма токов и напряжений показана на рис. 92.
При симметричной нагрузке При несимметричной нагрузке относительная величина тока в нулевом проводе зависит от характера и степени не симметрии фазных токов. Как правило, трехфазные приёмники стремятся спроектировать по возможности близкими к симметричным, поэтому ток в нулевом проводе в реальных условиях значительно меньше линейных (фазных) токов. В схеме звезды без нулевого провода (рис. 91б) при любой нагрузке фаз должно выполняться условие первого закона Кирхгофа:
Из уравнения следует вывод, что изменение одного из токов влечет изменение двух других токов, то есть отдельные фазы работают в зависимом друг от друга режиме. При несимметричной нагрузке потенциал нулевой точки приемника U n становится не равным нулю, он “смещается” на комплексной плоскости с нулевого положения, при этом фазные напряжения приемника (
Расчет токов и напряжений в схеме звезды без нулевого провода выполняется в следующей последовательности. Определяется напряжение (потенциал) нейтральной точки приемника по методу двух узлов:
где Z N - комплексное сопротивление нулевого провода, при его отсутствии Z N= ¥. Фазные напряжения приемника определяются как разности потенциалов соответствующих точек:
Фазные токи приемника определяются по закону Ома:
Комплексные мощности фаз приемника:
Режим работы приемника с перекосом фазных напряжений является ненормальным и может привести его к выходу из строя. По этой причине несимметричную трехфазную нагрузку запрещается включать по схеме звезды без нулевого провода (например, осветительную нагрузку).
Схема треугольника применяется в том случае, если номинальное фазное напряжение приемника соответствует (равно) линейному напряжению генератора. При соединении в треугольник конец каждой фазы соединяется с началом последующей, а точки соединения (вершины треугольника) подключаются к линейным выводам трехфазного генератора А, В, С линейными проводами (рис.94). Токи, протекающие в фазах приемника по направлению от их начал к концам, называются фазными (
В схеме треугольника фазные и линейные напряжения приемника тождественно равны (
Линейные токи определяются из уравнений первого закона Кирхгофа для вершин треугольника, они равны геометрической разности фазных токов:
В симметричном режиме ( При несимметричной нагрузке соотношение между линейными и фазными токами определяется уравнениями первого закона Кирхгофа. На рис. 95 показана векторная диаграмма токов и напряжений для произвольной трехфазной цепи при соединении фаз в треугольник.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.224 (0.009 с.) |

 ) и треугольника (
) и треугольника ( ). Как известно, на выходе трехфазного генератора получаются два напряжение (линейное и фазное), отличающиеся в U л/ U ф =
). Как известно, на выходе трехфазного генератора получаются два напряжение (линейное и фазное), отличающиеся в U л/ U ф =  раз. С другой стороны каждый приёмник энергии рассчитан на работу при определенном напряжении, которое называется номинальным. Схема соединения фаз приемника должна обеспечить подключение его фаз номинальное фазное напряжение. Таким образом, выбор схемы соединения фаз трехфазного приемника зависит от соотношения номинальных напряжений приемника и генератора (сети).
раз. С другой стороны каждый приёмник энергии рассчитан на работу при определенном напряжении, которое называется номинальным. Схема соединения фаз приемника должна обеспечить подключение его фаз номинальное фазное напряжение. Таким образом, выбор схемы соединения фаз трехфазного приемника зависит от соотношения номинальных напряжений приемника и генератора (сети).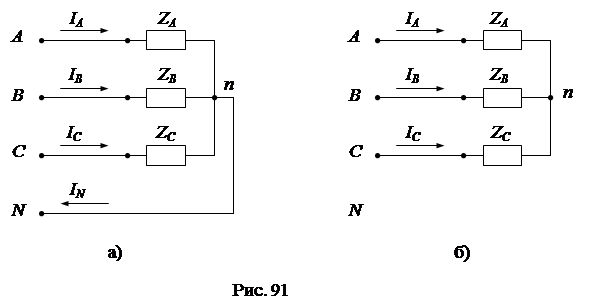
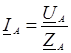 ;
;  ;
; 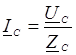 .
. .
. А,
А, А,
А, А,
А,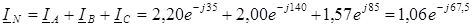 A.
A.
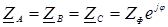 ток в нулевом проводе
ток в нулевом проводе  и, следовательно, надобность в нeм отпадает. Симметричные трехфазные приемники (например, трехфазные электродвигатели) включаются по схеме звезды без нулевого провода.
и, следовательно, надобность в нeм отпадает. Симметричные трехфазные приемники (например, трехфазные электродвигатели) включаются по схеме звезды без нулевого провода. .
. ) не равны соответствующим фазным напряжениям генератора (
) не равны соответствующим фазным напряжениям генератора ( ), происходит так называемый перекос фазных напряжений приемника (рис. 93).
), происходит так называемый перекос фазных напряжений приемника (рис. 93).
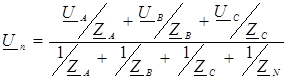 ,
, ,
, 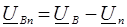 ,
,  .
.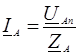 ;
; 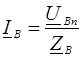 ;
; 
 ,
,  ,
,  .
. ). Токи, протекающие в линейных проводах по направлению от генератора к приемнику, называются линейными (
). Токи, протекающие в линейных проводах по направлению от генератора к приемнику, называются линейными ( ).
).
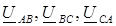 ). В этой схеме к каждой фазе приемника подводится непосредственно линейное напряжение генератора, при этом отдельные фазы работают независимо друг от друга. Фазные токи определяются по закону Ома:
). В этой схеме к каждой фазе приемника подводится непосредственно линейное напряжение генератора, при этом отдельные фазы работают независимо друг от друга. Фазные токи определяются по закону Ома: ;
;  ;
;  .
. ;
;  ;
;  .
.
 .
.



