
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретические основы метода симметричных составляющихСодержание книги
Поиск на нашем сайте
Метод симметричных составляющих применяется для расчета трехфазных цепей в несимметричных режимах. Несимметричные режимы в энергосистеме возникают при различных видах коротких замыканий. Расчет токов коротких замыканий – важная инженерная задача в электроэнергетике, которая решается методом симметричных составляющих. Математически любая несимметричная трехфазная система векторных величин (напряжений, токов и др.) может быть представлена в виде суммы (заменена суммой) из трех симметричных трехфазных систем, а именно: а) системы прямой последовательности с прямым порядком следования фаз A→B→C→A; б) системы обратной последовательности с обратным порядком следования фаз A→C→B→A; в) системы нулевой последовательности, которая состоит из трех равных векторов, совпадающих по фазе. Отдельные симметричные системы векторов, на которые раскладывается несимметричная система, называются симметричными составляющими. Вектора симметричных составляющих индексируются цифрами: 1 - для прямой последовательности, 2 - для обратной последовательности и 0 – для нулевой последовательности. На рис. 1 представлены симметричные составляющие некоторой несимметричной трехфазной системы напряжений U A, U B, U C. В методе симметричных составляющих для упрощения формы записи уравнений пользуются коэффициентом
Вектора исходной несимметричной системы определяются по принципу наложения как геометрические суммы соответствующих векторов симметричных составляющих:
Геометрическое сложение векторов симметричных составляющих согласно этим уравнениям показано на рис. 107. Используя поворотный множитель “ a ” и “ a 2”, выразим все слагаемые правой части уравнений через симметричные составляющие фазы А:
 
Умножим все члены уравнения (2) на “ a ”, а все члены уравнения (3) на “ a 2”, сложим все три уравнения почленно и получим:
Из полученного уравнения следует формула для выделения симметричной составляющей прямой последовательности из несимметричной системы векторов:
Умножим все члены уравнения (2) на “ a 2”, а все члены уравнения (3) на “ a ”, сложим все три уравнения почленно и получим:
Из полученного уравнения следует формула для выделения симметричной составляющей обратной последовательности из несимметричной системы векторов:
Сложим все три уравнения (1), (2) и (3) почленно и получим:
Из полученного уравнения следует формула для выделения симметричной составляющей нулевой последовательности из несимметричной системы вектор:
Полученные формулы применяются на практике для разложения несимметричных трехфазных систем векторов на симметричные составляющие.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.116.145 (0.007 с.) |

 (поворотный множитель), умножением на который поворачивают вектор на угол в 1200 без изменения его модуля. Свойства поворотного множителя:
(поворотный множитель), умножением на который поворачивают вектор на угол в 1200 без изменения его модуля. Свойства поворотного множителя: 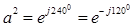 ,
,  ,
,  ,
,  .
.


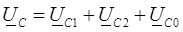
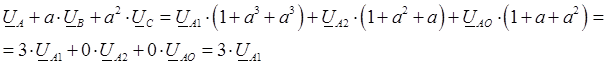

 .
.
 .
. .
.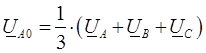 .
.


