
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множества и бинарные отношенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. При голосовании в городскую думу в бюллетене в списке из трех кандидатов требовалось оставить не более одного. При подведении итогов оказалось, что кандидатов 2. Сколько бинарных отношений можно определить на множестве из 3. На множестве 4. Рассмотрим на множестве действительныхчисел
Выяснить, какими свойствами обладают перечисленные бинарные отношения. 5. Приведите пример рефлексивного, транзитивного, но не симметричного бинарного отношения на множестве из 4-х элементов. 6. Приведите пример рефлексивного, симметричного, но не транзитивного бинарного отношения на множестве из 4-х элементов. 7. Приведите пример транзитивного, симметричного, но не рефлексивного бинарного отношения на множестве из 4-х элементов. 8. Пусть Что представляет собой матрица отношений а) рефлексивно; б) симметрично; г) антисимметрично. 9. Пусть 10. Доказать, что если бинарное отношение одновременно симметрично и антисимметрично, то оно транзитивно. 11. а) Сколько существует рефлексивных бинарных соотношений на множестве из б) Сколько существует симметричных бинарных соотношений на множестве из в) Сколько существует антисимметричных бинарных соотношений на множестве из Контрольная работа 3. 1. Граф задан множеством вершин и ребер: а) построить диаграмму;
б) указать какой-либо путь, не являющийся цепью; какую-либо цепь, не являющуюся простой цепью; цикл, не являющийся простым; простой цикл (в каждом варианте что-нибудь одно). 2. Для данного графа найти: а) цикломатическое число; б) хроматическое число. 3. Построить граф (или орграф) по матрице смежности или инцидентности или, наоборот, найти матрицу смежности или инцидентности графа. 4. Написать код дерева (в одних вариантах бинарный, в других – из натуральных чисел). 5. Построить дерево по коду (в одних вариантах по бинарному, в других – из натуральных чисел). 6. Построить на связном графе остов минимального веса, указать его вес. Контрольная работа рассчитана на 30-40 минут. Образцы вариантов контрольной работы 3.
Структуры варианта БДЗ 1. Используя теорему Кирхгофа, найти число остовов в обыкновенном графе 2. Найти базис циклов на графе (граф задан матрицей инцидентности). 3. Найти эйлерову цепь (цикл) на графе
4. С помощью алгоритма Дейкстры найти расстояния от вершины 5. С помощью алгоритма Форда-Фалкерсона найти максимальный поток и минимальный разрез в сети Образец варианта БДЗ 1. Используя теорему Кирхгофа, найти число остовов в обыкновенном графе 2. Найти базис циклов на графе, заданном матрицей инцидентности
3. Найти эйлерову цепь на графе с вершинами 1,2,3.4.5,6,7.8,9 и ребрами 4. С помощью алгоритма Дейкстры найти расстояния от вершины 3 ориентированного графа 5. С помощью алгоритма Форда-Фалкерсона найти максимальный поток и минимальный разрез в сети
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.50.94 (0.009 с.) |

 и
и  вычеркнули 60% избирателей, кандидатов
вычеркнули 60% избирателей, кандидатов  - 80% избирателей, а кандидатов
- 80% избирателей, а кандидатов  элементов?
элементов? задано бинарное отношение
задано бинарное отношение  . Какими свойствами это бинарное отношение обладает? Является ли оно отношением эквивалентности? порядка? В том случае, если
. Какими свойствами это бинарное отношение обладает? Является ли оно отношением эквивалентности? порядка? В том случае, если  - отношение эквивалентности, указать разбиение множества
- отношение эквивалентности, указать разбиение множества  бинарные отношения
бинарные отношения  , определенные условиями:
, определенные условиями: ,
,  ,
,  ,
,  .
. - конечное множество. Сопоставим каждому бинарному отношению
- конечное множество. Сопоставим каждому бинарному отношению  на
на  матрицу размера
матрицу размера  , называемую матрицей отношения, в которой на пересечении
, называемую матрицей отношения, в которой на пересечении  -й строки и
-й строки и  -го столбца стоит 1. если
-го столбца стоит 1. если  и 0 в противном случае.
и 0 в противном случае. бинарное отношение
бинарное отношение  :
:  (здесь
(здесь  ,
,  ). Является ли отношение
). Является ли отношение  - граф с вершинами
- граф с вершинами  и ребрами
и ребрами  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 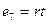 .
а) Построить диаграмму графа
.
а) Построить диаграмму графа  .
.
 и множеством ребер
и множеством ребер  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
а) Построить диаграмму графа
.
а) Построить диаграмму графа 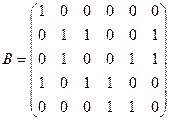 .
.


 ориентированного графа
ориентированного графа  (граф задан списком дуг и весовым отображением).
(граф задан списком дуг и весовым отображением). . Нарисовать диаграммы нескольких остовов.
. Нарисовать диаграммы нескольких остовов. .
. ,
,  ,
,  ,
, ,
,  ,
,  , а расстояние между вершинами определяется как сумма их номеров.
, а расстояние между вершинами определяется как сумма их номеров.


