
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямое произведение множеств. Отношения, бинарные отношения. Операции над отношениями.Содержание книги
Поиск на нашем сайте
Прямое произведение множеств. Отношения, бинарные отношения. Операции над отношениями. Прямым произведением множеств X u Y называется множество, состоящее из всех тех и только тех пар, первая компонента которой X*Y Пример: X = {a,b} Y = {1,2,3} X*Y={<a,1>,<a,2>,<a,3>,<b,1>,<b,2>,<b,3>} X*Y (*) X1,X2,…Xn Прямым произведением множества (*) называется множество, состоящее из всех тех и только тех картежей длины l, первая компонента которой Отношения, бинарные отношения. Рассмотрим вспомогательное понятие картеж. Упорядоченная пара <x,y> интуитивно определяется, как совокупность, состоящая из 2-х элементов х Две пары <x,y> u <U,V> равны тогда и только тогда, когда x=U, y=V <1,z> Картеж или упорядоченный набор n элементов x1 Два картежа
x2=y2 Число n – называется длинной картежа, а элементы xi – итой проэкцией (координата компоненты картежа). Операции над отношениями. 1. Для бинарных отношений обычным образом определены все теоретико-множественные операции: 2. Обратное отношение: обратным (инверсным) отношением называется отношение
3. Композиция отношений: а)
Композицией двух бинарных отношений
б) Композиция отношений на множестве X:
Замечание: Композиция отношений на множестве X порождает понятие: степень отношения
Понятие функции. Инъективные, биективные, суръективные функции. Композиция и обращение функций. Бинарное отношение f называется функцией, если <x,y> Замечание: 1) Если Df=X,а Rf f:X 2)Если f функция, то вместо <x,y> Lx={<x,x>| x Пусть задана f: x -Функция (отображение f) называется инъективной, если
-Функция называется суръективной, если для всякого y существует такое х, что y=f(x) -Функция называется биективной, если f одновременно: инъективна и суръективна. Замечание: Если существуeт функция f: x Можно доказать следующие утверждения: - композиция 2-х функций, есть функция. - композиция 2-х биективных функций, есть биективная функция. - отображение f: x
Бинарные отношения на множестве Х. Рефлексивность, симметричность, транзитивность бинарных отношений на множестве Х. n – арным отношениями между элементами множеств x1,x2,x3…..xn называется произвольное подмножество
Бинарным (двуместным) отношением между 2 множествами x и y, называется произвольное подмножество
Замечания: 1. Если x=y, то говорят, что
2. Множество х называется множеством области отправления, а y множеством области прибытия бинарного отношения. 3.Тот факт, что x Свойства: 1. Рефлексивонсть:
2. Симметричность:
3.Транзитивность:
x Отношение эквивалентности. Класс эквивалентности. Отношение рефлексивное, симметричное и транзитивное одновременное на множестве Х называется отношением эквивалентности. Классом эквивалентности порождённым элементом «х» называется подмножество множества Х, которое состоит из тех «у є х», которое состоит из «у є х» для которых «х ро у».
Двойственность. Закон двойственности. Пример. Замечание: будем рассматривать формулы, которые содержат только логические связки ͞, V, & Связки V, & назовем двойственными друг к другу. Формулы А и А˟ называются двойственными, если одна получена из другой одновременной заменой связок V, & на двойственную к ним.
Утверждение:
Закон двойственности Если формулы А и В равносильны, то и двойственные к ним А˟ и В˟ равносильны тоже. А=В => А*=В* Пример. А= (͞х1&х2& х3)V(х1 & ͞х2) V х3 А*= (͞х1Vх2V х3)&(х1 V ͞х2) & х3
Тождественно-истинные и тождественно-ложные формулы. Выполнимость и опровержимость формул. Пример. Правильные рассуждения. Пусть формула А зависит от списка переменных <х1, …, хn> Формула А называется тождественно-истинной (ложной), если на любых оценках списка переменных формула А принимает значение И (Л). Формула А называется выполнимой (опроверженной), если существует такая оценка списка переменных, на которой формула А принимает значение И(Л). 1)АV ͞А 2)А>A 3)A>(B>A) 4)A~A 5)((A>B)&A)>B 6)((A>B)& ͞B)> ͞A 7)((A>B)&(B>C))>(A>C) 8)(A>B)~(͞B > ͞A)
Отношение логического следования. Правильные рассуждения. Примеры. Пусть формулы А и В зависят от списка переменных <х1, …, хn>. Говорят, что формула В логически следует из формулы А тогда, когда их импликация – тождественная формула. А | = В <=>A>B = И Замечание: 1)Если В| = А, то говорят, что В выводима из А (А|- В), А\В) 2)Тождественно-истинная формула всегда выводима. Правильные рассуждения. В рассуждения, выводя одно высказывание из другого, мы пользовались законами логики. Тождественно истинные формулы логики высказываний выражают законы логики. Разумеется законы логики выражающиеся средствами логики высказываний не исчерпывают все законы логики использующиеся в рассуждениях. Законы логики высказываний могут служить основой лишь для тех выводов, в которых учитывается структура элементарных высказываний. Отвлекаясь от такого рассуждения, т.е. заменяя в нём элементарные высказывания высказывательными переменными мы получаем следующую схему вывода(умозаключения):
Формула ,причем различные значения n соответственно различные кортежи i(Ɛi1 … Ɛin) Формулы Любая булева функция представлена СДНФ т.е. виде f(х1, х2 … хn) = V (x1Ɛi & x2Ɛi &… & xnƐi) <Ɛi1, Ɛi2 …Ɛin> F(Ɛi1, Ɛi2 …Ɛin) =1
Представление булевых функций формулой логики высказываний в СДНФ и в СКНФ. Примеры. Рассм кортеж из нулей и единиц <ε1,ε2,...,εn> Xiεi = xi, если εi=1; xi, если εi=0; Xiεi = 1 тогда и только тогда, когда Xi = εi; Теорема(о разложении булевой ф-ции): каждая булева функция f(x1,x2,...,xn) (n≥1), не равная тождественно нулю может быть представлена в виде: f(x1,x2,...,xn)=∨i=12^n(&j=1nXεij&f(εi1, εi2,..., εin)) причем различным значениям i соответствуют различные кортежи < εi1, εi2,...,εin)) Следствие: любая булева функция представима в СДНФ, т.е. в виде f(x1,x2,...xn)= ∨(Xεi11& Xεi22&... Xεinn), где <εi1,εi2,...,εin> - оценка <f(εi1,εi2,...,εin)> - значение оценки Замечание: Аналогично доказывается теорема о представлении булевой функции в виде: &i=12^n(∨j=1nxj1-εij∨f(εi1,εi2,...,εin)) следствием из которой является формула &(x11-εi1∨x21-εi2∨...xn1-εin), где <εi1,εi2,...,εin> f(εi1,εi2,...,εin) =0 Рассм пример булевой функции и найдем СДНФ и СКНФ Для СДНФ - выделяем участки списка, где функция приняла значение 1 f(x1,x2)=(x1&x2)∨(x1&x2)∨(x1&x2) - СДНФ
Для СКНФ - берем оценку и вычитаем из единиц 11-10=01, возводим в степень оценки(более подробно см семинар 8-ое задан
f(x1,x2)=x1∨x2 - СКНФ К слову f(x1,x2)=x1⊃x2
Полные системы булевых функций. Теорема о сведении полноты одной системы булевых функцийк другой. Примеры полных систем. О: Система булевых функций {f1,f2,...,fm} из множества всех булевых функций называется полной, если любая булева функция может быть выражена через функции с помощью суперпозиций (подстановки функций в функцию)
k0={f1(x1,....,xn),f2(x1,...,xn),....,fm(x1,...xn)}
Функция f называется суперпозицией ранга 1(элементарной суперпозиций) функции f1,...,fm, если f может быть получено одним из след. способов: 1) из какой нибудь функции fi, переименованием переменной xj. f(x1,x2,...,xj,...xn) 2) подстановкой некоторой функции fl, где l=1,2,...,n вместо какого нибудь аргумента xj, взятого из множества k0 f(x1,x2,...,fl(x1,...,xn),...xn) Суперпозиция ранга 1 образует класс функций k1. Суперпозиция ранга r образует класс функций kr. Класс kr строится с помощью элементарных суперпозиций над классом kr-1 Суперпозициями функциями из k0 называются функции входящие в один из классов k0,k1,k2,...,kr. Теорема: Пусть даны 2 системы булевых функций: 1) F={f1,f2,...fm) ① 2) G={g1,g2,...,gl) ② относительно которых известно, что 1ая система полна и каждая её функция fi выражается через функции системы ② в виде формулы, тогда и вторая система полна. z=z(f1,f2,...,fm)=z(f1(g1,...,gl),...fm(g1,....,gl))=R(g1,...,gl) Примеры 1. {,&} - испытуемая ② {,∨,&} - ① Выразим x1∨x2=(x1∨x2)=(x1&x2)
2. {, ∨} ② x1&x2=(x1&x2)=(x1∨x2) {∨,&} - не выйдет
3. {|} - ② {,&} - ① x=x|x x1&x2=(x1|x2)|(x1|x2)
30. Полнота системы {+, ∙, 1}. Многочлены Жегалкины. Приведение любой булевой функции к многочлену жегалкина. {+, ∙, 1}, где ∙=& О: Булевы функции записанные в этой системе в виде многочлена называются многочленами Жегалкина. Приведение произвольной булевой функции к многочлену Жегалкина производится на основе правил обычной алгебры: 1) Законы коммутативности x1+x2=x2+x1; x1∙x2=x2∙x1; 2) Законы асоциативности x1+(x2+x3)=(x1+x2)+x3 x1(x2∙x3)=(x1∙x2)x3 3) x1(x2+x3)=x1x2+x1x3 - закон дистрибутивности 4) 0+х=х 5) 0∙х=0 6) 1∙х=х - действие с единицей и двух специальных правил: 7) х+х=0 8) х∙х=х СПОСОБЫ ПРЕДСТАВЛЕНИЯ БУЛЕВЫХ ФУНКЦИЙ МНОГОЧЛЕНАМИ ЖЕГАЛКИНА. 1 способ 1. Преобразуем булеву функцию в булеву функцию заданную в системе {,&} 2. Заменяем х=х+1, &=∙ 3. Применяем 8 правил алгебры Жегалкина, находим его многочлен.
2 способ 1. Находим СДНФ 2. Заменяем дизъюнкцию на f=∑⊕(x1εi1∙....∙xnεin)=Fi+Φi^ 3. Применяем 8 правил и находим многочлен Жегалкина Пример 1-ого способа: x1∨x2=(x1∨x2)=(x1&x2)=(x1+1)(x2+1)+1=x1x2+x2+x1+1+1=x1x2+x1+x2. Пример 2-ого способа: х1∨х2=(x1&x2)∨(x1&x2)∨(x1&x2)=(x1&x2)+(x1&x2)+(x1&x2)=(x1+1)x2+x1(x2+1)+x1x2=x1x2+x2+x1x2+x1+x1x2=x1x2+x2+x1
Ориентированные и неориентированные графы. Основные понятия. ОРИЕНТИРОВАННЫЕ ГРАФЫ.(ОРГРАФЫ) Пусть Х не пустое множество, а Х2=Х×Х - множество всех его пар. О: Пара <Г,Х>=G называется ориентированным графом (орграфом), где Г-произвольное подмножество множества Х2 (Г⊆Х2) Элементы х∈Х называются вершинами, а пара <X,Y>∈Г дугами орграфа. Замечание: тройку множеств <Г,Х,Y>, где Г⊆Х,Y называют многозначным отображателем из множества Х во множестве У. Обозначают Г:Х+Y. При этом, если х∈Х, то множество Г(х)={y∈Y|<x,y>∈Г}⊆Y называют образом элемента х, а Г-1(y)={x∈X|<x,y>∈Г}⊆X называют прообразом y. Если А⊆Х, то Г(А)=∨х∈АГ(х) - это образ множества А А⊆Y, то Г-1(А)=∨y∈AГ-1(А) - это прообраз мн-ва А Пусть задан орграф G=<Г,Х> 1. если y∈Г(х), т.е. <x,y> дуга, то говорят что она исходит из вершины х и заходит в у. 2. Дуга называется инцидентной в вершине х, если она заходит в х или исходит из х. 3. Дуга <x,х> называется петлей. 4. Вершина, не имеющая инцидентных дуг называется изолированной. Две вершины называются смежными, если существует дуга инцидентная им обоим. Пути в орграфе. О1: Последовательность дуг орграфа такая что начало каждой последующей дуги совпадает с концом предыдущей называется путем. О2: Путь у которого начало первой дуги совпадает с концом последней называется замкнутым путем, или контуром. О3: Путь (контур) называется элементарным, если все его вершины различны за исключением первой и последней. О4:Путь (контур) называется простым, если все его дуги различны. Примеры: 1) <x1,x2> <x2,x5> <x5,x4> - не контур, но простой эл-ый путь. 2) <x1,x2> <x2,x3> <x3,x1> - эл-ый простой путь, контур. 3) <x1,x2> <x2,x5> <x5,x4> <x4,x2> <x2,x3> <x3,x1> - контур, простой, не эл-ый 4) <x1,x2> <x2,x3> <x3,x1> <x1,x2> <x2,x3> <x3,x1> - не простой, не эл-ый, контур 5) <x1,x2> <x2,x5> <x5,x4> <x4,x2> <x2,x3> - не путь НЕОРИЕНТИРОВАННЫЕ ГРАФЫ Пусть Х-непустое множество. Х(2) - мн-во всех 2-х элементарных подмножеств множества Х. Пример: Х={1,2,3}. X(2)={{1,2},{1,3},{2,3}} О: Пара <Q,X>=G, где Q произвольное подмножество множества Х (Q⊆X) называется неориентированным графом. Элементы х∈Х - вершинами, а элементы {x,y}∈Q - (неупорядоченные пары) - ребрами. Замечание: неориентированные графы можно изучать как графы симметричных бинарных отношений. Подграфом графа G называется G’, если X’⊂X, Q’⊂Q (Г’⊂Г), а в случае если X’=X, то подграфом называют частичным графом. О1: Цепью неориентированного графа называется последотельность ребер, которая может быть перемещена в путь введением соответствующей ориентации на её ребрах. О2: Циклом называется цепь у которой 1-ая вершина совпадает с последней. О3: Цепь (цикл) называется элементарной, если некоторая вершина встречается в ней не более одного раза.
О4: Цепь (цикл) называется простой, если некоторой ребро встречается в ней не более одного раза.
37.Матричное задание графа. Матрицы сложности и инциденций. Цикломатическая матрица. G=<Г,х>, |x|=n, x={
Пример:
Для вершины
Замечание: для неориентированных графов матрица смежностей является симметричными, а элементы определиться следующим образом: 1 – существует ребро. 0 – в остальных случаях. Степень – число инцыдентных вершине рёбер. Матрица инциденций: G=<Г,х>, |x|=n, |Г|=N, x={ Пусть граф не имеет петель.
Замечание: для неориентированного графа инциденты определяются следующим образом:
Цикломатическая матрица: G=<Q,x> - неор. граф. n- вершины, N – ребра.
Алгоритм Форда Помечаем вершину xi индексом λi; Полагаем a=x6 и присваиваем ей λ6, причем λ0=0, а все остальные вершины помечаем λj=∞. Помечаем <xi,xj> для которой λi- λj˃l(xi,xj), затем заменяем индекс λj на индекс λ/J; λ/J= λi+ l(xi,xj)< λj Продолжаем процесс до тех пор пока не перестанут уменьшаться индексы. Предположим что алгоритм Форда выполним, тогда λn= λρ0. Среди дуг будет та по которой алгоритм Форда применим: λn- λρ1= l(x ρ1, xn) λ ρ1- λρ2= l(x ρ1, x ρ1) ………………… λ ρk- λ0= l(x 0, x ρk) ________________ (сложим все эти равенства) λ n= l(x 0, x ρk…………. x n). Возьмем x 0, x k1…………. x n предположим что он короче чем тот который мы нашли по алгоритму Форда: Λ0, λк1……………………………………………. λкn, -индексы присвоены по алгоритму Форда, где выполняется: Λk1- λ0≤ l(x 0, xr1) λ k2- λk1≤ l(x k1, x k2) ………………… λ n- λks≤ l(x ks, x n) ________________ (сложим все эти равенства) λ n≤l(x 0, x k…………. x n). значит метод Форда минимальный путь. Алгоритм Форда-Беллмана. Замечание: он позволяет по таблице значений λ(к)i (i=1…..n), (k=0,1……..n-1) и матрицы длин дуг λ(к)i= Замечание: к=0,1…………….n-1, λ1(к)=0; λ(0)i=∞, i=2,3…….n. Матрицу весов С опишем следующим образом Cij= алгоритм Форда-беллмана это модифицированный алгоритм Форда для матрицы весов дуг С, который может быть записан в виде: λ(к+1)j= Цикломатическая (контурная) матрица и матрица инциденций. Законы Киргофа. Уравнение контурных токов. Примеры. Матрица инциденций. Пусть задан граф G имеет N дуг и ребер и не имеет петель: G=<Г, х>; │х│=n; (-1 -если j дуга инцидентная i и вершина заходит в нее. Sij= (1 -если j дуга инцидентная i и вершина исходит из нее. (0 -если j дуга не Замечание: для неориентированного графа Sij определяется:
Sij =
Цикломатическая матрица. G=<Q, х>;(n- вершины; N-ребра) граф в котором μ1, μ2,……………………,μк – простые элемент циклы графа. Преобразуем неориентированный граф в ориентированный
в - матрица инциденций.
Законы Киргофа 1 закон - SI=0; S= [I1…………IN}]T 2 закон- BU=0; B=[U1…………UN}]T Уравнение контурных токов.- метод сокращения размерности системы уравнений, описывающей электрическую цепь. Как известно, любая электрическая цепь, состоящая из Р рёбер (ветвей, участков) и У узлов, может быть описана системой уравнений в соответствии с 1-м и 2-м законами Кирхгофа. Число уравнений в такой системе равно Р, из них У–1 уравнений составляется по 1-му закону Кирхгофа для всех узлов, кроме одного; а остальные Р–У+1 уравнений – по 2-му закону Кирхгофа для всех независимых контуров. Поскольку независимыми переменными в цепи считаются токи рёбер, число независимых переменных равно числу уравнений, и система разрешима. Существует несколько методов сократить число уравнений в системе. Одним из таких методов является метод контурных токов. Метод использует тот факт, что не все токи в рёбрах цепи являются независимыми. Наличие в системе У–1 уравнений для узлов означает, что зависимы У–1 токов. Если выделить в цепи Р–У+1 независимых токов, то систему можно сократить до Р–У+1 уравнений. Метод контурных токов основан на очень простом и удобном способе выделения в цепи Р–У+1 независимых токов. Метод контурных токов основан на допущении, что в каждом из Р–У+1 независимых контуров схемы циркулирует некоторый виртуальный контурный ток. Если некоторое ребро принадлежит только одному контуру, реальный ток в нём равен контурному. Если же ребро принадлежит нескольким контурам, ток в нём равен сумме соответствующих контурных токов (с учётом направления обхода контуров). Поскольку независимые контура покрывают собой всю схему (т.е. любое ребро принадлежит хотя бы одному контуру), то ток в любом ребре можно выразить через контурные токи, и контурные токи составляют полную систему токов.
Прямое произведение множеств. Отношения, бинарные отношения. Операции над отношениями. Прямым произведением множеств X u Y называется множество, состоящее из всех тех и только тех пар, первая компонента которой X*Y Пример: X = {a,b} Y = {1,2,3} X*Y={<a,1>,<a,2>,<a,3>,<b,1>,<b,2>,<b,3>} X*Y (*) X1,X2,…Xn Прямым произведением множества (*) называется множество, состоящее из всех тех и только тех картежей длины l, первая компонента которой Отношения, бинарные отношения. Рассмотрим вспомогательное понятие картеж. Упорядоченная пара <x,y> интуитивно определяется, как совокупность, состоящая из 2-х элементов х Две пары <x,y> u <U,V> равны тогда и только тогда, когда x=U, y=V <1,z> Картеж или упорядоченный набор n элементов x1 Два картежа
x2=y2 Число n – называется длинной картежа, а элементы xi – итой проэкцией (координата компоненты картежа). Операции над отношениями. 1. Для бинарных отношений обычным образом определены все теоретико-множественные операции: 2. Обратное отношение: обратным (инверсным) отношением называется отношение
3. Композиция отношений: а)
Композицией двух бинарных отношений
б) Композиция отношений на множестве X:
Замечание: Композиция отношений на множестве X порождает понятие: степень отношения
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 341; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.235.190 (0.014 с.) |

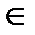 Х, а вторая Y.
Х, а вторая Y.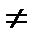 Y*X
Y*X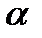 и
и 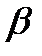 :
: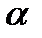 =<x1,x2…..xn>
=<x1,x2…..xn>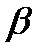 =<y1,y2….ym> равны тогда и только тогда, когда n = m и (x1=y1
=<y1,y2….ym> равны тогда и только тогда, когда n = m и (x1=y1  ,
,  ,\,
,\,  ,+,*
,+,*
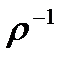 ={<x,y>| <y,x>
={<x,y>| <y,x> 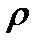 }
}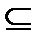 X*Y, которая определяется следующим образом:
X*Y, которая определяется следующим образом:
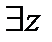
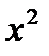
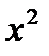
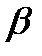
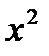
 y=z.
y=z. Y
Y х1,х2, y из того, что y=f(x1), y=f(x2)
х1,х2, y из того, что y=f(x1), y=f(x2) 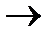 y, то говорят, что f – осуществляет взаимное однозначное соответствие, между множествами X и Y, а f: x
y, то говорят, что f – осуществляет взаимное однозначное соответствие, между множествами X и Y, а f: x 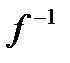 : y
: y 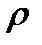 их прямого произведения x1*x2*…..*xn
их прямого произведения x1*x2*…..*xn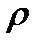
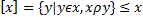
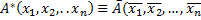 )
)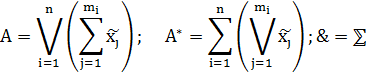
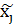 – высказывательная переменная (или отрицание высказ. Переменной)
– высказывательная переменная (или отрицание высказ. Переменной)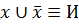
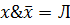
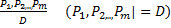





 её полустепенью захода называется число
её полустепенью захода называется число  , заходящих в неё дуг, а число
, заходящих в неё дуг, а число  полустепенью исхода исходящих дуг.
полустепенью исхода исходящих дуг. – называется степенью вершины.
– называется степенью вершины.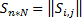


 - простые элементарные циклы, преобразуем в орграф:
- простые элементарные циклы, преобразуем в орграф: 


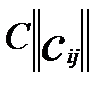 нагруженного орграфа определить минимальный путь из вершины а в любую достижимую вершину, причем из всех возможных путей он выделяет путь с наименьшим числом дуг.
нагруженного орграфа определить минимальный путь из вершины а в любую достижимую вершину, причем из всех возможных путей он выделяет путь с наименьшим числом дуг.
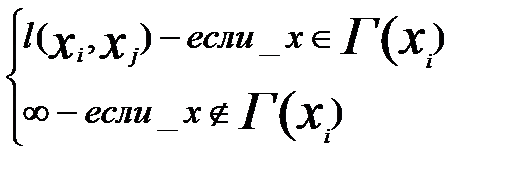
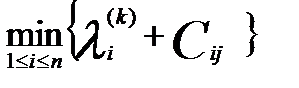
 =││Sij││;
=││Sij││; задав произвольную ориентацию на его ребрах, введем матрицу
задав произвольную ориентацию на его ребрах, введем матрицу  .Элементы матрицы:
.Элементы матрицы:  Примеры.
Примеры.



