Предикаты. Кванторы. Язык логики предикатов. Формулы логики предикатов. Равносильность и общезначимость формул логики предикатов. Основные равносильности.

ПРЕДИКАТЫ

Предложения типа «x больше z», «x+y=z», «x параллельно y» называются высказывательными формами и используются для задания предикатов.

О: Предикатом назовем n-местную функцию из некоторого множества M в множестве истиностнх значений {Л,И}, т.е. функцию вида: P(x1,x2,...,xn):M->{Л,И}

Предикатом от n переменных называют n-местным предикатом. Высказывание можно считать нуль местным предиктом.

Т.к. предикаты принимают только {Л,И}, то к ним применимы все логические операции.

Областью истинности предиката назовем мн-во всех элементов вида <a1,a2,...,an>∈Mn таких что P(a1,a2,...,an) - истинное высказывание.

КВАНТОРЫ

В логике высказываний кроме операций логики высказываний употребляют еще две операции.

1. Квантор общности ∀

Пусть P(x) одноместный предикат, тогда под выражением ∀xP(x) будем понимать: высказывание истинно тогда и только тогда, когда P(x) истинно для каждого x∈M. Это высказывание уже не зависит от x, а символ ∀x называют квантором общности.

2. Квантор существования ∃

Пусть P(x) одноместный предикат, тогда под выражением ∃xP(x) будем понимать высказывание истинное тогда и только тогда когда P(x) истинно хотя бы при одном x∈M

∃xP(x) читается - существует x для которого P(x). Также не зависит от x.

Замечание: Применение квантором P(x) называется связывание квантором.

Замечание2: Вместо слова «всякий» употребляют слова - «каждый», «всякий», а вместо «существует» употребляют слова - «есть», «найдется», «некоторые», «хотя бы один»

Следует обратить внимание на специфику употребления слова «некоторый». В обиходе имеется в виду - «по меньшей мере один, но не все». А в логике слово «некоторый» означает - «по меньшей мере 1, но может и все»

Замечение 3: Если множество M значения переменных является конечным, например M={a1,a2,...,an}, то

1)высказывание ∀xΦ(x) имеет тот же смысл, что и высказывания Φ(a1)&Φ(a2)&...&Φ(an)

2) высказывание ∃xΦ(x) имеет тот же смысл, что и высказывания Φ(a1)∨Φ(a2)∨... ∨Φ(an)

АЛФАВИТ ЛОГИКИ ПРЕДИКАТОВ

G=G1∨G2∨G3∨G4∨G5

1) G1={x1,x2,...xn} - предметные переменные.

2) G2={&,∨,⊃,∼} - логические связки.

3) G3={ (,) } - вспомогательные символ

4) G4={P1,P2,...Pi,...} - символы предикатов

5) G5={∀, ∃} - символы кванторов.

ФОРМУЛЫ ЛОГИКИ ПРЕДИКАТОВ

Слово логики высказываний(посмотрите может тут должно быть логики предикатов, но у меня почему-то так написанно) называется формулой, если оно удовлетворяет следующему определению:

1) Если P символ предиката, x1,x2,...,xn символы предметных переменых, необязательно различные, то P(x1,x2,...xk) - атомарная формула. Все предметные переменные атомарной формулы свободны, связаных переменных нет.

2) Пусть A - формула, тогда «неверно что A» также формула, т.е. А - тоже формула. Свободные и связные переменные формулы А это свободные и связные переменные формулы А.

3) Пусть А и В формулы, тогда (А∨В), (А&В), (А⊃В), (А∼В) - формулы, если в А и В нет таких предметных переменных, которые связанны в одной и свободны в другой.

4) Если А формула, а x предметная переменная, тогда ∀xA(x),∃xA(x) - формулы(в этом случае А называют областью действия квантора общности или сущ.)

5) Других формул, кроме пунктов 1-4 нет.

Замечание: вхождение переменной x в формулу называется связанным, если оно входит в область действия квантора общности или существования.

РАВНОСИЛЬНОСТИ И ПРАВИЛА РАВНОСИЛЬНЫХ ПРЕОБРАЗОВАНИЙ В ЛОГИКЕ ПРЕДИКАТОВ

Замечание: очевидно, что для формул логики предикатов сохраняются все равносильности и правила авносильных преоразований логики высказываний.

1. Перенос квантора через отрицание.

Пусть А формула содержащая свободную переменную X, тогда справедливо след. равносильности.

1) (∀xA(x))≡∃xA(x)

2) (∃xA(x))≡∀x(A(x))

Это обощение закона Де Моргана.

2. Вынос квантора за скобки.

Пусть формула А содержит свободную переменную х, а формула В не содержит, тогда справедлива след равносильности:

1) ∀xA(x)&B≡∀x(A(x)&B)

2) ∃xA(x)∨B≡∃x(A(x)∨B)

3) ∀xA(x)∨B≡∀x(A(x)∨B)

4) ∃xA(x)&B≡∃x(A(x)&B)

5) ∀xA(x)⊃B≡∃x(A(x)⊃B)

6) ∃xA(x)⊃B≡∀x(A(x)⊃B)

7) В⊃∀x(A(x)≡∀x(B⊃A(x))

8) B⊃∃xA(x)≡∃x(B⊃A(x))

Замечание:

1’) ∀xA(x)&∀xB(x)≡∀x(A(x)&B(x))

2’) ∃xA(x)∨∃xB(x)≡∃x(A(x)∨B(x))

3’) ∀xA(x)∨∀xB(x)≠∀x(A(x)∨B(x))

4’) ∃xA(x)&∃xB(x)≠∃x(A(x)&B(x))

3.Перестановка одноименных кванторов.

1) ∀x∀yA(x,y)≡∀y∀xA(x,y)

2) ∃x∃yA(x,y)≡∃y∃xA(x,y)

4.Переименование связанных переменных.

Заменяя связанную переменную заданную формулу другой переменной не входящей в эту формулу в кванторе и всюду в области действия квантора получим формулу равносильную данной

1) ∀xA(x)≡∀yA(y)

2) ∃xA(x)≡∃yA(y)

 

Понятие интерпретации. Равносильность и общезначимость формул логики предикатов. Приведенная нормальная формула логики предикатов. Проблема разрешимости. Формулировка теоремы Черча.

ИНТЕРПРЕТАЦИЯ

Формулы имеют смысл тогда и только тогда, когда заданна какая-нибудь интерпретация входящих в неё символов.

О: Под интерпретацией будем понимать: всякую систему, состоящую из некоторого множества М, названного областью интерпретации и какого-либо соответствия, относящего к каждому символу предиката Pi, определенный и местный предикат.

Замечание: при заданной интерпретации мы считаем, что предметные переменные пробегают множество М, символы, ∨, &, ⊃, ∼, ∀, ∃ имеют свой обычный смысл.

Для данной формулы интерпретации каждая формула без свободных переменных представляет собой высказывание, которое истинно или ложно. А всякая формула со свободными

переменными выражает некоторый предикат на обл интерпретации, который истинен на одних значениях предметных переменных из обл. интерпретации и ложен на других.

РАВНОСИЛЬНОСТЬ ФОРМУЛЫ ЛОГИКИ ВЫСКАЗЫВАНИЙ.

Рассм две формулы F и G, у них одно и тоже мн-во свободных переменых.

О1: Формулы F и G равносильны данной интерпретации, если на любом наборе значений свободных переменных они принимают одинаковые истиностные значения(т.е. если формулы выражают в данной интерпретации один и тот же предикат).

О2: Формулы F и G равносильны на множестве M, если они равносильны во всех интерпретациях, заданных на множестве М.

О3: Формулы F и G равносильны (в логике предикатов), если они равносильны во всех множествах.

Обозначение: F≡G

ОБЩЕЗНАЧИМОСТЬ. ВЫПОЛНИМОСТЬ.

Рассм некоторую интерпретацию с областью М.

О1: Говорят, что формула А выполнима в данной интерпретации, если существует набор <a1,a2,...an>, где ai∈M, значений свободных переменных Xk1,Xk2,...,Xkn формула А таких что A|<a1,...,an>=И на этом наборе.

О2: Говорят, что формула А истина в данной интерпретации, если она принимает значение i на любом наборе <a1,a2,...an> значений свободных переменных Xk1,Xk2,...,Xkn

О3: Говорят, что формула А общезначима или тождественно-истинна(в логике предикатов), если она истинна в каждой интерпретации.

О4: Говорят, что формула А выполнима(в логике предикатов), если существует интерпретация в которой она выполнима.

Примеры общезначимых формул:

1) тождественно-истинные формула логики высказываний.

2) ∀xA(x)⊃A(y)

3) A(x)⊃∃yA(y)

Для доказательства, что формула истинна используется второй способ из девятого задания курсовой.

РАЗРЕШИМОСТЬ

Замечание: задача распознавания общезначимых формул логики предикатов существенно сложнее, чем для логики высказываний. Она носит название проблемы разрешимости. В логике высказываний эта проблема была решена. В логике предикатов эта проблема не разрешима.

Т.Черча: Не существует алгоритма, который для любой формулы логики предикатов устанавливал общезначима она или нет.

Замечание: Однако эта проблема разрешима в логике одноместных предикатов(в логике, созданной Аристотелем).

ПРИВЕДЕННЫЕ ФОРМУЛЫ.

О: Формулы в которых из логических символов встречается, ∨, &, а символ встречается только перед символом атамарного предиката называется приведенной.

Примеры приведенных формул:

1) А(x1,x2)∨A(x1,x3)

2) ∀хA(x,y)∨∃xA(x,y)

3) (A(x,y)⊃B(x,y)) - не может быть приведенной.

Т1: Для любой формулы существует равносильная ей приведенная формула. Причем множество свободных и связанных переменных совпадает.

О: Приведенная формула называется нормальной, если она не содержит символов кванторов или все символы кванторов стоят впереди.

Т2: Для любой приведенной формулы существует равносильная ей нормальная формула.

Т3: Для любой формулы существует равносильная ей нормальная формула.

Ориентированные и неориентированные графы. Основные понятия.

ОРИЕНТИРОВАННЫЕ ГРАФЫ.(ОРГРАФЫ)

Пусть Х не пустое множество, а Х2=Х×Х - множество всех его пар.

О: Пара <Г,Х>=G называется ориентированным графом (орграфом), где Г-произвольное подмножество множества Х2 (Г⊆Х2)

Элементы х∈Х называются вершинами, а пара <X,Y>∈Г дугами орграфа.

Замечание: тройку множеств <Г,Х,Y>, где Г⊆Х,Y называют многозначным отображателем из множества Х во множестве У. Обозначают Г:Х+Y.

При этом, если х∈Х, то множество Г(х)={y∈Y|<x,y>∈Г}⊆Y называют образом элемента х, а Г-1(y)={x∈X|<x,y>∈Г}⊆X называют прообразом y.

Если А⊆Х, то Г(А)=∨х∈АГ(х) - это образ множества А

А⊆Y, то Г-1(А)=∨y∈AГ-1(А) - это прообраз мн-ва А

Пусть задан орграф G=<Г,Х>

1. если y∈Г(х), т.е. <x,y> дуга, то говорят что она исходит из вершины х и заходит в у.

2. Дуга называется инцидентной в вершине х, если она заходит в х или исходит из х.

3. Дуга <x,х> называется петлей.

4. Вершина, не имеющая инцидентных дуг называется изолированной. Две вершины называются смежными, если существует дуга инцидентная им обоим.

Пути в орграфе.

О1: Последовательность дуг орграфа такая что начало каждой последующей дуги совпадает с концом предыдущей называется путем.

О2: Путь у которого начало первой дуги совпадает с концом последней называется замкнутым путем, или контуром.

О3: Путь (контур) называется элементарным, если все его вершины различны за исключением первой и последней.

О4:Путь (контур) называется простым, если все его дуги различны.

Примеры:

1) <x1,x2> <x2,x5> <x5,x4> - не контур, но простой эл-ый путь.

2) <x1,x2> <x2,x3> <x3,x1> - эл-ый простой путь, контур.

3) <x1,x2> <x2,x5> <x5,x4> <x4,x2> <x2,x3> <x3,x1> - контур, простой, не эл-ый

4) <x1,x2> <x2,x3> <x3,x1> <x1,x2> <x2,x3> <x3,x1> - не простой, не эл-ый, контур

5) <x1,x2> <x2,x5> <x5,x4> <x4,x2> <x2,x3> - не путь

НЕОРИЕНТИРОВАННЫЕ ГРАФЫ

Пусть Х-непустое множество. Х(2) - мн-во всех 2-х элементарных подмножеств множества Х.

Пример: Х={1,2,3}. X(2)={{1,2},{1,3},{2,3}}

О: Пара <Q,X>=G, где Q произвольное подмножество множества Х (Q⊆X) называется неориентированным графом. Элементы х∈Х - вершинами, а элементы {x,y}∈Q - (неупорядоченные пары) - ребрами.

Замечание: неориентированные графы можно изучать как графы симметричных бинарных отношений.

Подграфом графа G называется G’, если X’⊂X, Q’⊂Q (Г’⊂Г), а в случае если X’=X, то подграфом называют частичным графом.

О1: Цепью неориентированного графа называется последотельность ребер, которая может быть перемещена в путь введением соответствующей ориентации на её ребрах.

О2: Циклом называется цепь у которой 1-ая вершина совпадает с последней.

О3: Цепь (цикл) называется элементарной, если некоторая вершина встречается в ней не более одного раза.

О4: Цепь (цикл) называется простой, если некоторой ребро встречается в ней не более одного раза.

 

37.Матричное задание графа. Матрицы сложности и инциденций. Цикломатическая матрица.

G=<Г,х>, |x|=n, x={

Пример:

 

Для вершины её полустепенью захода называется число , заходящих в неё дуг, а число полустепенью исхода исходящих дуг.

– называется степенью вершины.

Замечание: для неориентированных графов матрица смежностей является симметричными, а элементы определиться следующим образом:

1 – существует ребро.

0 – в остальных случаях.

Степень – число инцыдентных вершине рёбер.

Матрица инциденций:

G=<Г,х>, |x|=n, |Г|=N, x={

Пусть граф не имеет петель.

Замечание: для неориентированного графа инциденты определяются следующим образом:

Цикломатическая матрица:

G=<Q,x> - неор. граф.

n- вершины, N – ребра.

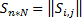
- простые элементарные циклы, преобразуем в орграф: