
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вектор-циклы. Пространство вектор циклов. Независимые циклы. Цикломатическое число. Алгоритм нахождения базис вектор-циклов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
О: вектор С(μ)∈Zn – называется вектор-циклом соответствующим циклу μ если i- координаты Сi(μ) вектора С(μ) равны разности Сi+(μ) - Сi-(μ) где Сi+ - число проходов в цикле μ через ребро qi в направлении выбранной ориентации, Сi- - число проходов в цикле μ через ребро qi в противоположном направлении выбранной ориентации.
С(μ)-соответствуют циклу μ выражается в виде линейной комбинации через другие вектора циклы. С(μ)=α1 С(μ1)+ α2С(μ2)+ ……………………+ αmС(μm) (1) Где α1 ∈Q (множество рациональных чисел) Коэффициент αi коэффициент линейного разложения вектор цикла С(μ) по вектор-циклам С(μ1)……………………+ С(μm) Теорема1: Если при некоторых α1…………………… αm справедливо равенство (1) для некоторой выбранной ориентации ребер то равенство (1) остается справедливы и при любой другой ориентации. О: цикл μ называется суммой циклов μ1 и μ2 при этом μ= μ1 + μ2 если их вектор-циклы удовлетворяют условию: С(μ)=С(μ1)+ С(μ2) О: о двух циклах μ1и μ2 говорят что μ1= αμ2 если С(μ1)= αС(μ2) О: цикл μ называется линейной комбинацией циклов μ1, μ2 и т д если цикл С(μ)=α1 С(μ1)+ α2С(μ2)+ ……………………+ αmС(μm) при этом μ=α1 μ1+ α2μ2+ ……………………+ αmμm (4) О: система циклов μ1, μ2…… и т д, называется линейно независимой из равенства α1 μ1+ α2μ2+ ……………………+ αmμm =0 следует равенство 0 всех коэффициентов α О: система независимых циклов называется цикловым базисом графа G если любой цикл из G может быть представлен в виде линейной комбинации из элементов базиса. Теорема2: в любом графе G существует цикловой базис состоящий из простых элементарных циклов этого графа. О: цикломатическим числом графа G называется число элементов его циклового базиса (максимальное число независимых циклов) Алгоритм нахождения базис вектор-циклов G=<Q, X> │Q│= N. T- остовное дерево G (графа); q1……………..qm – ребра Т; qn…………..qm – остальные ребра графа G, возьмем qi, i=n, n+1, ……N; и добавим это ребро в дерево Т пусть qi={x,y} дерево имеет две вершины x…..y назовем μi*(n-1); { μ1,….. μN-n+1}- линейно независимый образующий базис. Связь базиса вектор-циклов с цикломатической матрицей.
Цикломатическая (контурная) матрица и матрица инциденций. Законы Киргофа. Уравнение контурных токов. Примеры. Матрица инциденций. Пусть задан граф G имеет N дуг и ребер и не имеет петель: G=<Г, х>; │х│=n; (-1 -если j дуга инцидентная i и вершина заходит в нее. Sij= (1 -если j дуга инцидентная i и вершина исходит из нее. (0 -если j дуга не Замечание: для неориентированного графа Sij определяется:
Sij =
Цикломатическая матрица. G=<Q, х>;(n- вершины; N-ребра) граф в котором μ1, μ2,……………………,μк – простые элемент циклы графа. Преобразуем неориентированный граф в ориентированный
в - матрица инциденций.
Законы Киргофа 1 закон - SI=0; S= [I1…………IN}]T 2 закон- BU=0; B=[U1…………UN}]T Уравнение контурных токов.- метод сокращения размерности системы уравнений, описывающей электрическую цепь. Как известно, любая электрическая цепь, состоящая из Р рёбер (ветвей, участков) и У узлов, может быть описана системой уравнений в соответствии с 1-м и 2-м законами Кирхгофа. Число уравнений в такой системе равно Р, из них У–1 уравнений составляется по 1-му закону Кирхгофа для всех узлов, кроме одного; а остальные Р–У+1 уравнений – по 2-му закону Кирхгофа для всех независимых контуров. Поскольку независимыми переменными в цепи считаются токи рёбер, число независимых переменных равно числу уравнений, и система разрешима. Существует несколько методов сократить число уравнений в системе. Одним из таких методов является метод контурных токов. Метод использует тот факт, что не все токи в рёбрах цепи являются независимыми. Наличие в системе У–1 уравнений для узлов означает, что зависимы У–1 токов. Если выделить в цепи Р–У+1 независимых токов, то систему можно сократить до Р–У+1 уравнений. Метод контурных токов основан на очень простом и удобном способе выделения в цепи Р–У+1 независимых токов. Метод контурных токов основан на допущении, что в каждом из Р–У+1 независимых контуров схемы циркулирует некоторый виртуальный контурный ток. Если некоторое ребро принадлежит только одному контуру, реальный ток в нём равен контурному. Если же ребро принадлежит нескольким контурам, ток в нём равен сумме соответствующих контурных токов (с учётом направления обхода контуров). Поскольку независимые контура покрывают собой всю схему (т.е. любое ребро принадлежит хотя бы одному контуру), то ток в любом ребре можно выразить через контурные токи, и контурные токи составляют полную систему токов.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.01 с.) |


 - множество всех векторов-циклов графа G.
- множество всех векторов-циклов графа G.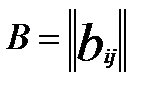


 =││Sij││;
=││Sij││; задав произвольную ориентацию на его ребрах, введем матрицу
задав произвольную ориентацию на его ребрах, введем матрицу  .Элементы матрицы:
.Элементы матрицы:  Примеры.
Примеры.



