
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение вектора по базису. Координатное представление.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Три линейно независимых вектора a, b и c образуют в пространстве базис, если любой вектор d может быть представлен в виде некоторой линейной комбинации векторов a, b и c, т. е. если для любого вектора d найдутся такие вещественные числа λ, μ и ν, что справедливо равенство: d = λ a + μ b + ν c. Два лежащих в плоскости π линейно независимых вектора a и b образуют на этой плоскости базис, если любой лежащий в плоскости π вектор c может быть представлен в виде некоторой линейной комбинации векторов a и b, т. е. если для любого лежащего в плоскости π вектора c найдутся такие вещественные числа λ, и μ, что справедливо равенство: c = λ a + μ b. Справедливы следующие фундаментальные утверждения: 1) любая тройка некомпланарных векторов a, b и c образует базис в пространстве; 2) любая пара лежащих в данной плоскости неколлинеарных векторов a и b образует базис на этой плоскости. Принято называть равенство d = λ a + μ b + ν c разложением вектора d пo базису a, b, c, а числа λ, μ и ν — координатами вектора d относительно базиса a, Ь, c. Аффинные координаты в пространстве определяются заданием базиса a, b, c и некоторой точки O, называемой началом координат. Аффинными координатами любой точки M называются координаты вектора OM (относительно базиса a, b, c). Так как каждый вектор OM может быть, и притом единственным способом, разложен по базису a, b, c, то каждой точке пространства M однозначно соответствует тройка аффинных координат λ, μ, ν.
Координаты вектора и точки в декартовой системе координат. Декартова прямоугольная система координат является частным случаем аффинной системы. В случае декартовой прямоугольной системы базисные векторы принято обозначать не буквами a, b, c, а буквами i, j, k. Итак, каждый из векторов i, j, k имеет длину, равную единице, причем эти три вектора взаимно-ортогональны (обычно направления векторов i, j, k берут совпадающими с направлениями декартовых осей Oх, Oy и Oz соответственно). Если скалярное произведение двух элементов пространства равно нулю, то они называются ортогональными друг другу. Каждый вектор d может быть разложен единственным способом по декартову прямоугольному базису i, j, k, т. е. для каждого вектора d найдется единственная тройка чисел X, Y и Z такая, что справедливо равенство: d = X i + Y j + Z k. Числа X, Y, Z называются декартовыми прямоугольными координатами вектора d. Если вектор d имеет декартовы прямоугольные координаты X, У, Z, то мы будем использовать следующую символику: d ={X, Y, Z}. Декартовы прямоугольные координаты X, Y и Z вектора d равны проекциям этого вектора на оси Oх, Oу и Oz соответственно. Возьмем произвольную точку М на прямой a. Декартовой координатой x точки M будем называть величину направленного отрезка Длина вектора. Расстояние между двумя точками. Орт вектора. Координаты орта. Косинусы направления. Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора. Для обозначения модуля вектора используются две вертикальные линии слева и справа | Величина М1М2 направленного отрезка М1М2 равна x2 — х1 т. е. М1М2 = х2-х1. Рассмотрим в пространстве декартову систему координат Oxyz и точки M1(x1,y1,z1) и М2{х2, у2, z2) Расстояние ρ(М1, М2) между точками М1 и М2, равное длине направленного отрезка Используя теорему Пифагора, получим следующую формулу для ρ(М1, М2): ρ(М1, М2) = Формула расстояния между двумя точками в случае их расположения в плоскости Оху имеет следующий вид: ρ(М1, М2) = Ортом произвольного ненулевого вектора c назовем единичный вектор, коллинеарный c и имеющий одинаковое с c направление. Координаты орта - координаты a0 ( Косинусы направления вектора - это косинусы углов, которые образует вектор с осями координат.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 708; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.42.247 (0.006 с.) |

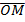 .
. |.
|.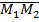 , равно также длине диагонали параллелепипеда, грани которого параллельны координатным плоскостям и проходят через точки М1 и М2. Длина параллельного оси Ох ребра этого параллелепипеда равна, абсолютной величине проекции отрезка М1М2 на ось Ох, т. е., согласно формуле равна |x1 —x2|. По аналогичным соображениям длины ребер, параллельных осям Оу и Oz, равны соответственно |y2 — y1| и |z2 — z1|.
, равно также длине диагонали параллелепипеда, грани которого параллельны координатным плоскостям и проходят через точки М1 и М2. Длина параллельного оси Ох ребра этого параллелепипеда равна, абсолютной величине проекции отрезка М1М2 на ось Ох, т. е., согласно формуле равна |x1 —x2|. По аналогичным соображениям длины ребер, параллельных осям Оу и Oz, равны соответственно |y2 — y1| и |z2 — z1|.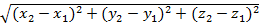
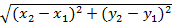
 ), где a0 орт вектор.
), где a0 орт вектор.


