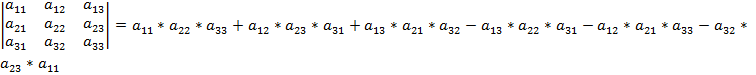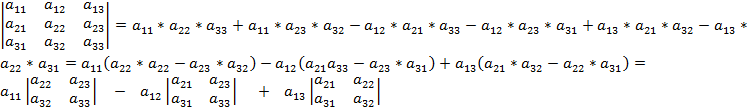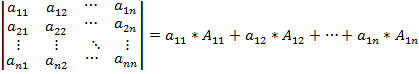Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители второго и третьего порядка и их вычисление. Определение определителя любого порядка. Алгебраические дополнения. Перечислить свойства определителя.Содержание книги
Поиск на нашем сайте
Определители второго и третьего порядка и их вычисление. Определение определителя любого порядка. Алгебраические дополнения. Перечислить свойства определителя. Определитель (детерминант) – число, которое ставится в соответствие квадратной таблице чисел по определенным правилам. Определитель второго порядка:
При транспонировании определитель не меняется. Определитель = 0, когда: или Определитель 3-го порядка -
или (минор 1 элемента) (минор 2 элемента) (минор 3 элемента) Если минор домножить на «-», то он становится алгебраическим дополнением. Aij=Mij*(-1)i+j Определитель n-ого порядка: Свойства: 1) При транспонировании определитель не меняется. 2) При перестановке любых 2 строк(столбцов) определитель меняет знак. 3) Если в определителе 2 строки (столбца) одинаковы, то определитель = 0. 4) Если какая либо строка или столбец состоит только из 0, то определитель = 0. 5) Если в определителе 2 строки или 2 столбца пропорциональны, то определитель = 0. 6) Число, умноженное на определитель = определителю у которого одна строка или столбец умножена на это число. 7) Пусть 2 определителя отличаются только 2 строками, тогда сумма определителя = определителю, у которого одинаковые строки остаются, а не одинаковые складываются. 8) Если какая то строка является линейной комбинацией остальных строк, то определитель = 0. 9) Если в какой-либо строке добавить линейную комбинацию каких-нибудь других строк, то определитель не меняется. 10) Определитель = сумме произведений элементов какой-либо одной строки на их алгебраическое дополнение. 11) Сумма произведений элементов какой-либо строки (или какого-либо столбца) определителя на соответствующие алгебраические дополнения элементов любой другой строки (любого другого столбца) равна нулю. 12) Определитель = 0, ó какая-либо строка является линейной комбинацией другой строки.
Будем говорить, что некоторая строка (а1, a2,..., аn) является линейной комбинацией строк (b1, b2,...,bn), (c1 c2,..., cn),.... (d1 d2,.... dn) с коэффициентами λ, μ,...,ν, если аj= λbj + μcj +... + νdj для всех j— 1, 2,.... n.
Определение вектора. Равенство векторов. Сумма векторов и ее свойства. Произведения векторов и числа и его свойства. Геометрическим вектором (или просто вектором) называется направленный отрезок.
Отрезок называется направленным, если указано, какая из ограничивающих его точек считается началом, какая – концом. Два вектора называются равными, если они коллинеарные, имеют одинаковую длину и одинаковое направление. Все нулевые векторы считаются равными. Вектор называется нулевым, если начало и конец его совпадают. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Из определения равенства векторов непосредственно вытекает следующее утверждение: каковы бы ни были вектор а и точка Р, существует, и притом единственный, вектор PQ с началом в точке Р, равный вектору а.
Суммой a + b двух векторов a и b называется вектор, идущий из начала вектора a в конец вектора b при условии, что вектор b приложен к концу вектора a. Правило сложения двух векторов, содержащееся в этом определении, обычно называют правилом треугольника. Свойства: 1) а + b = b + а (переместительное свойство); 2) (а + b) + с = а + (b + с) (сочетательное свойство); 3) Существует нулевой вектор 0 такой, что a + 0 = a для любого вектора a (особая роль нулевого вектора); 4) Для каждого вектора a существует противоположный ему вектор a ’ такой, что a + a ’ = 0.
Произведением α а (или а α) вектора a на вещественное число α называется вектор Ь, коллинеарный вектору а, имеющий длину, равную | а |*|α|, и имеющий направление, совпадающее с направлением вектора а в случае а > 0 и противоположное направлению вектора а в случае а < 0. Свойства: 1) α(a + b)= α a + α b (распределительное свойство числового сомножителя относительно суммы векторов); 2) (α + β) а = α а + β а (распределительное свойство векторного сомножителя относительно суммы чисел); 3) α(β а) = (αβ) a (сочетательное свойство числовых сомножителей).
Эти свойства имеют фундаментальное значение, ибо они позволяют производить выкладки в векторной алгебре по тем правилам, по которым производятся аналогичные выкладки в обычной алгебре.
Определители второго и третьего порядка и их вычисление. Определение определителя любого порядка. Алгебраические дополнения. Перечислить свойства определителя. Определитель (детерминант) – число, которое ставится в соответствие квадратной таблице чисел по определенным правилам.
Определитель второго порядка:
При транспонировании определитель не меняется. Определитель = 0, когда: или Определитель 3-го порядка -
или (минор 1 элемента) (минор 2 элемента) (минор 3 элемента) Если минор домножить на «-», то он становится алгебраическим дополнением. Aij=Mij*(-1)i+j Определитель n-ого порядка: Свойства: 1) При транспонировании определитель не меняется. 2) При перестановке любых 2 строк(столбцов) определитель меняет знак. 3) Если в определителе 2 строки (столбца) одинаковы, то определитель = 0. 4) Если какая либо строка или столбец состоит только из 0, то определитель = 0. 5) Если в определителе 2 строки или 2 столбца пропорциональны, то определитель = 0. 6) Число, умноженное на определитель = определителю у которого одна строка или столбец умножена на это число. 7) Пусть 2 определителя отличаются только 2 строками, тогда сумма определителя = определителю, у которого одинаковые строки остаются, а не одинаковые складываются. 8) Если какая то строка является линейной комбинацией остальных строк, то определитель = 0. 9) Если в какой-либо строке добавить линейную комбинацию каких-нибудь других строк, то определитель не меняется. 10) Определитель = сумме произведений элементов какой-либо одной строки на их алгебраическое дополнение. 11) Сумма произведений элементов какой-либо строки (или какого-либо столбца) определителя на соответствующие алгебраические дополнения элементов любой другой строки (любого другого столбца) равна нулю. 12) Определитель = 0, ó какая-либо строка является линейной комбинацией другой строки.
Будем говорить, что некоторая строка (а1, a2,..., аn) является линейной комбинацией строк (b1, b2,...,bn), (c1 c2,..., cn),.... (d1 d2,.... dn) с коэффициентами λ, μ,...,ν, если аj= λbj + μcj +... + νdj для всех j— 1, 2,.... n.
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 198; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.248.62 (0.009 с.) |

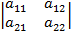 =
= 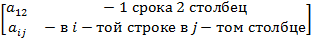 =
= 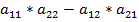
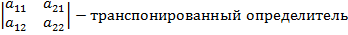
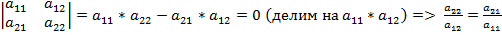
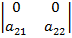 =0
=0