
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Классы Поста и замыкание. Полнота системы булевых функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Сколько функций содержит множество: а) г) 2. Доказать, что ни один из классов Поста не содержится в другом. 3. Пусть 4. Показать, что если 5. Доказать, что функция, двойственная монотонной функции, монотонна. 6. Доказать, что функция, двойственная линейной функции, линейна. 7. Доказать, что пересечение замкнутых классов – замкнутый класс. 8. Является ли объединение замкнутых классов замкнутым классом? 9. Доказать, что совокупность функций, двойственных функциям из функционально замкнутого класса, образует функционально замкнутый класс. 10. Назовем булеву функцию Замечание. Задача 10объясняет, почему в теории булевых функций не рассматривают монотонно невозрастающие функции. Дело в том, что интерес представляют свойства функций, которые «наследуются» при задании функций формулами, т.е. такие свойства, которые выделяют обладающие ими функции в замкнутый класс. Множество монотонно невозрастающих функций замкнутым не является. 11. Дана произвольная несамодвойственная функция. Отождествить у нее некоторые переменные так, чтобы получилась несамодвойственная функция от возможно меньшего числа переменных. 12. Дана произвольная немонотонная функция. Отождествить у нее некоторые переменные так, чтобы получилась немонотонная функция от возможно меньшего числа переменных. 13. Доказать, что для монотонных функций справедливо разложение 14. Показать, что 15. Найти число линейных функций от n переменных, существенно зависящих ровно от k переменных. 16. Используя теорему о полноте двух систем, доказать, что а) 17. Опираясь на доказательство леммы о функции, не сохраняющей 0, реализовать формулой над множеством 18. Опираясь на доказательство леммы о функции, не сохраняющей 1, реализовать формулой над множеством 19. Опираясь на доказательство леммы о несамодвойственной функции, реализовать формулой над множеством 20. Опираясь на доказательство леммы о немонотонной функции, реализовать формулой над множеством 21. Опираясь на доказательство леммы о нелинейной функции, реализовать формулой над множеством 22. Доказать, что из любой полной системы можно выделить полную подсистему, содержащую не более пяти функций. 23. Доказать, что всякий замкнутый класс функций, не совпадающий с 24. Назовем систему булевых функций предполным классом, если эта система неполна и добавление к ней любой функции, ей не принадлежащей, приводит к образованию полной системы. Доказать, что: а) классы Поста являются предполными; б) других предполных классов, кроме классов Поста, нет. 25. Доказать, что во всяком базисе содержится не более 4-х функций. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ Задание предоставляется индивидуально из учебного пособия Кожухов И. Б., Ревякин А. М., Бардушкина И. В. Дискретная математика: Учебное пособие для студентов специализации «Информационная безопасность». М.: Изд. центр МГАДА, 2013. — 366 с. Примерные вопросы к экзамену. 1. Введение в математическую логику. Высказывания, функции алгебры логики. Формулы. Реализация функций формулами. 2. Булевы векторы и булевы функции. Элементарные булевы функции. Задание булевых функций формулами. Основные равносильности. 3. Существенные и фиктивные переменные булевых функций. Операция удаления (введения) фиктивной переменной. 4. Двойственные функции. Принцип двойственности. 5. Разложение булевых функций по переменным. 6. Совершенная дизъюнктивная нормальная форма функции. 7. Совершенная конъюнктивная нормальная форма функции. 8. Постановка задачи о минимизации ДНФ. Минимальная ДНФ. Сокращенная ДНФ. Тупиковые ДНФ. 9. Алгоритм поиска сокращенных, тупиковых и минимальных ДНФ. 10. Представление функций в виде полинома Жегалкина (существование и единственность). Поиск полинома Жегалкина методом равносильных преобразований и методом неопределенных коэффициентов. 11. Класс функций, сохраняющих 0. Класс функций, сохраняющих 1. Класс самодвойственных функций. Класс монотонных функций. Класс линейных функций 12. Замыкание системы булевых функций. Свойства замыкания. Теорема о замкнутости классов Поста. 13. Полные системы булевых функций. Теорема о полноте двух систем. Примеры полных систем. Базисы. 14. Лемма о функции, не сохраняющей 0. Лемма о функции, не сохраняющей 1. 15. Лемма о несамодвойственной функции. 16. Лемма о немонотонной функции. 17. Лемма о нелинейной функции. 18. Критерий полноты системы булевых функций (теорема Поста Эквивалентность формул. Свойства элементарных функций. Принцип двойственности. 19. Разложение булевых функций по переменным. Совершенная дизъюнктивная нормальная форма. 20. Полнота и замкнутость. 21. Важнейшие замкнутые классы. Теорема о полноте. 22. Алгоритмы построения минимальных дизъюнктивных нормальных форм для функций алгебры логики. 23. Основные понятия теории дизъюнктивных нормальных форм. 24. Допустимые конъюнкции. Сокращенная ДНФ. 25. Тупиковые ДНФ. Алгоритм построения всех тупиковых ДНФ. 26. Логика предикатов. Основные определения. 27. Формулы логики предикатов. 28. Утверждения и их отрицания. 29. Полнота, замкнутость. Теорема Поста о полноте. 30. Схемы из функциональных элементов. 31. Функции 32. О понятии алгоритма. Тезис Чёрча. 33. Машина Тьюринга. 34. Рекурсивные функции. 35. Операторы суперпозиции и примитивной рекурсии. Примитивно рекурсивные функции. 36. Оператор минимизации. Рекурсивные функции. 37. Разрешимые и перечислимые множества. Характеризация перечислимых множеств. 38. Универсальные вычислимые функции. 39. Существование перечислимого неразрешимого множества. 40. Алгоритмически неразрешимые задачи. Неразрешимость проблемы остановки машины Тьюринга. 41. Сложность алгоритмов. Гипотеза
|
||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.254.177 (0.009 с.) |

 ; б)
; б)  ; в)
; в) 
 ; д)
; д)  ; е)
; е) 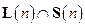 ?
?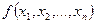 - произвольная булева функция,
- произвольная булева функция,  получена из
получена из  . Определить
. Определить  ; б)
; б)  .
. , то
, то  либо немонотонная, либо несамодвойственная.
либо немонотонная, либо несамодвойственная. и
и  значений переменных, таких что
значений переменных, таких что  , выполняется неравенство
, выполняется неравенство  . Привести пример булевой функции, заданной формулой над множеством монотонно невозрастающих функций, которая не является монотонно невозрастающей.
. Привести пример булевой функции, заданной формулой над множеством монотонно невозрастающих функций, которая не является монотонно невозрастающей. .
. является существенной переменной тогда и только тогда, когда
является существенной переменной тогда и только тогда, когда  полная система; б)
полная система; б)  .
.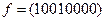 либо 1, либо отрицание.
либо 1, либо отрицание. либо 0, либо отрицание.
либо 0, либо отрицание.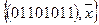 константы 0 и 1.
константы 0 и 1. отрицание.
отрицание. конъюнкцию.
конъюнкцию.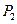 , содержится, по крайней мере, в одном из классов Поста.
, содержится, по крайней мере, в одном из классов Поста.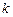 -значной логики.
-значной логики.



