
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Седиментаційний аналіз дисперсності.Содержание книги
Поиск на нашем сайте
Седиментаційний аналіз – це сукупність методів визначання розмірів частинок в дисперсних системах і молекулярної маси макромолекул в розчинах полімерів за швидкістю седиментації. Розглянемо частинку дисперсної фази, що має сферичну форму і рухається в суцільному дисперсійному середовищі. На неї діють сила земного тяжіння спрямована вниз, архімедова сила, спрямована верх і сила тертя, що діє в зворотному до руху частинки напрямку. Fт = mg = rVg (8.18) FАр = r0Vg (8.19) Fтер = 6phru (8.20) u – швидкість осідання частинок. r, r0 - густина дисперсної фази та дисперсійного середовища. Якщо густина частинки дисперсної фази більша за густину дисперсійного середовища, то відбувається осідання частинок, якщо менша, то спливання. Якщо частинка рухається рівномірно, то сили, що на неї діють знаходяться в рівновазі: Fт - FАр = Fтер (8.21) (r - r0)Vg = Вu (8.22) 4/3p r3(r - r0)g = 6phru (8.23) 2 r2(r - r0)g = 9hu (8.24)
За експериментально визначеною швидкістю осідання частинок, та відомими значеннями в’язкості і густини середовища та дисперсної фази, можна розрахувати радіус частинок, що осідають в даний момент часу. Швидкість осідання u розраховують, як відношення висоти освітленого шару рідини h до часу, або маси осаду P до часу: u = h/t; u = Р/t (8.26) В монодисперсному золі всі частинки осідають з однаковою швидкістю. Залежність маси осаду від часу є лінійною (Рис.61,а): P = ut (8.27) Графік залежності маси осаду від часу для бідисперсного золю (Рис.61,б) є ламаною лінією. Продовження відрізків окремих фракцій до перетину з віссю ординат відтворюють на ній відрізки, що відповідають масам цих фракцій.
Рис. 61. Графік осідання монодисперсного (а) та бідисперсного (б) золю. (Q – загальна маса осаду.)
У випадку полідисперсного золю експериментально отриману криву осідання ділять на рівні проміжки часу і проводять дотичні в цих точках до перетину з віссю ординат, отримуючи таким чином маси окремих фракцій, за якими розраховують радіус частинок окремих фракцій. Надалі будують диференційну криву розподілу частинок по їх радіусах, яка дає можливість оцінити скільки частинок і якого розміру присутні в даному золі.
Рис. 62. Крива седиментації полідисперсного золю (а) та диференційна крива розподілу частинок полідисперсного золю по радіусах (б).
Під дією гравітаційного поля осідають тільки досить крупні частинки, частинки колоїдної дисперсності осідають досить повільно. Наприклад частинка кварцу радіусом 0,1 мкм при осіданні у воді пройде шлях в 1 см за 86 год. Для прискорення швидкості осідання А.В.Думанський запропонував використовувати ультрацентрифугу. Ця ідея на практиці була реалізована Т.Сведбергом, який розробив ряд конструкцій ультрацентрифуг з швидкістю обертання десятки тисяч обертів за секунду. Рівняння (8.21) для рівноважного руху частинки у відцентровому полі можна записати наступним чином: Bdx/dt = v(r - r0)w2x (8.28) x - відстань частинки від осі обертання; w – кутова швидкість. Після інтегрування одержуємо:
Розмір частинки дисперсної фази, що осідає відцентровому полі, можна визначити, якщо відомі кутова швидкість, відстань що пройшли частинки та параметри системи.
Приклад 8.2 Розрахувати радіус частинок монодисперсного золю AgCl у воді, якщо час їх осідання у центрифузі склав 10 хв. Початкова відстань частинок від осі обертання 0,09 м, кінцева 0,14 м; густина дисперсної фази 5600 кг/м3; густина дисперсійного середовища 1000 кг/м3; частота обертання центрифуги 1000 об/хв; в’язкість 0,001 Па∙с. Кутова швидкість центрифуги:
Радіус частинок, що осідають розраховуємо за рівнянням:
|
|||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.206.19 (0.008 с.) |

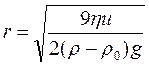 (8.25)
(8.25)

 (8.29)
(8.29) (8.30)
(8.30)




