
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Термодинамічні співвідношення між поверхневим натягом і електричним потенціаломСодержание книги
Поиск на нашем сайте
Утворення рівноважного подвійного електричного шару відбувається самочинно внаслідок переходу частини поверхневої енергії в електричну енергію. З об’єднаного виразу І-го і ІІ-го законів термодинаміки (2.1), при р,T,n=const: dG = sdS + jdq (5.1) Оскільки енергія Гіббса пропорційна екстенсивним величинам, то перейдемо від диференціалів функцій до самих функцій: G = s∙S + j∙q (5.2) Повний диференціал від енергії Гіббса дорівнює: dG = sdS + Sds + jdq + qdj (5.3) Якщо від рівняння (5.3) відняти (5.1), то отримаємо: Sds = -qdj (5.4)
де qs – заряд одиниці поверхні, або густина заряду. Вираз (5.5) має назву перше рівняння Ліпмана. Оскільки знак заряду поверхні і потенціалу завжди співпадають, то при зростання потенціалу поверхневий натяг завжди зменшується. Диференційна ємність ПЕШ, як і будь якого конденсатора дорівнює: Cd = dq/dj (5.6) Підставимо це вираз в перше рівняння Ліпмана і одержимо друге рівняння Ліпмана:
Друге рівняння Ліпмана дає можливість визначення ємності ПЕШ за залежністю поверхневого натягу від потенціалу. Якщо подвійний електричний шар являє собою плоский конденсатор, то його ємність: C = qs/j (5.8) qs = C∙j (5.9) Підставимо цей вираз в перше рівняння Ліпмана, одержуємо: ds/dj = -Cj (5.10) ds = -C∙jdj (5.11) про інтегруємо цей вираз:
при j0=0 одержуємо рівняння електрокапілярної кривої:
Рис. 38. Залежність поверхневого натягу від потенціалу поверхні.
Поверхневий натяг при зміні потенціалу змінюється за рівнянням параболи. Вершина параболи відповідає значенням j0 і smax, а сама парабола симетрична відносно осі ординат. В точці j0 і smax поверхневий шар має нульовий заряд, тобто ПЕШ відсутній. Стан, коли потенціал поверхні рівний нулювідповідає рівності хімічних потенціалів іонів в розчині і на твердій поверхні, що занурена в цей розчин. В 1883 р. Ліпман перевірив рівняння (5.14) на приладі власної конструкції, який він назвав капілярним електрометром, тому це рівняння одержало назву електрокапілярної кривої.
Теорії будови подвійного електричного шару
Теорія Гельмгольца Перрена.
Подвійний електричний шар в теорії Гельмгольца – Перрена (1851 р.) розглядається як плоский конденсатор, одна обкладинка якого безпосередньо зв’язана з твердою поверхнею, а друга, що має протилежний заряд, знаходиться в рідині на дуже малій відстані від поверхні. Потенціал зосереджений в середині подвійного електричного шару і лінійно спадає від j0 до 0, де j0 - потенціал на поверхні твердої частинки:
eа - діелектрична проникність середовища; d - товщина подвійного електричного шару. Головним досягненням теорії є введення поняття „подвійний електричний шар”, який утворюється під дією електростатичних сил. В момент появи теорії не було сформовано таке поняття, як „іон” (поняття „іон” запропонував Арреніус в 1887 р.), а сама теорія не змогла пояснити електрокінетичні явища відомі на той час.
Рис. 39. Схема будови ПЕШ згідно теорії Гельмгольца – Перрена.
Теорія Гуї - Чепмена
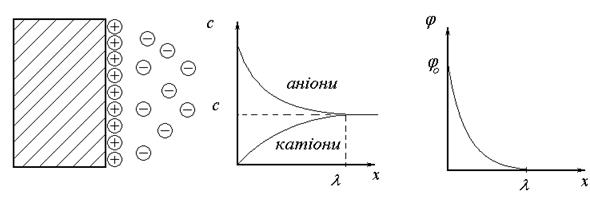
У 1910 р. Гуї і 1913 р. Чепмен незалежно один від одного розробили теорію будови подвійного електричного шару з дифузійним шаром протиіонів. Згідно цієї теорії в подвійному електричному шарі крім електростатичних сил діють також сили теплового руху, які прагнуть розподілити протиіони рівномірно в об’ємі. Біля твердої поверхні, на якій знаходяться потенціалвизначальні іони, переважають електростатичні сили, які прагнуть притягнути протиіони, тому їх концентрація тут велика. З відстанню дія цих сил зменшується і концентрація цих іонів теж зменшується і на деякій відстані стає рівною концентрації іонів в розчині. Ця відстань є товщиною подвійного електричного шару l (рис.40). Іони того ж знаку, що й потенціалвизначальні відштовхуються електростатичними силами від поверхні, тому їх концентрація тут значно менша і поступово зростає з відстанню. На великих відстанях від поверхні: с+ = с- =с∞
Рис. 40. Схема будови ПЕШ згідно теорії Гуї – Чепмена.
На малих відстанях від поверхні концентрація позитивних і негативних іонів описується законом розподілу Больцмана:
с ∞ - концентрація іонів в розчині; WX – робота по переміщенні іонів на відстань х від поверхні; z – заряд іона; jx – потенціал на відстані х від поверхні. Співвідношення між потенціалом j та об’ємною густиною заряду r для сферичного електричного поля визначається рівнянням Пуасона: ∂2j/∂x2 + ∂2j/∂y2 + ∂2j/∂z2 = -r/ea (5.18) Для плоского подвійного електричного шару можна розглядати зміну потенціалу тільки по нормалі до поверхні, тому розглядаємо зміну потенціалу тільки по одній координаті: ∂2j/∂x2 = -r/ea (5.19) Об’ємну густину заряду можна представити, як: r = F(z+c+ - z-c-) (5.20) r = Fc∞Sziexp(jxziF/RT) (5.21) Підставимо це рівняння в рівняння Пуасона одержуємо рівняння Пуасона-Больцмана:
При малих значеннях потенціалу поверхні (j <25 мВ), (jxziF/RT)<< 1, розв’язок рівняння Пуасона-Больцмана має вигляд: jx = joe-c∙x (5.23) Де c згідно теорії сильних електролітів Дебая – Гюккеля величина обернена до товщини іонної атмосфери:
Для великих значень потенціалу (jxziF/RT)> 1
Згідно рівняння 5.21 заряд і потенціал поверхні взаємо пропорційні, тому ПЕШ можна вважати плоским конденсатором, відстань між пластинами якого дорівнює:
Товщина подвійного електричного шару зменшується з ростом концентрації іонів. Зростання температури приводять до збільшення швидкості руху іонів і збільшення товщини подвійного електричного шару. На відстані l потенціал поверхні jo зменшується в е=2,718 рази. jx = joe-cl = joe-c∙1/c = joe-1 = jo/e (5.28) При переміщені дисперсної фази відносно дисперсійного середовища межа ковзання знаходиться на якійсь відстані D від поверхні. Потенціал на межі ковзання називається електрокінетичним потенціалом, або z- (дзета) потенціалом. Величина z - потенціалу, на відміну від потенціалу поверхні jo, залежить від концентрації і валентності індиферентних іонів в розчині.
Рис. 41. Залежність потенціалу від відстані при різних концентраціях електроліту.
Теорія Гуї - Чепмена не враховує розміри іонів та вплив адсорбційних сил на структуру ПЕШ. Це призвело до суттєвих розбіжностей між розрахунковими та експериментально визначеними параметрами ПЕШ. Ця теорія неспроможна пояснити явище перезарядки та різний вплив іонів ліотропного ряду.
Приклад 5.1 Розрахуйте товщину дифузійного іонного шару на поверхні сульфату барію, що знаходиться в водному розчині NaOH з концентрацією 25 мг/л. Відносна діелектрична проникність розчину 82,2 при температурі 288 К. Розрахуємо молярну концентрацію розчину: c = 25∙10-3[г/л] /58,44 [г/моль] = 4,28∙10-4 моль/л = 0,428 моль/м3. Товщину дифузійного іонного шару розраховуємо за рівнянням λ = (εε0RT/ F2∑cz2)1/2 = = ((82,2∙8,85∙10-12∙8,314∙288)/(2 965002∙1/2 0,428(1∙12 + 1∙12)))1/2 = 1,477∙10-8 м = 14,77 нм. Приклад 5.2 Визначте значення потенціалу дифузійного шару для слабозарядженої поверхні на відстані 15 нм від поверхні. Середовище, що оточує поверхню - водний розчин NaCl з концентрацією 5∙10-4 моль/л, температура 293 К. Відносна діелектрична проникність середовища 80,1; потенціал поверхні 0,02 В. c = (F2∑cz2 / εε0RT)1/2 = (965002∙0,5(1∙12+1∙12) /∙80,1∙8,85∙10-12 8,314∙293)1/2 = = 73,43∙106 м-1 φx = φ0е-cx = 0,02∙е – 0,0734 ∙15∙ = 0,02∙е – 1,10 = 6,7 мВ Приклад 5.3 Розрахуйте ємність дифузійного шару дисперсної фази. Дисперсійне середовище – водний розчин СаСl2 з концентрацією 2∙10-4 моль/л і відносною діелектричною проникністю 83,8, при температурі 283 К. С = ε ε0/ λ = ε ε0 /(εε0RT / F2∑cz2)1/2 = = 83,8∙8,85∙10-12/(83,8∙8,85∙10-12∙8,314∙283/(965002∙0,2∙(22+2∙12)))1/2=59,4∙10-3 ф/м2
5.4.3. Теорія Штерна.
У 1924 р. Штерн запропонував теорію будови подвійного електричного шару, в якій він використав уявлення попередніх теорії. При цьому він зробив два посилання: - реальні іони мають конкретні розміри і не можуть підходити до твердої поверхні на відстань ближче ніж іонний радіус. - в системі діють сили адсорбційного і електростатичного притягання та сили відштовхування, зумовлені тепловим рухом. Згідно з теорією Штерна, частина протиіонів притягується до твердої поверхні як електростатичними, так і адсорбційними силами. Дія адсорбційних сил, на відміну від електростатичних, швидко спадає з відстанню, тому їх вплив слід враховувати тільки біля самої поверхні твердого тіла (на відстані декілька ангстрем). Внаслідок цього частина протиіонів утримується на дуже близькій відстані біля поверхні, утворюючи плоский конденсатор товщиною d, аналогічний описаному у теорії Гельмгольца - Перрена. В цьому шарі спостерігається різке лінійне падіння електричного потенціалу. Цей шар називається гельмгольцівським, або адсорбційним шаром. Решта протиіонів, необхідних для компенсації заряду потенціалвизначальних іонів, внаслідок теплового руху розподілені в об’ємі розчину поблизу поверхні і утворюють шар, в якому вони підпорядковуються тим самим законам, що і в теорії Гуї - Чепмена. Цю частину подвійного електричного шару товщиною l, називають дифузійним шаром, або шаром Гуї. В дифузійному шарі потенціал спадає за експонентою і не так стрімко, як в адсорбційному.
Рис. 42. Схема будови ПЕШ згідно теорії Штерна.
jo - потенціал на поверхні частинки jd - потенціал адсорбційного шару d - товщина адсорбційного шару l - товщина дифузійного шару При русі частинок дисперсної фази на поверхні яких утворився ПЕШ межа ковзання між рухомою і нерухомою фазою знаходиться на деякій відстані D відтвердої поверхні, яка не співпадає з межею адсорбційного і дифузійного шарів. Потенціал на межі ковзання між рухомою і нерухомою фазою називають електрокінетичним, або z – потенціалом. Згідно з теорією Штерна заряд твердої поверхні q дорівняє сумі зарядів протиіонів адсорбційного qа, та дифузійного шарів qд. q = qа + qд (5.29) Для характеристики кількості іонів, адсорбованих одиницею поверхні Штерна, використав уявлення теорії адсорбції Ленгмюра. Для симетричного електроліту він одержав наступні рівняння:
q+, q- - специфічні адсорбційні потенціали катіону та аніону. Заряд адсорбційного шару є різницею зарядів катіонів та аніонів, що припадають на одиницю поверхні. qa = Fz(A+ - A-) (5.32)
Заряд дифузійного шару безпосередньо пов’язаний з потенціалом в цьому шарі і розраховується за теорією Гуї – Чепмена:
Сумарний заряд подвійного електричного шару дорівнює
Концентрація індиферентного електроліту в розчині сильніше впливає на заряд адсорбційного шару, ніж на заряд дифузійного. Тому при зменшенні концентрації структура ПЕШ наближається до моделі Гуї – Чепмена, при цьому товщина ПЕШ зростає (рис.43). Зі збільшенням концентрації електроліту структура подвійного електричного шару наближається до моделі Гельмгольца-Перрена, а товщина ПЕШ буде зменшуватися до адсорбційного шару. При цьому z - потенціал буде спадати, поступово наближаючись до нуля (рис.43), стан ПЕШ коли z - потенціал дорівнює нулю називається ізоелектричним.
Рис. 43. Залежність z - потенціалу від концентрації. Вплив природи протиіонів на структуру і товщину ПЕШ, визначається їх валентністю та адсорбційним потенціалом. Чим більша валентність іонів та їх адсорбційний потенціал, тим сильніше вони втягуються в адсорбційний шар, і тим сильніше стискається ПЕШ. Електрична ємність ПЕШ визначається, як ємність двох послідовно з’єднаних конденсаторів: 1/С = 1/Са + 1/Сд (5.36) Товщина і ємність адсорбційного шару Са, майже не залежить від концентрації електроліту, в той час, як товщина і ємність дифузійного шару Сд сильно залежить від неї. Якщо ємність одного з конденсаторів значно більша за ємність другого, то їх сумарна ємність дорівнює меншому значенню, тому ємність ПЕШ для розведених розчинів дорівнює ємності дифузійного шару, а для концентрованих – адсорбційного.
|
||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 546; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.50.170 (0.008 с.) |

 (5.5)
(5.5)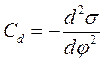 (5.7)
(5.7) (5.12)
(5.12) (5.13)
(5.13) (5.14)
(5.14)
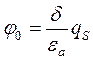 (5.15)
(5.15)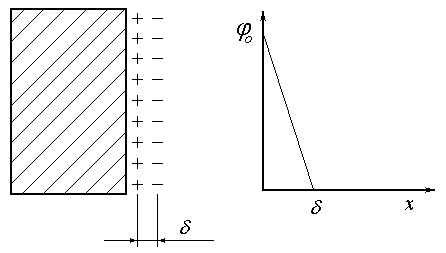
 (5.16)
(5.16)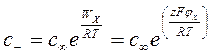 (5.17)
(5.17)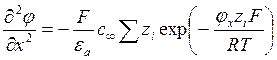 (5.22)
(5.22) (5.24)
(5.24)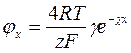 (5.25)
(5.25)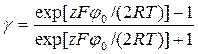 (5.26)
(5.26) (5.27)
(5.27)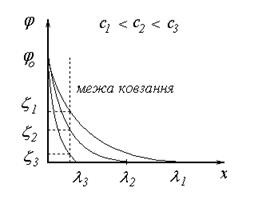

 (5.30)
(5.30)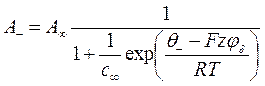 (5.31)
(5.31)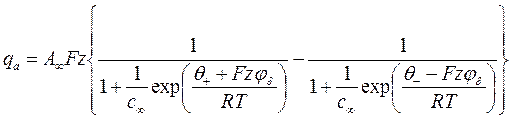 (5.33)
(5.33) (5.34)
(5.34) (5.35)
(5.35)



