
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсність і реакційна здатність речовинСодержание книги
Поиск на нашем сайте
Під реакційною здатністю речовин розуміють їх здатність вступати в хімічні реакції, або змінювати агрегатний стан. Реакційна здатність характеризується енергією Гіббса:
dG=-SdT+Vdp, (3.16) при T=const dG=Vdp, або DG=VDp, для частиноксферичної форми Dp=2s/r, звідси DG=±2sV/r (3.17) плюс або мінус в рівнянні відповідають додатній, або від’ємній кривизні поверхні. Реакційна здатність речовини прямо пропорційна до кривизни поверхні, і обернено пропорційна до її лінійного розміру.
Тиск насиченої пари над викривленою поверхнею
Додаткова зміна енергії Гіббса, що пов’язана з дисперсністю, дорівнює:
р, р∞ - тиск пари над викривленою і рівною поверхнею, відповідно. Підставивши рівняння (3.17) в (3.18) одержуємо:
Рівняння (3.20) називають рівнянням Кельвіна (Томсона) Тиск пари над краплею буде тим більший, чим більша кривизна поверхні, або чим менший радіус краплини. У випадку від’ємної кривизни, яка наприклад виникає в капілярах при змочуванні тиск пари над викривленою поверхнею зменшується зі збільшенням кривизни поверхні або зі зменшенням радіуса. Тому конденсація пари в капілярі відбувається при тиску меншому ніж над рівною поверхнею і рівняння Кельвіна часто називають рівнянням капілярної конденсації.
Приклад 3.3 Обчисліть тиск насиченої пари над краплями води з дисперсністю 0,1 нм-1 при температурі 293К. Тиск парів води над плоскою поверхнею при цій температурі 2338 Па, густина води 998 кг/м3, поверхневий натяг 72,7 мДж/м2. Вплив кривизни поверхні на тиск насиченої пари виражається рівнянням Кельвіна
ln(p/p∞) = (2∙0,0727∙18∙10-3∙2∙108)/(8,314∙293∙988) = 0,21 p/p∞ = exp(0.21) =1,23; p = 1,23∙2338 = 2875 Па
Приклад 3.4 Обчисліть тиск пари над увігнутим меніском в капілярі радіусом 1 мкм при 293 К. Кут змочування дорівнює нулю. Густина води 0,998 г/см3, тиск пари над макрофазою 2338 Па, поверхневий натяг води 72,75 мДж/м2.
ln(p/p∞) = (2∙72,75∙10-3∙18∙10-6)/(8,314∙293∙1∙10-6) = -1,075∙10-3 p/p∞ = exp(-1,075∙10-3) =0,9989 p = 0,9989∙2338 = 2335 Па
Вплив дисперсності на температуру фазового переходу
Зміна енергії Гіббса, яка пов’язана з дисперсністю дорівнює: DG = DH - TDS = 2sV/r (3.21) для фазового перетворення зміна ентропії дорівнює: DSфп=DHфп/T∞ (3.22)
де Т, Т∞ - температура фазового переходу дрібних та крупних частинок.
Із ростом дисперсності або подрібненості температура фазового переходу зменшується. Причому важкотопкі речовини дають більш сильний ефект пониження температури з ростом дисперсності ніж легкоплавкі. Цей ефект широко застосовується в порошковій металургії, та при виробництві кераміки. Він є більш помітним при високих температурах плавлення (Табл.5). Таблиця 5 Залежність температури плавлення калію і срібла від дисперсності.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.63.214 (0.009 с.) |

 , де (3.18)
, де (3.18) (3.19)
(3.19) (3.20)
(3.20)

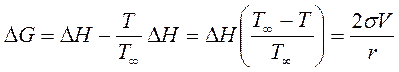 , (3.23)
, (3.23) (3.24)
(3.24)


