
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Молекулярно – кінетичні властивості дисперсних системСодержание книги
Поиск на нашем сайте
8.1.1. Броунівський рух
Тепловий рух частинок дисперсної фази ультрамікрогетерогенних систем називають - броунівським рухом. Кожна частинка дисперсної фази отримує безліч поштовхів з боку молекул дисперсійного середовища. Якщо частинка досить мала, то кількість поштовхів, які вона отримує одночасно з різних сторін не є однаковою і тому частинка отримує періодичні імпульси, що примушують її рухатися за складною траєкторією. Інтенсивність руху частинок дисперсної фази сильно залежить від їх розмірів і маси. Чим більшою за розмірами є частинка, тим повільніше вона рухається. Частинки розміром біля 5 мкм, здійснюють рухи, що сприймаються, як коливання навколо якогось центру. Частинки з розміром більшим за 5 мкм практично не приймають участь у броунівському русі. Зв’язок між рухом частинок та їх молекулярно кінетичними властивостями було встановлено Ейнштейном та Смолуховським. Для кількісної характеристики броунівського руху вони запропонували використовувати поняття проекції середньо квадратичного зміщення частинки у вибраному напрямку, тому що при спостереженні за частинками дисперсної фази, ми фіксуємо не реальну траєкторію їх руху, а положення частинок в певний момент часу.
Dі – окремі проекції зсуву частинки.
Рис. 59. Схема броунівського руху частинки.
8.1.2. Дифузія.
Дифузією називають самочинний процес переносу речовини, зумовлений вирівнюванням її концентрації в початково неоднорідній системі. Дифузія відбувається внаслідок теплового руху молекул, або більш крупних частинок речовини, наприклад частинок дисперсної фази в колоїдних системах. Найбільш інтенсивна дифузія в газах, де коефіцієнт дифузії при 293 К має порядок 10-4 м2/с, в рідинах і твердих тілах відповідно 10-9 і 10-12 м2/с. Причиною виникнення дифузії є наявність в системі градієнта концентрації dс/dx, який спричиняє потік речовини в напрямку його зменшення, інтенсивність якого пропорційна величині градієнта концентрації. Цю залежність описує перший закон дифузії Фіка,:
m - кількість речовини, що дифундувала через площу S за час t; D - коефіцієнт дифузії. Коефіцієнт дифузії можна розрахувати за рівнянням Ейнштейна:
Якщо рух частинок підпорядковується закону Стокса, то коефіцієнт тертя дорівнює:
B = 6prh (8.4) r - радіус частинок; h - в’язкість середовища. За відомими значеннями D, h, T можна розрахувати радіус частинок: r = kT/(6phD) (8.5) Зв’язок між середнім квадратичним зміщенням частинки і коефіцієнтом дифузії довели незалежно один від одного А.Ейнштейн і М.Смолуховський. Розглянемо трубку з поперечним перерізом S, що заповнена колоїдним розчином концентрація якого спадає зліва направо с1>с2.
Рис. 60. Схема переносу речовини при дифузії.
Маса речовини, що буде перенесена в процесі дифузії, може бути розрахована за рівнянням: m = m1-m2 = ½Dс1S - ½Dс2S = ½D(с1-с2)S (8.6) Градієнт концентрації дорівнює: dс/dx = -(с1-с2)/D (8.7) с1-с2 = -D(dс/dx) (8.8) Підставимо цей вираз в рівняння (8.7): m = -½D2(dс/dx)S (8.9) Прирівняємо цей вираз з рівнянням Фіка, одержуємо:
D2 = 2D∙t (8.11) Об’єднаємо це рівняння з рівнянням Ейнштейна і одержуємо рівняння Ейнштейна – Смолуховського.
Середнє квадратичне зміщення збільшується з ростом температури і зменшується з ростом розмірів частинок та в’язкості середовища. Це рівняння одержало надійне експериментальне підтвердження в роботах Т. Сведберга та Зедднига. Теоретичні та експериментальні докази теплової природи броунівського руху довели, що колоїдні системи підпорядковуються тим самим законам молекулярно-кінетичної теорії, що і молекулярні системи.
Приклад 8.1 Обчислити середнє зміщення колоїдних частинок гідроксиду заліза (III) при 293 К за 4 с, якщо радіуси частинок дорівнюють 10-8 м, а в’язкість води 10-3 Па∙с. Величину середнього зміщення знаходимо за рівнянням:
|
|||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.231.160 (0.01 с.) |

 (8.1)
(8.1)
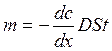 (8.2)
(8.2) (8.3)
(8.3)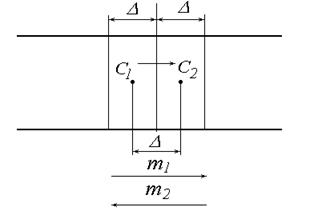
 (8.10)
(8.10)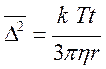 (8.12)
(8.12)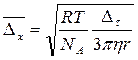 =
= 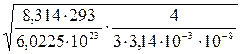 = 1,32∙10-5 м.
= 1,32∙10-5 м.


