Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принципи формування поверхневого шаруСодержание книги
Поиск на нашем сайте
Згідно принципу Гіббса – Кюрі термодинамічно стійкою є форма тіла з мінімальною поверхневою енергією, тому кожна система прагне досягнути мінімального значення поверхневої енергії. Математично це записується, так:
SsiSi=min (V=const) (2.24)
Рідини є ізотропними, тобто мають однакові властивості у всіх точках поверхні s=const, тому для рідин: sSSi=min (V=const) (2.25)
Рідкі тіла зменшують свою поверхневу енергію, за рахунок зменшення площі міжфазної поверхні. Очевидно, що більш термодинамічно стійкою формою рідини є форма з мінімальною поверхнею, тобто сфера. Рідини здатні зменшувати свій поверхневий натяг також за рахунок відповідної орієнтації молекул поверхневого шару. Молекули орієнтуються таким чином, щоб максимально зменшити міжфазний поверхневий натяг. Наприклад молекули органічних речовин, що знаходяться в поверхневому шарі на межі з повітрям виштовхують на зовні неполярний вуглецевий радикал і ховають в об’ємі полярні функціональні групи. Тому багато органічних сполук мають приблизно однаковий поверхневий натяг (табл. 3). Таблиця 3 Поверхневий натяг органічних речовин на межі з повітрям при 298К.
Кристали є анізотропними, тому кожна їх грань має характерне для неї значення поверхневого натягу. При формуванні кристалів в рівноважних умовах надлишковий тиск під всіма гранями є однаковим і виражається законом Вульфа. Dp=2si/li=const (2.26) Dp - Надлишковий тиск під гранню кристалу si - Питома поверхнева енергія грані li - Відстань від грані до центра кристалу Чим далі від центра знаходиться грань кристалу, і чим меншу поверхню вона має, тим більша її поверхнева енергія. Крім означених факторів поверхнева енергія конденсованих речовин може зменшуватися за рахунок адсорбції речовин, які зменшують поверхневий натяг.
2.6. Адгезія, когезія
Взаємодію між поверхнями конденсованих тіл різної природи називають адгезією або прилипанням. Адгезійні взаємодії виникають при контакті двох конденсованих тіл, якщо відстань між ними співмірна з міжмолекулярною. Притягання молекул і атомів всередині окремої фази називають когезією або злипанням. Це явище обумовлене міжмолекулярними силами притягання. Робота когезії визначається затратою енергії на оборотній розрив тіла по перерізу рівному одиниці площі. При розриві тіла утворюються дві поверхні, тому: WK=2s (2.27) Розглянемо зміну енергії Гіббса системи, яка у вихідному стані складається з двох конденсованих тіл 2 і 3, що знаходяться в газовій фазі 1, з поверхневими натягами s2,1 i s3,1.
Рис. 7. Взаємодія між тілами різної природи.
Gпоч=s3,1+s2,1 (2.28) Після адгезійної взаємодії (рис.7) між тілами 2 і 3: Gкін=s3,2 (2.29) Робота адгезії дорівнює: Wa = -DG = Gпоч-Gкін=s3,1+s2,1-s3,2 (2.30)
Рівняння (2.30) називають рівнянням Дюпре. Чим більша міжфазна взаємодія, тобто робота адгезії, тим менший міжфазний натяг. Коли міжфазний натяг s3,2=0, міжфазна поверхня зникає, що відбувається при повному розчиненні. Звідси витікає умова розчинення.
Wa≥s3,1+s2,1 (2.31) Wa≥(2s3,1+2s2,1)/2=(WK1+WK2)/2 (2.32) Таким чином умова розчинення полягає в тому, що робота адгезії повинна бути рівна або більша за середню величину роботи когезії тіл, що взаємодіють.
Змочування і розтікання
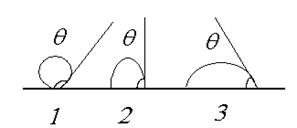
Змочування – це поверхневе явище, яке полягає у взаємодії рідини з іншою конденсованою фазою, при умові одночасного контакту трьох фаз, одна з яких - газ (повітря). Мірою змочування є крайовий кут змочування, це кут між площиною поверхні, що змочується і дотичною до поверхні рідини в одній із точок контуру змочування. В залежності від величини крайового кута змочування можливі наступні варіанти контакту рідини з поверхнею (рис.8).
Рис. 8. Приклади змочування поверхні. 1. 180о>q>90o Поверхня не змочується (ліофобна); 2. q=90o Межа змочування і незмочування; 3. q<90o Поверхня змочується (ліофільна). Проаналізуємо поверхневі сили, що діють на краплину яка знаходиться на поверхні в умовах рівноваги (рис.9).
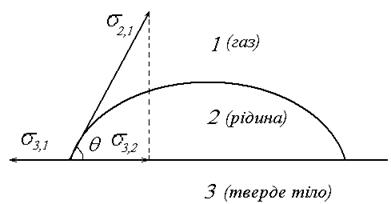
Рис. 9. Сили, що діють на краплю на поверхні.
s3,1 - сила, яка діє між твердим тілом і газом і прагне розтягнути краплю; s3,2 –стягує краплю і діє між рідиною і твердим тілом; s2,1 – діє між газом і рідиною. У випадку рівноваги цих сил: s3,1=s2,1cosq+s3,2 (2.33)
Рівняння (2.34) називають рівнянням Юнга. s3,1- s3,2=s2,1cosq (2.35) Підставимо вираз (2.35) в рівняння Дюпре (2.30) і 1 отримуємо рівняння Дюпре - Юнга: Wa=s3,1- s3,2+s2,1cosq=s2,1+s2,1cosq=s2,1(1+cosq) (2.36) Розділимо вираз (2.36) на 2s2,:
Якщо q=0o cosq=1 Wa=WK; q=90o cosq=0 Wa=0,5WK; q=180o cosq=-1 Wa=0, але такого стану в природі не спостерігалось. Наприклад в системі вода-тефлон: q=108o; sH2O=72мДж/м2; Wa=50,3мДж/м2.
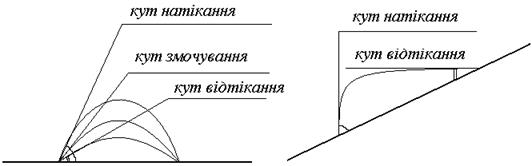
На поверхнях реальних тіл завжди є неоднорідності, пори та тріщини. Вони викликають відхилення кутів змочування від рівноважних значень. Це відхилення називають гістерезисом змочування. При наявності гістерезиса змочування розрізняють граничні кути натікання і відтікання. При збільшенні об’єму краплини максимальний кут, при якому площа поверхні, яку займає крапля, не змінюється називають кутом натікання; а при зменшенні об’єму краплини мінімальний кут при якому площа поверхні що займає краплина залишається незмінною називають кутом відтікання. За утворенням цих кутів зручно спостерігати нахиляючи пластину з краплею, до моменту стікання її з поверхні (рис.10).
Рис. 10. Змочування реальних тіл.
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.60.175 (0.007 с.) |


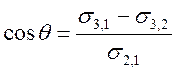 (2.34)
(2.34)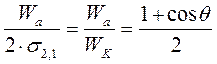 (2.37)
(2.37)