
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изменение энтропии в необратимых процессахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ранее мы рассмотрели равновесные, обратимые процессы, при совершении которых в прямом и обратном направлении не происходит остаточных изменений ни в самой системе, ни в окружающей среде. Любой реальный процесс является в большей или меньшей степени неравновесным. (Если, например, быстро увеличить температуру окружающей среды, то газ в цилиндре будет постепенно прогреваться, релаксируя к состоянию равновесия, соответствующему новым параметрам окружающей среды. В процессе релаксации газ не находится в равновесии с окружающей средой, и его нельзя характеризовать уравнением состояния.) Неравновесные процессы необратимы. При проведении таких процессов в прямом и обратном направлениях либо система, либо окружающая среда не возвращается в исходное состояние. Рассмотрим принципиальные отличия необратимых процессов от обратимых на примере расширения газа в цилиндре под поршнем (рис. 11).
 а изменение энтропии dsобр а изменение энтропии dsобр  = =  /T. /T.
Невыполнение хотя бы одного из указанных условий делает расширение газа необратимым. - Если необратимость вызвать трением поршня о стенки цилиндра, то работа - Если необратимость вызвана отсутствием механического равновесия (P < pF), то поршень будет двигаться ускоренно, что приводит к появлению вихрей в газе, затухающих под действием внутреннего трения, в результате часть работы опять превратится q тр. Работа снова получается меньше, а возрастание энтропии больше, чем в обратимом процессе. -Если необратимость вызвана теплообменом при конечной разности температур (температура газа T < T 1 (источника.)), то возрастание энтропии ds Итак, необратимость всегда приводит к увеличению энтропии рабочего тела при том же количестве подведенной теплоты и к потере части работы.
Для изолированных систем эти выражения принимают вид: ds ≥0. Если в адиабатно-изолированной системе осуществляются равновесные процессы, то энтропия системы остается постоянной. Самопроизвольные (а значит необратимые) процессы в изолированной системе всегда приводят к увеличению энтропии. Это и есть формулировка второго начала термодинамики для неравновесных процессов, известная под названием принципа возрастания энтропии.
Цикл Карно Для того чтобы шире раскрыть содержание 2-го закона термодинамики, необходимо исследовать круговые процессы-циклы. Начало теоретическому изучению циклов положил французский физик и инженер Карно. Он сформулировал условия, при которых возможно преобразование теплоты в работу. Рассмотрим предложенный им цикл, который решает вопрос о том, какая максимальная доля тепла при заданных условиях может быть превращена в механическую работу. Пусть рабочее тело находится в непроводящем тепло цилиндре, имея однако возможность в необходимых случаях приходить в соприкосновение с двумя источниками тепла с температурами T 1 и T 2 (рис. 12). Считаем, что теплоемкости источников столь велики, что отбор рабочим телом теплоты от одного источника и передача ее другому практически не меняет их температуры. Начальное состояние характеризуется точкой A. Приводим цилиндр в соприкосновение с горячим источником теплоты. От этого состояния начинается изотермический процесс расширения АВ. Количество подводимой теплоты определяется как: q 1 = T 1 (s 2- s 1)
Затем в точке В устраняется тепловой контакт между газом и источником, и дальнейшее расширение газа происходит адиабатно (без теплообмена с окружающей средой) за счет изменения внутренней энергии газа. При этом температура газа уменьшается. В точке C газ приводится в тепловой контакт с холодным теплоприемником T 2 и дальнейшее состояние рабочего тела связано с необходимостью возвращения поршня в первоначальное положение, а газа в начальное состояние. Это осуществляется путем изотермического сжатия с передачей теплоты q 2 от газа к теплоприемнику: q 2= T 2(s 2- s 1). В точке D рабочее тело изолируется от теплоприемника и дальнейшее сжатие происходит без теплообмена, т. е. адиабатически. Температура газа возрастает, пока не достигнет значения T 1, а газ не приходит в исходное состояние, соответствующее точке A.
На p-v и T-s диаграммах цикл выглядит следующим образом (рис. 13):
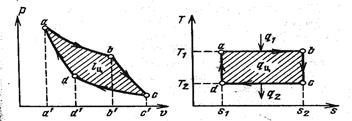
Работа расширения на диаграмме будет площадь АВСС´А´. Количество подведенной теплоты будет выглядеть изотермой АВ, а тепло будет измерено прямоугольником АВS2S1. Алгебраическая сумма работ расширения и сжатия измеряет работу, совершенную рабочим телом за цикл l ц. Теплота, полезно используемая в цикле, равна q 0= q 1– q 2, измеряется в T-s диаграмме площадью прямоугольника АВСD. Термический КПД: ηt= ηt= а т. к. площади прямоугольников имеют одинаковые основания, то на основании теории подобия можно записать уравнение в виде ηt= Формула КПД цикла Карно отражает содержание второго закона термодинамики. Из нее видно, что теплоту горячего источника можно было бы полностью превратить в работу, если можно было бы получить T 1 → Выведенный нами термический КПД цикла Карно относится к обратимому круговому процессу, состоящему из обратимых термодинамических процессов. Необратимость процесса связана с потерей работы, и поэтому η t необратимого цикла всегда меньше обратимого. Обратный цикл Карно Рассмотрим обратимый цикл Карно в обратном направлении (рис. 14):
Рис.14
Рабочее тело с параметрами точки A расширяется адиабатно и охлаждается от температуры T 1 до T 2. На p-v -диаграмме это изображается кривой AD. Затем расширение идет изотермически с получением тепла q 2 от холодного источника T 2. После чего начинается сжатие газа сначала адиабатически (кривая CB) с увеличением температуры от T 2 до T 1, а затем изотермически (BA) с отводом тепла q 1 к теплоприемнику с температурой T 1 (T 1> T 2). В результате цикла за счет затраченной извне механической работы (энергии) от источника отнимается теплота q 2 с низкой температурой T 2 и отдается теплота q 1 теплоприемнику с высокой температурой T 1 , т. е.
q1= q2+ lц
Работа, затраченная на осуществление обратного цикла Карно, равна по абсолютной величине работе прямого цикла, но имеет обратный знак. Машина, осуществляющая обратный цикл Карно, называется холодильной машиной. Эффективность работы холодильной машины характеризуется холодильным коэффициентом:
Заметим: чем меньше разность (T 1- T 2) между холодильной камерой и окружающей средой, тем меньше нужно затратить энергии для передачи теплоты от холодного тела к горячему и тем выше холодильный коэффициент.
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 659; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.158.34 (0.01 с.) |

 Расширение будет обратимым (равновесным) только в том случае, если: температура газа равна температуре теплоисточника T=T 1, внешняя сила уравновешена давлением газа на поршень P=pF, и при расширение газа нет ни внешнего, ни внутреннего трения.
Расширение будет обратимым (равновесным) только в том случае, если: температура газа равна температуре теплоисточника T=T 1, внешняя сила уравновешена давлением газа на поршень P=pF, и при расширение газа нет ни внешнего, ни внутреннего трения. оказывается меньше чем pdυ, т. к. часть её в результате трения переходит в теплоту q тр. Она воспринимается газом вместе с подводимой теплотой
оказывается меньше чем pdυ, т. к. часть её в результате трения переходит в теплоту q тр. Она воспринимается газом вместе с подводимой теплотой  оказывается больше, чем в обратимом.
оказывается больше, чем в обратимом. оказывается больше чем ds обр=
оказывается больше чем ds обр= 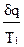 из-за снижения температуры газа.
из-за снижения температуры газа. Рис. 12
Рис. 12 , или можно записать через площади
, или можно записать через площади ,
, .
. или T 2=0. Но оба значения таких температур недостижимы. Значит КПД=1 получить нельзя.
или T 2=0. Но оба значения таких температур недостижимы. Значит КПД=1 получить нельзя.
 .
.


