
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Термодинамические газовые процессыСодержание книги
Поиск на нашем сайте
Задача исследования состоит в определении теплоты и работы того или иного процесса, а также изменения основных термодинамических функций, т.е. внутренней энергии, энтальпии и энтропии. Основными процессами в теоретическом и прикладном отношениях являются: - изохорный (протекающий при постоянном объеме); - изобарный (протекающий при постоянном давлении); - адиабатный (процесс, при котором отсутствует тепло-обмен с окружающей средой); - политропный (удовлетворяющий уравнению pυ n=const). Рассмотрим каждый из этих процессов в отдельности.
Изохорный процесс При изохорном процессе выполняется условие: v = const. Из уравнения состояния идеального газа pv=RT следует, что т. е. давление газа прямо пропорционально его абсолютной температуре:
График этого процесса будет выглядеть следующим образом (рис. 15):
Рис. 15 Так как dv = 0, то работа расширения q Так как
∆u= cυ(t 2 -t1).
Изменение энтропии определяется:
s 2 -s 1 =cυ ln (p 2 /p 1 )= cυ ln (T 2 /T 1 ).
Из полученных результатов видно, что работа изохорного процесса равна нулю, а теплота равна изменению внутренней энергии газа.
Изобарный процесс, протекает при p =const. Из уравнения состояния идеального газа находим:
т. е. объем газа пропорционален его абсолютной температуре. Графики процесса в p-v и T-s координатах (рис. 16):
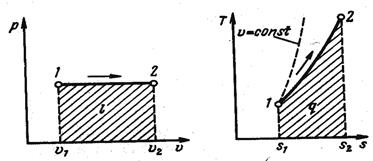
Из выражения, l=p(υ2-υ1),
а т. к. pυ1=RT1 и p2υ2=RT2 , то
l=R(T 2 -T 1 ),
количество теплоты, сообщаемое газу, будет равно:
Изменение энтропии:
s2-s1=cpln(υ2/υ1)= cpln(T2/T1).
Это тоже логарифмическая характеристика, но поскольку с p> с v, то изобара идет более полого, чем изохора. Изотермический процесс При изотермическом процессе Т =const, значит pv = RT =const или
т. е. давление и объем обратно пропорциональны друг другу. График процесса выглядит следующим образом (рис.17):

Так как температура не изменяется, то внутренняя энергия остается постоянной, а
l=p 1 v 1ln (υ 2 /υ 1 )=p 1 v 1ln (p 1 /p 2 ); l=RT ln (υ2/υ1);
Изменение энтропии выражается так:
Адиабатный процесс, происходит без теплообмена, для него
и du= -pdυ, di=υdp. Уравнение адиабаты pv k=const Уравнение первого закона термодинамики принимает вид:
сpdT - υdp=0 и сυdT + pdυ=0.
Поделив первое уравнение на второе, получим: Если проинтегрируем последнее выражение при условии, что k После потенцирования имеем:
Это уравнение адиабаты, а величина Теплоемкость газов не зависит от температуры, поэтому и k тоже не зависит от температуры и определяется лишь числом степеней свободы молекулы. Для одноатомного газа k =1,66, для двухатомного k =1,4, для трех и многоатомных газов k =1,33. Соотношения между параметрами состояния в адиабатном процессе имеют вид:
Работа расширения при адиабатном процессе согласно первому закону термодинамики совершается за счет уменьшения внутренней энергии и вычисляется:
т. к. p1υ1=RT1 и p2υ2=RT2 , то
Так как теплообмена газа с окружающей средой нет, то q=0, На диаграмме (рис.18)
Рис.18 Политропным называется процесс, который описывается уравнением pvn= const. Следовательно, все рассмотренные выше процессы являются частными случаями политропного процесса. Показатель политропы n может меняться от -∞ до +∞, но для данного процесса является величиной постоянной. Покажем на графиках (рис. 19) в p-v и T-s координатах политропы, изображающие политропические процессы изменения состояния газа для частных значений n при расширении. Сопоставляя уравнения рассмотренных процессов можно установить, что n имеет следующие значения в отдельных процессах: для изобарного процесса n= 0, c n =c p, изотермического процесса n= 1, c n =∞, адиабатного процесса n=k, c n=0, изохорного процесса n= ±∞, c n= c v, где c n– удельная теплоемкость газа в политропном процессе:
сn=сυ(n-k)/n- 1 )
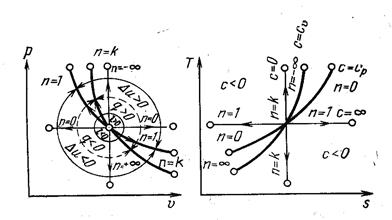
По кривым можно определить расположение политропы и при других значениях n, а также найти знак для q и ∆ u. Из уравнения политропы и уравнения состояния можно получить выражения, устанавливающие связь между p, v и T в любых точках на политропе:
Работа расширения газа в политропном процессе ℓ
=∫pdυ, ℓ=R(T 2 -T 1 )/( 1 -n).
Количество теплоты
q=(u 2 -u 1 ) +ℓ, q=cn(T 2 -T 1 ).
Изменение энтропии ∆s=cn ln (T 2 /T 1 )
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.237.52 (0.007 с.) |

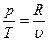 = const, или
= const, или 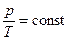 ,
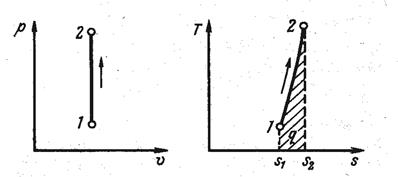
,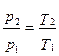 .
.
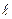 =0, а количество теплоты, подведенной к рабочему телу в процессе 1-2 при c υ=const, определится из соотношения q
=0, а количество теплоты, подведенной к рабочему телу в процессе 1-2 при c υ=const, определится из соотношения q 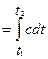 и будет:
и будет: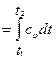 = cυ(t 2 -t 1).
= cυ(t 2 -t 1).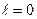 , то по первому закону термодинамики
, то по первому закону термодинамики 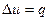 и значит:
и значит: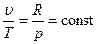 или
или  ,
,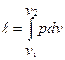 , которое мы рассматривали, следует:
, которое мы рассматривали, следует: .
.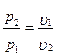 ,
, и вся теплота, подводимая к газу, полностью превращается в работу расширения: q =
и вся теплота, подводимая к газу, полностью превращается в работу расширения: q = 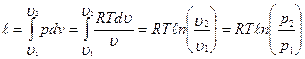
 .
.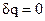

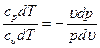 или
или 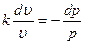 .
.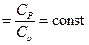 находим:
находим:  ;
; 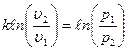 .
. или p1v1k = p2v 2k.
или p1v1k = p2v 2k.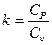 называется показателем адиабаты (т. к. c p= c υ+ R, то k =1+
называется показателем адиабаты (т. к. c p= c υ+ R, то k =1+  ).
). ,
, 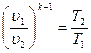 ,
,  .
.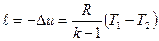 , (7)
, (7) .
.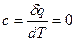 , и ds= 0 (s =const).
, и ds= 0 (s =const).
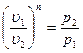 ,
, 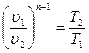 ,
,  .
.



