
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сущность и аналитическое выражение первого закона термодинамикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Первый закон термодинамики представляет собой частный случай всеобщего закона сохранения и превращения энергии применительно к тепловым явлениям. Он утверждает, что энергия не исчезает и не возникает вновь, она лишь переходит из одной формы в другую, причем убыль энергии одного вида дает эквивалентное количество энергии другого вида. Для примера рассмотрим следующий случай: если телу с массой m, объемом V и температурой T, находящемуся под некоторым внешним давлением P, сообщается извне бесконечно малое количество теплоты ∂ Q, то температура тела повышается на dT, а тело расширяется, увеличивая свой объем на dV. Повышение температуры означает увеличение кинетической энергии молекулярного и внутри молекулярного движений частиц тела. Обозначим это приращение внутренней кинетической энергии тела в единицах работы через dК (кгм). Увеличение объема тела обусловливает увеличение расстояние между молекулами, что связанно с производством некоторой внутренней работой так называемой работы дисгрегации (разъединения), идущей на увеличение потенциальной энергии частиц тела, т. е внутренней потенциальной энергии тела, которую обозначим в единицах работы через dР. В результате увеличения объема тела, кроме того, совершает работу преодоления внешнего давления - внешнюю работу, которую обозначим через бL. Таким образом, сочетая все выше сказанное, можно записать уравнение теплового баланса
∂Q= dК+ dP+ бL= (dК+dР)+ ∂L.
Первый член правой части это сумма приращений внутренней кинетической и потенциальной энергии тела, которую назовем внутренней тепловой энергией и обозначим так dK+ dP= dU, тогда получим
∂Q= dU+ ∂L. (4)
Полученное уравнение устанавливает так называемый первый закон термодинамики. Он говорит о том, что теплота, сообщаемая системе, идет на приращение ее внутренней энергии и на совершение внешней работы. Каждый из трех членов этого уравнения, может быть, смотря по обстоятельствам положительным, отрицательным или равным нулю. Если теплота сообщается телу, то ∂Q > 0. Если теплота отводится от тела, то ∂Q < 0. Если внутренняя энергия тела возрастает, то dU > 0. Если она уменьшается, то dU < 0. Если тело расширяется, т. е. совершает работу преодоления внешнего давления, то ∂L > 0.
При сжатии, на которое затрачивается работа извне, ∂L < 0. Теперь рассмотрим некоторые частные случаи: 1. ∂Q= 0, т. е. теплота телу не сообщается и от него не отводится (т.е отсутствует теплообмен с окружающей средой). Такой процесс называется - адиабатным. Из уравнения (4) получаем
∂L= -dU.
это уравнение говорит, что работа расширения, совершаемая системой, равна уменьшению внутренней энергии системы. При адиабатном сжатии (∂ L <0) работа идет на увеличение внутренней энергии системы -∂L=dU. 2. Если ∂L =0, то очевидно, что объем тела не изменяется, т. е. V =соnst, такой процесс носит название изохорного, и для него уравнение выглядит следующим образом:
∂Q= dU,
т. е. сообщаемая телу теплота идет целиком на увеличение его внутренней энергии. 3. Если наконец dU =0 т. е. внутренняя энергия не изменяется (U = =cоnst), то ∂Q= бL,
т. е. сообщаемая телу теплота переходит полностью в эквивалентную ей внешнюю работу. Внутренняя энергия
Внутренней энергией будем называть энергию хаотического движения молекул и атомов, включающую энергию поступательного, вращательного и колебательного движений, как молекулярного, так и внутримолекулярного, а также потенциальную энергию сил взаимодействия между молекулами. Кинетическая энергия молекул зависит от температуры, значение потенциальной энергии зависит от объема. Поэтому внутренняя энергия есть функция состояния тела, и ее изменение (∆U) в термодинамическом процессе не зависит от характера процесса, а определяется только начальным и конечным состоянием тела, т. е.: ∆U= где U 2 - значение внутренней энергии в конечном состоянии, U 1 - в начальном. Так как внутренняя энергия функция состояния, то ее можно представить в виде функции зависимости от двух любых независимых параметров: U=f(p,V); U=f(p,T); U=f(V,T). Внутренняя энергия сложной системы определяется суммой энергий отдельных ее частей, т. е. обладает свойством аддитивности. Величина u=U/m называется удельной, она выражается в Дж/кг. Внутренняя энергия - это свойство самой системы, она характеризует состояние системы.
Работа
Работа в термодинамике, так же как и в механике, определяется произведением действующей на рабочее тело силы на путь ее действия.
Для примера рассмотрим газ, заключенный в цилиндр с поршнем (рис. 4).
Рис. 4
где F - площадь поверхности поршня. Так как Fdy=dV то:
бL= pdV.
При конечном изменении объема L= Выражение справедливо в общем случае и не зависит от формы сосуда, в который помещено рабочее тело и показывает, что работа изменения объема равна произведению давления на приращение объема. Поскольку p величина положительная, то бL и dV всегда имеет одинаковые знаки т. е.: - если dV >0, то бL >0 (при расширении работа положительна - тело само совершает работу); - если же dV <0, то и бL <0, т. е. при сжатии работа отрицательна, это значит, на его сжатие затрачивается работа извне. Единицей измерения работы служит джоуль (Дж). Для исследования равновесных процессов в термодинамике широко используют р-υ диаграмму (рис. 5). Состояние термодинамической системы, как мы уже говорили, определяется двумя параметрами, поэтому на р-υ диаграмме оно будет изображаться точкой.
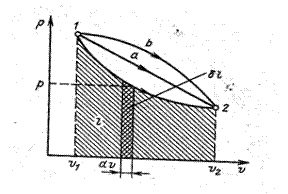 Линия 1-2 есть процесс рас- Линия 1-2 есть процесс рас-
ширения рабочего тела от υ 1 до υ 2. При бесконечно малом изменении объема dυ, пло- щадь заштрихован-ной фигуры pdv=бl, т. е. работа
изменения объема эквивалентна площади под кривой процесса в диаграмме р-υ. Таким образом имея графическое изображение процесса в системе р-υ, мы получаем ясное представление как изменяется давление р и объем υ, расширяется тело или сжимается, и можем определить работу. Изображение процесса в системе р-υ часто называют рабочей диаграммой. Подытоживая можем сказать, что работа зависит от характера термодинамического процесса. Каждому пути перехода системы из состояния 1 в состояние 2 (процесс 1-а-2, 1-b-2, 1-2) соответствует своя работа l1b2>l1a2>l12, т.е. работа не является функцией состояния системы в отличии от р, Т и т. д. Но с другой стороны, что хорошо видно из рис.5, она зависит от пути интегрирования (в процессе 1-2 работа положительная, т. к. dυ >0, а в процессе 2-1 отрицательная, т. к. dυ <0). Работа всегда связана с перемещением макроскопических тел в пространстве, поэтому она характеризует упорядоченную (макрофизическую) форму передачи энергии от одного тела к другому, и является мерой переданной энергии. Работа - это энергическая характеристика процесса механического и теплового взаимодействия системы с окружающей средой. Теплота Помимо макрофизической формы передачи энергии-работы существует также и микрофизическая, т. е. осуществляемая на молекулярном уровне. Мерой количества переданной энергии в этом случае является теплота. Теплота может передаваться либо путем непосредственного контакта (теплопроводностью или конвекцией), либо на расстоянии (излучением), причем процесс теплообмена возможен только при наличии разности температур между телами. Теплота, как и работа, - это энергетическая характеристика процессов механического и теплового взаимодействия системы с окружающей средой.
Энтальпия Энтальпиейбудем называть величину суммы внутренней энергии системы U и произведение давления системы p на величину объема системы V:
I=U+ рV.
Все входящие в уравнение величины является функциями состояния, поэтому и сама энтальпия является функцией состояния и может быть представлена в виде функции двух любых параметров состояния: I=f (р, V), I=f (V, Т), I=f (р, Т). (Раннее мы говорили, теперь вспомним абсолютное давление p, абсолютная температура T, удельный объем v и внутренняя энергия U - все это были параметры состояния, - т.е. всякому состоянию газа присуще вполне определенное значение каждой из этих величин. Теперь к этим величинам добавляется энтальпия.) Часто в расчетах используют значение удельной энтальпии i= I/M, тогда i= u+ pυ, т. е. энтальпия системы, содержащей 1 кг вещества. Так как энтальпия функция состояния, то ее изменение в любом процессе и определяется только начальным и конечным состояниями тела и не зависит от характера процесса: ΔI= Для более ясного понимания энтальпии рассмотрим ее физический смысл. Пусть в цилиндре под поршнем с грузом находится газ (рис. 6).
 Давление газа уравновешивается грузом весом G= pF. Полная энергия Е расширенной системы (газ и поршень с грузом) будет равна сумме внутренней энергии газа U и потенциальной энергии поршня с грузом, равной рFу= pV, исходя Давление газа уравновешивается грузом весом G= pF. Полная энергия Е расширенной системы (газ и поршень с грузом) будет равна сумме внутренней энергии газа U и потенциальной энергии поршня с грузом, равной рFу= pV, исходя
из этого запишем:
Е= U+ pV = I. Член pV численно равен работе, которую нужно совершить, чтобы ввести объем V газа из вакуума в пространство с давлением p. То есть энтальпиялюбой системы представляет собой сумму внутренней энергии системы и потенциальной энергии источника внешнего давления. Очень часто приходится решать задачи, в которых подвод тепла к системе осуществляется при постоянном давлении (изобарный процесс) dp =0, тогда теплота, подведенная к системе, расходуется только на изменение энтальпии: qр= i2- i1.
(т. к. бq= du+ pdυ= du+ d(pυ)- υdp= d(u+pυ)- υdp, бq = di-υdp, т. е. при p= const бqp = di). Энтропия При любом равновесном процессе перехода тела из состояния 1 в состояние 2 величина интеграла ds= Подобно других выражений для произвольной массы газа S=Мs (Дж/К). Как и любые другие функции состояния, энтропия может быть представлена в виде функции любых двух параметров состояния: s= f(p,υ), s= f(p,T), s= f(υ,T). Понятие энтропии позволяет ввести чрезвычайно удобную для термодинамических расчетов T-s диаграмму, на которой (как и на p - v диаграмме) состояние термодинамической системой изображается точкой, а равновесный термодинамический процесс линией (рис. 6).
Т-s -диаграмма выглядит следующим образом (рис. 7):
Рис. 7
Из уравнения (5) следует, что
Очевидно, что в Т-s - диаграмме элементарная теплота процесса Из (6) видно, что ds и Например, при нагревании тела ( Подставляя уравнение(5) в уравнение первого закона термодинамики получаем термодинамические тождества для равновесных процессов: δq= Тds=du+ pdυ; δq= Tds= di-υdp.
Второй закон термодинамики
Второй закон термодинамики определяет направление, в котором протекают процессы, устанавливают условия преобразования тепловой энергии в механическую, а также определяет максимальное значение работы, которая может быть произведена тепловым двигателем. Согласно первому закону термодинамики взаимное превращение тепловой и механической энергии осуществляется в строго эквивалентных количествах. Но, несмотря на эквивалентность теплоты и работы, процессы их взаимного превращения неравнозначны. Опыт показывает, что механическая энергия может быть полностью превращена в теплоту (например, путем трения). Однако теплоту полностью превратить в механическую энергию нельзя. Всяческие попытки осуществить такой процесс не увенчались успехом. Это связано с существованием фундаментального закона природы, называемого вторым законом термодинамики.
лодный источник теплоты. Горячими источниками служат химические реакции сжигания топлива. Отметим, что рабочее тело в машине совершает замкнутый круговой процесс – цикл. Холодными является окружающая среда (атмосфера). Рабочим телом является газ. Рассмотрим, как осуществляется работа двигателя по p-v - диаграмме (рис. 9).
Эта работа должна быть меньше работы расширения. Поэтому кривая сжатая должна лежать ниже кривой расширения. Затраченная в процессе сжатия 2А1 работа изображается площадью 21А1'2'.
В результате цикла совершается полезная работа l ц эквивалентная площади 1В2А1, ограниченная контуром цикла. Проведем две адиабаты, касательные к контуру цикла, тогда он разобьется на два участка: А1В и В2А. На участке А1В происходит подвод теплоты q 1, на участке В2А отвод теплоты q 2. В точках А и В, лежащих на адиабатах, нет ни отвода ни подвода теплоты, в этих точках поток теплоты меняет знак. Суммируя все вышесказанное, можно сделать следующее заключение: для непрерывной работы двигателя необходим циклический процесс, в котором к рабочему телу от горячего источника подводится теплота q 1 и отводится от него к холодному телу теплота q 2. В T-s -диаграмме этот цикл будет выглядеть следующим образом (рис. 10).
Рис. 10
Внутренняя энергия du – функция состояния рабочего тела, поэтому при возвращении рабочего тела в исходное состояние оно приобретает свое начальное значение и поэтому Значит q ц= l ц - это теплота, полезно использованная в цикле, и равна она разности теплоты q 1- q 2 (в T-s -диаграмме q ц эквивалентна площади, ограниченной контуром А1В2А). Основным показателем любого двигателя является коэффициент полезного действия. Термическим коэффициентом полезного действия (КПД) будем называть отношение работы, произведённой за цикл, к количеству теплоты, отнятой от теплоисточника (подведённой за этот цикл от горячего источника):
КПД оценивает степень совершенства теплового двигателя. Чем он выше, тем большая часть теплоты превращается в работу. Для закрепления второго закона сформулируем его ещё раз таким образом: невозможно построить такую машину, которая бы превращала в работу всю теплоту, отнятую от теплового источника, без передачи части этой теплоты холодильнику.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 786; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.233.198 (0.014 с.) |

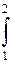 dU= U2-U1,
dU= U2-U1,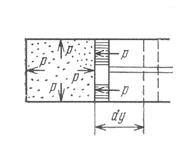 Если газу сообщить некоторое количество теплоты, то он будет расширяться, совершая работу против внешнего давления P, оказываемого на него поршнем, перемещая поршень на величину dy, т. е. работа
Если газу сообщить некоторое количество теплоты, то он будет расширяться, совершая работу против внешнего давления P, оказываемого на него поршнем, перемещая поршень на величину dy, т. е. работа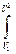 рdV.
рdV.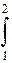 dI= I1-I2.
dI= I1-I2. не зависит от самого процесса, а зависит только от начального и конечного состояния тела. Это значит, что стоящая под знаком интеграла величина является полным дифференциалом. Это выражение называется энтропией. Для 1 кг газа (Дж/кг · К).
не зависит от самого процесса, а зависит только от начального и конечного состояния тела. Это значит, что стоящая под знаком интеграла величина является полным дифференциалом. Это выражение называется энтропией. Для 1 кг газа (Дж/кг · К).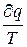 . (5)
. (5)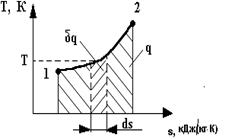 Так как энтропия – есть функция состояния, то уравнением можно пользоваться вне зависимости от пути интегрирования перехода рабочего тела между состояниями 1 и 2.
Так как энтропия – есть функция состояния, то уравнением можно пользоваться вне зависимости от пути интегрирования перехода рабочего тела между состояниями 1 и 2. ; (6)
; (6)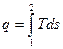 .
.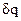 изображается площадкой с высотой Т и основанием ds, а площадь, ограниченная линией процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса.
изображается площадкой с высотой Т и основанием ds, а площадь, ограниченная линией процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса.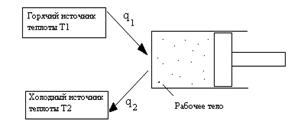 Для того чтобы выяснить его сущность, рассмотрим принципиальную схему теплового двигателя (рис. 8).
Для того чтобы выяснить его сущность, рассмотрим принципиальную схему теплового двигателя (рис. 8).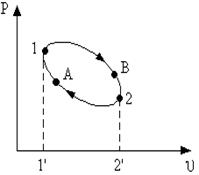 Расширяясь, по линии 1В2 рабочее тело совершает работу, равную площади 1В22’1’. В непрерывнодействующей машине этот процесс должен повторяться, для чего необходимо возвращать рабочее тело в исходное состояние - производить работу сжатия.
Расширяясь, по линии 1В2 рабочее тело совершает работу, равную площади 1В22’1’. В непрерывнодействующей машине этот процесс должен повторяться, для чего необходимо возвращать рабочее тело в исходное состояние - производить работу сжатия.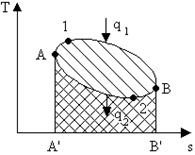 Количество подводимой теплоты q 1 на диаграмме соответствует площади А1ВВ'A’, отводимой q 2 площади В2АА'B'.
Количество подводимой теплоты q 1 на диаграмме соответствует площади А1ВВ'A’, отводимой q 2 площади В2АА'B'.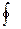 δq=
δq= 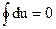 .
.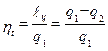 .
.


