
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приравняв правые части двух уравнений, получимСодержание книги
Поиск на нашем сайте
Правая и левая части этого уравнения имеют разные знаки, следовательно, увеличение скорости течения в канале ds > 0 возможно лишь при уменьшении давления в нем (dp < 0). И, наоборот, торможение потока dc < 0 сопровождается увеличением давления dp > 0. Каналы, в которых происходит разгон газа, называются соплами. Каналы, предназначенные для торможения потока, называются диффузорами. Так как длина сопла и диффузора невелика, а скорость течения среды в них достаточно высока, то можно считать, что теплообмена между стенками канала и средой нет(q внеш = 0), и тогда уравнение первого закона термодинамики для потока примет вид
То есть ускорение адиабатного потока происходит за счет уменьшения энтальпии, а торможение потока вызывает увеличение энтальпии. Истечение из суживающегося сопла Расчет сопла сводится к определению скорости на выходе, нахождению F и правильному выбору его формы. Рассмотрим процесс равновесного (без трения) адиабатного истечения газа через сопло из резервуара. Скорость газа на входе c 1, давление на выходе p 2 = p окр ср.. Из уравнения (8) запишем чему, равна скорость истечения газа
Если принять площадь входного сопла достаточно большой, то с 1 = 0 и с 2 представлено ниже
где Δi0 = i 1 – i 2 = u 1 – u 2 + (p1v1 – p 2 v 2) – располагаемый адиабатный перепад. Для идеального газа в адиабатном процессе u 1 – u 2 = ℓ мы вычисляем по формуле (7), (
Тогда скорость
Так как процесс адиабатный, то ( Массовый расход газа Массовый расход газа m, кг/с, через сопло
где F – площадь выходного сечения сопла, м2. Если подставить в эту формулу значение с2 из формулы (10), то получим
Из выражения (12) получим, что массовый секундный расход идеального газа при истечении из большого резервуара зависит от площади выходного сечения сопла F, свойств k, начальных параметров газа (P 1, V 1) и степени его расширения (то есть давления P 2 газа на выходе). По уравнению (12) построена кривая OK1(рис.26).
Сравнение описанной зависимости с экспериментальными данными показало, что для β кр < P 2/ P 1 < 1 результаты совпадают, а для 0 < P 2/ P 1 < β кр – расходятся. Здесь действительный массовый расход остается постоянным (прямая KD). Объяснение этому было дано Сен-Венаном в гипотезе о том, что в суживающемся сопле невозможно получить давление газа ниже некоторого критического значения p кр, соответствующего максимальному расходу газа через сопло. Как бы мы ни понижали давление P 2 среды, куда происходит истечение, давление на выходе из сопла остается постоянным и равным p кр. Для отыскания максимума функции m уравнения (12) при p 1 = const, соответствующего значению β кр, возьмем первую производную от выражения в квадратных скобках и приравняем ее нулю
Отсюда получим
то есть отношение критического давления на выходе P 2 = P кр к давлению перед соплом P 1 есть величина постоянная, зависящая только от показателя адиабаты, то есть от природы рабочего тела. Мы уже знаем: для одноатомного газа k = 1,66, для двухатомного k = 1,4, для трехатомного газа и перегретого водяного пара k = 1,3. Тогда для одноатомного βкр = 0,49; двухатомного βкр = 0,528; трехатомного βкр = 0,546. Таким образом, изменение βкр невелико и для оценочных расчетов можно принять βкр = 0,5. Критическую скорость можно определить из уравнения (10), подставив в него вместо отношения давлений P 2/ P 1 значение βкр
Величина критической скорости определяется физическими свойствами и начальными параметрами газа. Из уравнения адиабаты следует
Заменяя отношение давлений на βкр, согласно (13) получим
Подставляя значение P 1 из (16) и P 1 из уравнения (15) в формулу для определения c кр (14), получим
В физике выражение
|
|||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.136.222 (0.009 с.) |


 . (8)
. (8) .
. , (9)
, (9) ), поэтому можем записать
), поэтому можем записать .
. .
. ) – это мы получили в главе «термодинамический и газовый процессы».
) – это мы получили в главе «термодинамический и газовый процессы».  (10)
(10) , (11)
, (11) . (12)
. (12)
 .
. . (13)
. (13)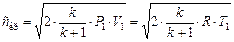 . (14)
. (14) . (15)
. (15) . (16)
. (16) . (17)
. (17) = a есть скорость распространения звука в среде. Таким образом, критическая скорость газа при истечении равна местной скорости звука в выходном сечении сопла.
= a есть скорость распространения звука в среде. Таким образом, критическая скорость газа при истечении равна местной скорости звука в выходном сечении сопла.


