
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет процесса истечения с помощью i-s – диаграммСодержание книги
Поиск на нашем сайте
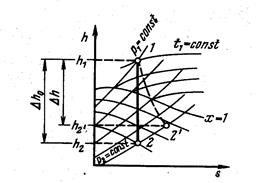
Водяной пар не является идеальным газом, и поэтому расчет его истечения лучше выполнять не по аналитическим формулам, а с помощью i,s – диаграммы водяного пара (рис. 27).
Рис. 27 протекать при постоянной энтропии и изображается на i,s – диаграмме вертикальной прямой – 1-2.
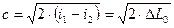 , где i 1 – определяется на пересечении линий P 1 и t 1, а i 2 – находится на пересечении линии 12 с изобарой P 2. , где i 1 – определяется на пересечении линий P 1 и t 1, а i 2 – находится на пересечении линии 12 с изобарой P 2.
Если подставим c 2 и i 2 в эту формулу в кДж/кг (как на i,s - диаграмме), то скорость получим в м/с:
Для определения критической скорости или критического давления по i, s –диаграмме воспользуемся методом последовательных приближений, который состоит в следующем: задавшись в первом приближении значением k = 1,3 соотношения для нахождения β кр (13) находим P кр. Затем по известным P кр и S кр = S 1 определим удельный объем V кр по i, s –диаграмме. Далее из соотношения для адиабатного процесса:
найдем новое значение k (второе приближение), по которому снова определим P кр и т. д. Вычисление заканчиваем, когда значение Р кр, по которому определяется k, совпадет с его значением, вычисленным по формуле (13) для βкр. В реальных условиях вследствие трения потока о стенки канала и внутреннего трения между струйками процесс истечения оказывается необратимым, то есть при течении газа выделяется теплота трения и поэтому энергия рабочего тела возрастает. На i, s -диаграмме это будет выглядеть (рис. 28).
 на выходе из сопла получается естественно меньше, чем при отсутствии трения. Потеря кинетической энергии в сопле и располагаемому теплопадению называется коэффициентом потери энергии в сопле ξс на выходе из сопла получается естественно меньше, чем при отсутствии трения. Потеря кинетической энергии в сопле и располагаемому теплопадению называется коэффициентом потери энергии в сопле ξс
Выразив из этого выражения действительное теплопадение через располагаемое
и подставив его в формулу (11), получим формулу для подсчета действительной скорости адиабатного необратимого истечения
где φс – скоростной коэффициент сопла. Обычно φс = 0,95 – 0,98.
Смешение газовых потоков Если n потоков с различными параметрами соединяются в один поток, то при адиабатном течении газов без совершения внешней работы полная энергия потока газовой смеси равна сумме полных энергий потоков, составляющих смесь:
Для большинства технических задач по причине малых скоростей течения можно пренебречь кинетическими энергиями по сравнению со значениями энтальпий соответствующих потоков:
или Это уравнение справедливо для потоков идеальных и реальных газов, паров и жидкостей. Для идеального газа i = c p T, и значит уравнение примет вид
откуда можно найти температуру Т cм. Объем смеси идеальных газов определяется из уравнения состояния.
Сопло Лаваля
Условие неразрывности течения в потоках заключается в одинаковости массового расхода m рабочего тела в любом сечении
Возьмем дифференциал от левой и правой частей этого уравнения при условии m = const
Разделив (19) на (18), получим
При адиабатном равновесном расширении идеальных газов связь между P и v
Применимо и для процесса истечения водяного пара k = 1,3. После дифференцирования уравнения адиабаты получим
Разделив уравнение cdc=-v dp на pv, найдем
Подставляем в (20) вместо
Если рассмотреть движение газа через сопло, которое предназначено для увеличения скорости потока, то dc > 0 и знак у dF определяется отношением скорости потока с к скорости звука в данном сечении. Если скорость потока мала с/а < 1, то скобка в правой части (23) отрицательна и dF < 0, то есть сопло суживается. Если же с / а > 1, то dF > 0, т. е. Сопло должно расширяться. Впервые профиль для получения сверхзвуковых скоростей за соплом получил шведский инженер Лаваль. Его сопло состоит из двух частей: суживающийся, где с < а, и расширяющейся, где с > а (рис. 29).
Рис. 30
 < βкр скорость истечения меньше скорости звука в вытекающей среде. Внутри сопла скорость потока также везде меньше скорости звука. Следовательно, сопло должно быть суживающимся по всей длине. < βкр скорость истечения меньше скорости звука в вытекающей среде. Внутри сопла скорость потока также везде меньше скорости звука. Следовательно, сопло должно быть суживающимся по всей длине.
При более низком давлении за соплом можно получить режим, когда скорость на выходе равна скорости звука в вытекающей среде. Внутри сопло суживающееся и только в выходном сечении dF = 0.
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 465; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.242.56 (0.011 с.) |

 Пусть пар с начальными параметрами P 1, T 1 вытекает в среду с давлением p 2. Если пренебречь потерями энергии на трение и теплоотдачей к стенкам сопла, то процесс истечения будет
Пусть пар с начальными параметрами P 1, T 1 вытекает в среду с давлением p 2. Если пренебречь потерями энергии на трение и теплоотдачей к стенкам сопла, то процесс истечения будет .
.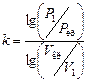 .
. При этом же перепаде давлений P 1 – P 2 разность энтальпий
При этом же перепаде давлений P 1 – P 2 разность энтальпий .
.
 ,
, .
.
 .
. ,
, . (18)
. (18) . (19)
. (19) . (20)
. (20) ,
, . (21)
. (21) . (22)
. (22) его выражение из (21) с учетом (22) получим
его выражение из (21) с учетом (22) получим . (23)
. (23)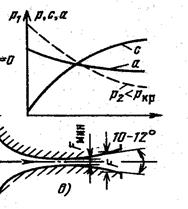 При истечении газа из такого сопла в среду с давлением меньше критического, в самом узком сечении сопла устанавливаются критические давление и скорость. В расширяющейся насадке происходит дальнейшее увеличение скорости и соответственно падение давления истекающего газа до давления внешней среды.
При истечении газа из такого сопла в среду с давлением меньше критического, в самом узком сечении сопла устанавливаются критические давление и скорость. В расширяющейся насадке происходит дальнейшее увеличение скорости и соответственно падение давления истекающего газа до давления внешней среды.



