
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоемкость и энтальпия влажного воздухаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теплоемкость влажного воздуха при постоянном давлении (изобарную) ср обычно относят к 1 кг сухого воздуха (или к (1+ d) кг. влажного). Она равна сумме теплоемкостей 1 кг сухого воздуха и d кг пара:
с р =с рв +dс рп.
В приближенных термодинамических расчетах в небольшом диапазоне температур принимают удельную изобарную теплоемкость воздуха c рв≈1 кДж/(кг·К), удельную изобарную теплоемкость водяного пара c рп≈2. Тогда c р =1+2d.
Энтальпия влажного воздуха определяется как энтальпия газовой смеси, состоящей из 1 кг сухого воздуха и d кг водяного пара: i=i в +di п,
где энтальпии 1 кг сухого воздуха
i в =с рв t= 1 t;
энтальпия 1 кг пара
i п = 2500 + 2 t,
где 2500 кДж/кг -теплота испарения воды при 0°С. Тогда получаем: i=t +( 2500 + 2 t)d. I-d - диаграмма влажного воздуха С помощью I-d диаграммы решаются практические задачи в области кондиционирования, сушки, вентиляции, отопления. Выглядит диаграмма, предложенная Л.К. Рамзиным, следующим образом (рис. 50) В диаграмме энтальпия (1-М) кг влажного воздуха (ось ординат) представлена как функция абсолютной влажности и, г/кг, (ось абсцисс). Для удобства пользования I-d -диаграмма построена в косоугольных координатах: ось абсцисс направлена под углом 135° к оси ординат. На рис. 50 диаграмме наклонная ось не показана, вместо нее из начала координат проведена горизонтальная прямая, на которой даны значения влагосодержания. Таким образом, линии d =соnst — это вертикальные прямые, а линии I =соnst — наклонные прямые. Так как энтальпия является линейной функцией t и d, то изотермы изображаются на диаграмме прямыми линиями. Кроме того, на диаграмме нанесены кривые φ=соnst. Кривая φ=100 % - кривая насыщения. Она является своего рода пограничной кривой, разделяющей область ненасыщенных состояний (вверху) и область тумана (внизу), в котором часть влаги находится в виде пара, а часть- в жидком или твердом виде (снег, ледяной туман).
рис.50 Любая точка в I-d диаграмме обозначает вполне определенное физическое состояние воздуха, а изменение этого состояния изображается линией процесса. Так, например, в процессе нагрева воздуха в калорифере (воздухонагревателе) влагосодержание воздуха не изменяется (d =соnst), поэтому он изображается в I-d диаграмме вертикальной прямой (линия 1-4).
В процессе охлаждения воздуха в воздухоохладителе при d =соnst (линия 1-2) повышается его относительное влагосодержание, и при определенной температуре t 2, равной температуре точки росы, воздух становится насыщенным (φ =100 %). При дальнейшем охлаждении воздуха будет происходить конденсация водяных паров из него и соответственно осушение воздуха (линия 2-3). Количество сконденсированного воздуха определяется конечной температурой и выражается разностью влагосодержаний d 1- d 3. Воздух может охлаждаться и за счет непосредственного испарения в него воды, имеющей более низкую температуру. Если теплота, необходимая для испарения воды, берется только из окружающего воздуха, то влагосодержание его будет увеличиваться, а температура понижаться. Такой процесс адиабатного охлаждения влажного воздуха пойдет по линии 1-5при I =соnst, а пределом охлаждения будет адиабатная температура мокрого термометра.
Теория теплообмена Передача теплоты от одного тела к другому играет большую роль в теплотехнике. Многие элементы основного и вспомогательного оборудования электростанций и технологического оборудования различных отраслей промышленности - это различные виды теплообменных аппаратов. При построении этих аппаратов стремятся к тому, чтобы передать заданное количество тепла от одного тела к другому при минимальных размерах аппарата. Необходимо, следовательно, обеспечить как можно большую скорость передачи теплоты. В других случаях нужно, напротив, уменьшить интенсивность теплообмена, например, для уменьшения непроизводительных потерь теплоты в окружающую среду. Во всех этих случаях необходимо знание законов передачи и распределения теплоты, факторов, влияющих на увеличение или уменьшение интенсивности теплообмена, а также методов расчета теплообмена и теплообменных аппаратов. Наука, изучающая эти вопросы, называется теорией теплопередачи (теплообмена). В теории теплообмена изучаются закономерности переноса теплоты из одной области пространства в другую. Процессы переноса теплоты представляют собой процессы обмена внутренней энергией между элементами рассматриваемой системы в форме теплоты.
Виды теплообмена. Теплопроводность - молекулярный перенос теплоты в сплошной среде, обусловленный наличием градиента температуры. Конвективный теплообмен - перенос теплоты, обусловленный перемещением макроскопических элементов среды в пространстве. Теплоотдача – конвективный теплообмен между движущейся средой и поверхностью её раздела с другой средой (твёрдым телом, жидкостью или газом). Лучистый теплообмен – теплообмен, обусловленный превращением внутренней энергии вещества в энергию электромагнитных волн, распространением их в пространстве и поглощением энергии этих волн веществом. В реальных условиях все три вида теплообмена, как правило, протекают одновременно, например, в процессе теплопередачи от одной жидкой или газообразной среды к другой, через разделяющую их стенку. Количественные характеристики переноса теплоты. Интенсивность переноса теплоты характеризуется плотностью теплового потока, то есть количеством теплоты, передаваемой в единицу времени через единичную площадь поверхности (обычно обозначается q, Вт/м2). Количество теплоты, передаваемой в единицу времени через произвольную поверхность F, называют мощностью теплового потока или просто тепловым потоком (обозначают Q, Дж/с = =Вт). Количество теплоты, передаваемое за произвольный промежуток времени Согласно изложенному запишем соотношения между рассмотренными величинами q = Теплопроводность Аналитическая теория теплопроводности применима только к сплошной среде. При расчёте процессов теплопроводности не учитывается дискретное строение тел, принимается, что тела гомогенны и изотропны, а размеры их велики по сравнению с расстоянием между молекулами. Основной задачей теплопроводности является определение температурного поля в теле. Температурное поле- совокупность значений температуры во всех точках тела (или пространства) в некоторый фиксированный момент времени. Температурное поле может быть нестационарным и стационарным. В первом случаи считается, что поле изменяется во времени, во втором нет. В соответствии с этим и процесс теплопроводности считается стационарным или нестационарным. Функция, определяющая температурное поле, в рассматриваемом поле в общем виде записывается так:
t = f (x, y, z, где x, y, z - координаты точки; 1) Нестационарное трёхмерное t = f (x, y, z, 2) Стационарное двухмерное t = f (x, y); 3) Стационарное одномерное t = f (x); Пример одномерной задачи - перенос теплоты в стенке, имеющей длину и ширину бесконечно большие по сравнению с толщиной. Поверхность, во всех точках которой температура одинакова, называется изотермической. Такие поверхности не пересекаются между собой. Они могут быть замкнутыми (замыкаются на себя) или кончаются на границах тела. Рассмотрим две близкие изотермные поверхности с температурами t и t +
Рис. 51 не обнаружим. Если перемещаться вдоль направления S, то будет наблюдаться изменение температуры. Наибольшую разность температур на единицу длины будем наблюдать в направлении нормали к изотермической поверхности.
Градиент температуры - вектор, направленный по нормали к изотермной поверхности в сторону возрастания температуры и численно равный частной производной от температуры по этому направлению: grad grad где Проекции вектора grad t на координатные оси x, y, z равны: (grad ( (grad t)z = Тепловой поток – количество теплоты, переданное через произвольную поверхность в единицу времени Тепловой поток, отнесённый к единице площади поверхности, называется плотностью теплового потока. Она может быть местной (локальной) и средней по поверхности; характеризует интенсивность переноса теплоты и является вектором, направление которого совпадает с направлением падения температуры, (Вт/м2 ). q = Основной закон теплопроводности (закон Фурье). Необходимым условием для распространения теплоты является неравномерность распределения температуры в рассматриваемом теле. Таким образом, для передачи теплоты теплопроводностью необходимо условие неравенства нулю температурного градиента в различных точках тела.Опытным путём установлено, что плотность теплового потока, передаваемого теплопроводностью, прямо пропорциональна градиенту температуры, (Вт/м2).
где Знак минус указывает на то, что вектор Данное уравнение является математическим выражением закона теплопроводности Фурье, а значение Величина Коэффициент теплопроводности при 20
На рис. 52 показана зависимость коэффициента теплопроводности от температуры: 1 – воздух; 2 – минеральная вата (ρ=150 кг/м³); 3 – минеральная вата (ρ=400 кг/м³); 4 – сухой пористый красный кирпич; 5 – вода; 6 – железо (99,9 %); 7 – латунь(67 % меди, 33 % цинка); 8 – медь (99,9 %); 9 – серебро (99,9 %). Из сказанного следует, что для определения количества теплоты, проходящей через какую-либо поверхность твёрдого тела, необходимо знать температурное поле внутри этого тела. Нахождение температурного поля и является главной задачей аналитической теории теплопроводности.
Как было отмечено, коэффициент теплопроводности является физическим параметром вещества и в общем случае зависит от температуры, давления и рода вещества. В большинстве случаев он определяется экспериментально с помощью различных методов, большинство из которых основано на измерении теплового потока и градиента температур в исследуемом веществе. Коэффициент теплопроводности при этом определяется из соотношения, λ, Вт/м·К,
из которого следует, что коэффициент теплопроводности численно равен количеству теплоты, которое проходит в единицу времени через единицу изотермической поверхности при температурном градиенте, равном единице. Поскольку тела могут иметь различную температуру, а при наличии теплообмена и в самом теле температура будет распределена неравномерно, то, в первую очередь, важно знать зависимость коэффициента теплопроводности от температуры. Опыты показывают, что для многих материалов с достаточной для практики точностью эту зависимость можно принять линейной:
где
Согласно кинетической теории перенос теплоты теплопроводностью в газах при обычных давлениях и температурах определяется переносом кинетической энергии молекулярного движения в результате хаотического движения и столкновения отдельных молекул газа. При этом коэффициент теплопроводности определяется соотношением:
где
С увеличением давления в равной мере увеличивается плотность Поэтому Средняя скорость перемещения молекул газа зависит от температуры:
где
Т - температура, Поскольку теплоёмкость газа растёт с повышением температуры, коэффициент также повышается: 0,006 Среди газов резко выделяется водород и гелий. У них
Коэффициенты теплопроводности водного пара и других реальных газов, существенно отличающихся от идеальных, сильно зависят от давления. Для газовых смесей коэффициент теплопроводности не может быть определён по закону аддитивности и его нужно определять опытным путём. Механизм распространения теплоты в капельных жидкостях можно представить как перенос энергии путём нестройных упругих колебаний. Для большинства жидкостей эта теория нашла хорошее подтверждение, и на основании её была получена формула для коэффициента теплопроводности:
где
Опыт показывает, что для большинства жидкостей с повышением температуры коэффициент теплопроводности убывает; исключения составляют вода и глицерин. Коэффициент 0,07 При повышении давления коэффициент теплопроводности жидкостей возрастают. В металлах основным передатчиком теплоты являются свободные электроны, которые можно уподобить идеальному одноатомному газу. Вследствие движения свободных электронов происходит выравнивание температуры во всех точках нагревающегося или охлаждающегося металла. Свободные электроны движутся как из областей более нагретых в области, менее нагретые, так и в обратном направлении. В первом случаи они отдают энергию атомам, во втором отбирают её. Так как носителем тепловой энергии является электрон, то коэффициенты теплопроводности и электропроводности пропорциональны друг другу. При повышении температуры вследствие усиления тепловых неоднородностей рассеивание электронов увеличивается. Это влечёт за собой уменьшение коэффициентов теплопроводности и электропроводности чистых металлов. При наличии разного рода примесей В отличие от чистых металлов В диэлектриках с повышением температуры коэффициент теплопроводности обычно увеличивается. Как правило, для материалов с большей плотностью Простейшей и очень распространённой задачей, решаемой теорией теплообмена, является определение плотности теплового потока, передаваемого через плоскую стенку, толщина которой
В стационарных условиях, когда энергия не расходуется на нагрев, плотность теплового потока
средней между температурами поверхностей стенки. В этом случаи зависимость температуры t от координаты x линейна (рис. 53):
Получим зависимость для расчёта плотности теплового потока:
или
Полученная формула имеет широкое распространение в тепловых расчётах. Отношение λF/δ называется тепловой проводимостью стенки, а обратная величина Пользуясь понятием термического сопротивления, формулу для расчёта теплового потока можно представить
аналогично закону Ома в электротехнике (величина электрического тока равна разности потенциалов, делённой на электрическое сопротивление проводника, по которому течёт ток).
Для расчёта теплового потока через стенку, состоящую из нескольких плотно прилегающих друг к другу слоёв разнородных материалов (многослойная стенка) пользуются формулой, приведенной выше. Термическое сопротивление такой стенки равно сумме термических сопротивлений отдельных слоёв: В формулу нужно подставлять разность температур в тех точках (поверхностях), между которыми включены все суммируемые термические сопротивления то есть
Распределение температур в пределах каждого слоя – линейное, однако в различных слоях крутизна температурной зависимости различна, поскольку:
Плотность теплового потока проходящего через все слои в стационарном режиме одинакова, а коэффициент теплопроводности слоёв различен, следовательно, более резко температура меняется в слоях с меньшей теплопроводностью.
Рассчитав тепловой поток через многослойную стенку, можно определить падение температуры в каждом слое по соотношению
 за любым слоем за любым слоем  : :
Часто теплоносители движутся по трубам, и требуется рассчитать тепловой поток, передаваемый через цилиндрическую стенку трубы (рис. 55). Эта задача также одномерная, если её рассматривать в цилиндрических координатах. Температура изменяется только вдоль радиуса (по координате r), а по длине трубы и по её периметру остаётся неизменной. В этом случае
или
Интегрировать удобнее последнее уравнение, так как тепловой поток не меняется по толщине стенки, а Разделим переменные:
У внутренней поверхности, где кривизна стенки больше, температура меняется резче, чем у наружной. Интегрирование уравнения
Термическое сопротивление
Эта формула достаточно сложная и причём при значениях Для определения теплового потока через многослойную цилиндрическую стенку следует, как и для многослойной плоской стенки, просуммировать термические сопротивления отдельных слоёв:
При постоянных температурах
Разделив переменные и проинтегрировав по
получим формулу для теплового потока через шаровую стенку:
В отличие от цилиндра и пластины тепловая изоляция бесконечной толщины
Конвективный теплообмен (теплоотдача) Обычно жидкие и газообразные теплоносители нагреваются или охлаждаются при соприкосновениями с поверхностями твёрдых тел. Процесс теплообмена между поверхностью твёрдого тела и жидкостью называется теплоотдачей, а поверхность тела, через которую переносится теплота,- поверхностью теплообмена. Мы будем здесь называть жидкостью как капельные жидкости, так и газы, причём ограничимся случаем движением газов со скоростями, небольшими по сравнению со скоростями звука и, следовательно, малым относительным изменением давления, что позволяет пренебрегать сжимаемостью газов. По закону Ньютона–Рихмана тепловой поток в процессе теплоотдачи пропорционален площади поверхности теплообмена F и разности температур поверхности
В процессе теплоотдачи, независимо от теплового потока Q, его значение принято считать положительным, поэтому разность температур берут по абсолютной величине. Коэффициент пропорциональности
Коэффициент теплоотдачи может быть различным в разных точках поверхности теплообмена, в этом случаи вводят понятие местного коэффициента, а также для упрощения тепловых расчётов часто пользуются средним по поверхности коэффициентом теплоотдачи В зависимости от причины, вызывающей движение, различают вынужденное и свободное движение. Вынужденное движение жидкости вызывается работой насоса, ветра, дымовой трубы или другого устройства, причём между входом или выходом из канала, по которому движется жидкость, устанавливается определённая разность давлений. Движущая сила в данном случае непосредственно связана с этим перепадом давления. Свободное движение (естественная конвекция) может происходить и при отсутствии перепада давлений и обуславливается различием удельного веса жидкости в разных точках рассматриваемого объёма. Например, при нагревании воздуха у одной стенки от батареи его плотность и удельный вес уменьшаются, он поднимается вверх и замещается холодным поступающим снизу. Здесь движение связано с разностью температур. То есть естественная конвекция возникает только при теплообмене за счёт теплового расширения нагретой около теплоотдающей поверхности жидкости. Интенсивность теплового расширения характеризуется температурным коэффициентом объёмного расширения:
где Для газов, которые в большинстве случаев можно считать идеальными, то есть Для капельных жидкостей он меньше чем для газов, а иногда может принимать нулевое или отрицательное значения. Например, для воды при t= 4 °C Для небольших диапазонов температур, а значит и удельных объёмов можно записать
где индекс “ ж ” для холодной жидкости; без индекса параметры прогретой жидкости. Теория подобия – это учение о подобных явлениях. Условием подобия полей физических величин является пропорциональность значений этих величин в сходственных точках. У подобных явлений подобны поля всех физических величин, характеризующих эти явления, то есть
где Так, в подобных процессах теплоотдачи от пластин к продольно омывающим их потокам. Этому условию должны удовлетворять:
Для нахождения условий подобия математическое описание процесса приводят к безразмерному виду. Основная трудность, возникающая при экспериментальном исследовании конвективного теплообмена, заключается в том, что коэффициент теплоотдачи зависит от многих параметров. Например, средний по поверхности коэффициент теплоотдачи от продольно омываемой пластины зависит от длины пластины
Вт/(м2 ·К)=(м, м/с, Вт/м·К, Дж/м·К, кг/м3, м 2 /с) Если проводить эксперименты, изменяя m раз каждый из 6 параметров, влияющих на теплообмен, то суммарное число экспериментов будет N=m6. Теория показывает, что число параметров зависит от выбора единицы измерения. Наименьшее число параметров получится, если единицы измерения будут связаны с самой решаемо
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 7828; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.192.89 (0.011 с.) |


 через произвольную поверхность F, будем обозначать Q
через произвольную поверхность F, будем обозначать Q  .
. =
=  .
. t /
t / 
 0.
0. t (рис. 51).
t (рис. 51). Перемещаясь из точки О, можно обнаружить, что интенсивность изменения температуры по различным направлениям неодинакова. Если перемещаться по изотермной поверхности, то изменения температуры
Перемещаясь из точки О, можно обнаружить, что интенсивность изменения температуры по различным направлениям неодинакова. Если перемещаться по изотермной поверхности, то изменения температуры =
= 
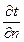 (град/м):
(град/м): =
= 
 ;
;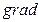

 ;
;
 .
. ,
,  .
. .
.
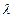 - коэффициент-теплопроводности, определяется опытным путём и зависит от агрегатного состояния вещества, температуры, давления, структуры, плотности и влажности.
- коэффициент-теплопроводности, определяется опытным путём и зависит от агрегатного состояния вещества, температуры, давления, структуры, плотности и влажности. и
и  t имеют противоположные направления.
t имеют противоположные направления. .
.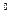 С (Вт/м·К)
С (Вт/м·К)
 ,
, ,
, - значение коэффициента теплопроводности при температуре
- значение коэффициента теплопроводности при температуре  ;
; - постоянная, определяемая опытным путём.
- постоянная, определяемая опытным путём. ,
, - средняя скорость перемещения молекул газа;
- средняя скорость перемещения молекул газа; - средняя длина свободного пробега молекул газа между соударениями;
- средняя длина свободного пробега молекул газа между соударениями; - удельная теплоёмкость газа при постоянном объёме;
- удельная теплоёмкость газа при постоянном объёме; - плотность газа.
- плотность газа. Па) и очень большие (
Па) и очень большие ( Па) давления.
Па) давления. ,
, - универсальная газовая постоянная, равная 8314,2 Дж/(кмоль·К);
- универсальная газовая постоянная, равная 8314,2 Дж/(кмоль·К); - молекулярная масса газа;
- молекулярная масса газа; .
. 0,6 Вт/(м·К).
0,6 Вт/(м·К). ,
, - удельная теплоёмкость жидкости при постоянном давлении;
- удельная теплоёмкость жидкости при постоянном давлении; - коэффициент, пропорциональный скорости распространения упругих волн в жидкости, не зависит от природы жидкости, но зависит от температуры, причём А С const.
- коэффициент, пропорциональный скорости распространения упругих волн в жидкости, не зависит от природы жидкости, но зависит от температуры, причём А С const. 0,7 Вт/(м·К).
0,7 Вт/(м·К). , на поверхности которой поддерживается температура
, на поверхности которой поддерживается температура  и
и  . Температура изменяется только по толщине пластика - по координате x. Такие процессы называют одномерными. Для них
. Температура изменяется только по толщине пластика - по координате x. Такие процессы называют одномерными. Для них  . Учитывая основной закон теплопроводности (
. Учитывая основной закон теплопроводности (
 .
. неизменна по толщине стенки. В большинстве практических задач приближенно предполагается, что и коэффициент теплопроводности
неизменна по толщине стенки. В большинстве практических задач приближенно предполагается, что и коэффициент теплопроводности 
 .
. Разделив переменные в этом уравнении и проинтегрировав левую часть и правую часть по
Разделив переменные в этом уравнении и проинтегрировав левую часть и правую часть по 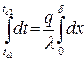 .
.
 .
. (К/Вт) - тепловым (термическим) сопротивлением стенки и обозначается
(К/Вт) - тепловым (термическим) сопротивлением стенки и обозначается  .
. .
. .
. :
:
 .
. .
. Если рассмотреть рис. 54, то– наименьшей теплопроводностью обладает материал второго слоя, а наибольшей – третьего.
Если рассмотреть рис. 54, то– наименьшей теплопроводностью обладает материал второго слоя, а наибольшей – третьего. .
. и закон Фурье имеет вид
и закон Фурье имеет вид
 .
. , поскольку площадь
, поскольку площадь  , через которую проходит тепловой поток, зависит от радиуса.
, через которую проходит тепловой поток, зависит от радиуса.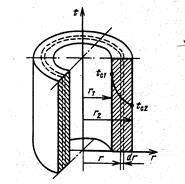
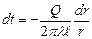 .Интеграл этого уравнения будет
.Интеграл этого уравнения будет
 от
от  до
до  ) даёт зависимость для расчёта теплового по
) даёт зависимость для расчёта теплового по  .
. .
.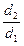 , близких к единице, расчёты должны проводиться с высокой точностью, так как может произойти большая ошибка при вычислении логарифма.
, близких к единице, расчёты должны проводиться с высокой точностью, так как может произойти большая ошибка при вычислении логарифма. .
. .
. ,
, .
. , наложенная на шар, не исключает теплопотери от него даже в стационарном режиме
, наложенная на шар, не исключает теплопотери от него даже в стационарном режиме  .
. и жидкости
и жидкости  :
: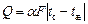 .
. называется коэффициентом теплоотдачи(Вт/(м2·/К)). Он характеризует интенсивность процесса теплоотдачи. Численное значение его равно тепловому потоку от единичной поверхности теплообмена при разности температур поверхности и жидкости в один Кельвин:
называется коэффициентом теплоотдачи(Вт/(м2·/К)). Он характеризует интенсивность процесса теплоотдачи. Численное значение его равно тепловому потоку от единичной поверхности теплообмена при разности температур поверхности и жидкости в один Кельвин: .
. .
.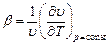 ,
, - удельный объём жидкости.
- удельный объём жидкости. (из уравнения Клайперона), этот коэффициент
(из уравнения Клайперона), этот коэффициент  .
. .
. ,
,

 …=
…=  ,
,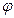 - значение любой физической величины.
- значение любой физической величины. (скорость, длина, вязкость, плотность, коэффициент теплоотдачи, температура) и так далее. Изучив одно явление на модели и зная постоянные подобия, может найти любые интересующие нас параметры во всех явлениях, подобных изученному поскольку согласно
(скорость, длина, вязкость, плотность, коэффициент теплоотдачи, температура) и так далее. Изучив одно явление на модели и зная постоянные подобия, может найти любые интересующие нас параметры во всех явлениях, подобных изученному поскольку согласно  .
.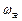 и теплофизических параметров жидкости:
и теплофизических параметров жидкости:



