Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энтальпия. Физические свойстваСодержание книги
Поиск на нашем сайте
Энтальпия Энтальпией термодинамического тела называют сумму внутренней энергии u и произведения pv. i = и + pv. Дифференцируя данное соотношение получим: di = du + pdv + vdp, или du + pdv = di - vdp. На основе первого закона термодинамикиdq = du + pdvпоследнее соотношение перепишется в виде: dq = di - vdp,илиdq = dh + dlt, где dlt - есть дифференциал технической работы (dlt = - vdp). Полученное уравнение является также второй формулировкой первого закона термодинамики, используя понятия энтальпии и технической работы. Величина i может также рассматриваться как параметр состояния термодинамического тела наряду с ранее введенными p, v, T, и. Физический смысл величины iможет пояснен на основе уравнения dq = di - vdp, которое для процесса p =const запишется как: dqp = di. (86) Откуда следует, что di есть элементарное количество теплоты, подведенное к термодинамическому телу в процессе постоянного давления.
Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями тела и не зависит от характера процесса. Энтропия является функцией состояния, поэтому её изменение в термодинамическом процессе определяется только начальными и конечными значениями параметров состояния. Изменение энтропии в основных термодинамических процессах: в изохорном в изобарном визотермическом в адиабатном
в политропном
ВНУТРЕННЯЯ ЭНЕРГИЯ РАБОЧЕГО ТЕЛА, ФИЗИЧЕСКИЙ СМЫСЛ И РАЗМЕРНОСТЬ. Внутренняя энергия – это вся энергия заключенная в теле или системе тел.Эту энергию можно представить в виде суммы отдельных видов энергий: кинетической энергии молекул, включающей энергию поступательного и вращательного движения молекул, а также колебательного движения атомов в самой молекуле; энергии электронов; внутриядерной энергии; энергии взаимодействия между ядром молекулы и электронами; потенциальной энергии или энергии положения молекул в каком либо внешнем поле сил; энергии электромагнитного излучения. Полную внутреннюю энергию тела принято обозначать U (Дж), а удельную внутреннюю энергию u (Дж/кг). Внутренняя энергия равна: Где – внутренняя кинетическая энергия молекул, внутренняя потенциальная энергия молекул, В технической термодинамике рассматриваются только такие процессы, в которых изменяются кинетическая и потенциальная составляющие внутренней энергии.
Изменение внутренней энергии идеального газа для любого процесса при бесконечно малом изменении состояния (для 1 кг) В теплотехнических расчётах обычно требуется знать изменение внутренней энергии
где Таким образом, изменение внутренней энергии идеального газа для любого процесса равно произведению средней теплоёмкости при постоянном объёме на разность температур газа.
ПРОЦЕССЫ ОБРАТИМЫЕ И НЕОБРАТИМЫЕ. РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ Термодинамический процесс – это последовательное изменение состояния тела, происходящее в результате энергетического взаимодействия рабочего тела с окружающей средой. Понятия обратимый и необратимый термодинамический процесс тесно связаны с равновесием системы. Рассмотрим такую термодинамическую систему у которой отсутствует теплообмен с окружающей средой (адиабатная термодинамическая система). Происходящие в такой системе термодинамические процессы называют обратимыми, если система в ходе прямого и обратного процесса вернется в исходное состояние без какого-либо дополнительного теплового воздействия окружающей среды на систему. В случае если система в ходе обратного процесса не может возвратиться в исходное состояние или для этого требуется подвод тепла, то такой процесс называется необратимым. Процесс при каждом изменении давления и температуры может быть обратимым только в том случае, когда на протяжении всего процесса от точки к точке термодинамической системы давление постоянно и температура в каждой точке равна температуре окружающей среды или их разность бесконечно мала. обратимые термодинамические процессы являются идеальным или теоретическим случаем. Все реальные процессы являются необратимыми, так как на практике выполнение условия квазистатичноститрудно выполнимо. Кроме того, необратимость процессов вызывается наличием внутреннего трения в рабочем теле и поверхностного трения в техническом оборудовании (течение в сопле, трение поверхности поршня о стенку цилиндра и т.д.). Для преодоления трения всегда необходимо затратить некоторое количество механической работы, которая в ходе процесса превращается в тепло.
ТЕПЛОЁМКОСТЬ РАБОЧЕГО ТЕЛА
Теплоемкостью называют количество теплоты, которое необходимо сообщить телу (газу), чтобы повысить температуру какой-либо количественной единицы на 1° С. Для определения значений перечисленных выше теплоемкостей достаточно знать величину одной какой-либо - из них. Удобнее, всего иметь величину мольной теплоемкости, тогда массовая теплоемкость:
а объемная теплоемкость: Объемная и массовая теплоемкости связаны между собой зависимостью: где Теплоемкость газа зависит от его температуры. По этому признаку различают среднюю и истинную теплоёмкость. Если q- количествотеплоты, сообщаемой единице количества газа (или отнимаемого от него) при изменении температуры газа от t1 до t2 то
Представляет собой среднюю теплоёмкость в пределах
ИЗОХОРНЫЙ ПРОЦЕСС ГАЗА
Изохорный процесс – процесс сообщения или отнятия теплоты при постоянном объеме газа (v = const). При постоянном объёме давление газа изменяется прямо пропорционально абсолютным температурам:
Внешняя работа газа при v = const равна нулю l=0. количество теплоты или изменение внутренней энергии газа:
Изохорный процесс на pv – диаграмме отображается прямой вертикальной линией - изохора. При положительном количестве тепла линия идёт снизу вверх.
Изменение энтропии находится:
ИЗОБАРНЫЙ ПРОЦЕСС ГАЗА.
Изобарный процесс – процесс сообщения или отнятия теплоты при постоянном давлении (р = const) Кривая процесса называется изобарой. Поскольку в изобарном процессе dp=0 то в системе не совершается техническая работа, а количество тепла необходимое для перехода тела из состояния 1 в состояние 2 определяется как:
Таким образом в изобарном термодинамическом процессе подводимое (отводимое) к телу количество тепла пропорционально изменению энтальпии в данном процессе.Данный вывод справедлив как для обратимого так и для необратимого процессов, при условии, что система находится в термодинамическом равновесии в начале и конце процесса. В случае обратимого процесса:
Изобарный процесс на pv – диаграмме отображается прямойгоризонтальной линией. При подводетепла в процесс линия простираетсяслева направо.
Механическая работа в таком процессе:
Удельная располагаемая (полезная) внешняя работа: Изменение удельной внутренней энергии: Из уравнения состояния идеального газа можно получить следующее соотношение для изобарного процесса:
Таким образом, при изобарном процессе объём идеальногогаза пропорционален абсолютной температуре. При расширении газа температура повышается, при сжатии уменьшается. Изменение энтропии в изобарном процессе может быть расчитано следующим образом:
АДИАБАТНЫЙ ПРОЦЕСС ГАЗА. Процесс протекающий без подвода и отвода теплоты, т.е. при отсутствии теплообмена с окружающей средой, называют адиабатным, а кривая этого процесса–адиабатой. Условия процесса: dq=0, q=0.
Т.к. dq=0, то согласно первому закону термодинамики: и Таким образом совершаемая рабочим телом механическая работа в адиабатном термодинамическом процессе равна уменьшению внутренней энергии тела, техническая работа при этом пропорциональна изменению (уменьшению) энтальпии. В обратимом диабатном процессе энтропия термодинамического тела не меняется: S=Const. Уравнение адиабаты в системе координат pv– диаграммы при постоянной теплоёмкости (
Зависимости между начальными и конечными параметрами процесса: между р и v между T и v между р и T Работу 1 кг газа находят по следующим формулам
Изменение внутренней энергии газа и работа адиабатного процесса равны по величине и противоположны по знаку.. Изменение внутренней энергии идеального газа в адиабатном процессе может быть также выражено уравнением
Второй закон термодинамики Второй закон термодинамики устанавливает направление протекания самопроизвольных тепловых процессов в природе и определяет условия превращения теплоты в работу. Закон утверждает, что теплота в природе самопроизвольно переходит только от тел более нагретых к менее нагретым. В соответствии со вторым законом термодинамики для превращения теплоты в работу в любом тепловом двигателе необходимо иметь два тела с различными температурами. Более нагретое тело будет источником теплоты для получения работы, менее нагретое – теплоприемником. При этом к. п. д. теплового двигателя всегда будет меньше единицы. Второй закон динамики математически может быть выражен:
Где dS – бесконечно малое приращении энтропии системы; dQ – бесконечно малое количество теплоты, полученной системой от источника теплоты; T- абсолютная температура источника теплоты. Знак неравенства соответствует необратимым процессам, а равенства - обратимым. Следовательно, аналитическое выражение второго закона термодинамики для бесконечно малого обратимого процесса примет вид dQ=TdS а т.к. согласно первому закону термодинамики dQ=dU+pdV то TdS=dU+pdV. Цикл Карно и его свойства. Цикл Карно. Состоит из двух изотерм и двух адиабат. Этот цикл представляет собой замкнутый процесс, совершаемый рабочим телом в идеальной тепловой машине при наличии двух источников теплоты: нагревателя и холодильника.
Цикл Карно в pv -диаграмме Процессы 1—2 и 3—4 являются изотермическими, а 2—3 и 4—1 — адиабатными. Начальная температура рабочего тела в цикле принимается равной температуре нагревателя T1. При изотермическом расширении от состояния 1 до состояния 2 рабочее тело получает от нагревателя количество теплоты q1 при температуре T1. На участке 2—3 рабочее тело адиабатно расширяется. При этом температура рабочего тела понижается от T1 до T2, а давление падаетот p2 до p3. При сжатии по изотерме 3—4 от рабочего тела отводится к холодильнику количество теплоты q2 при температуре T2. Дальнейшее сжатие по адиабате4—1 приводит к повышению температуры рабочего тела от T2 до T1, а рабочее тело возвращается в первоначальное состояние. Суммарная работа цикла lц графически изображается площадью 12341. Термический к. п. д. цикла: Количество подведённой теплоты:
Количество отведённой теплоты:
Работа цикла Карно
Термическийк.п.д. цикла:
Цикл с подводом теплоты при постоянном объёме состоит из двух адиабат и двух изохор
Характеристики цикла:
Количество подведённой теплоты:
Количество отведённой теплоты:
Работа цикла Термическийк.п.д. цикла:
Цикл с подводом теплоты при постоянном давлении состоит из двух адиабат, одной изобары и одной изохоры.
Характеристики цикла:
Количество подведённой теплоты:
Количество отведённой теплоты:
Работа цикла Термическийк.п.д. цикла:
Цикл с комбинированным подводом теплоты состоит из двух адиабат, двух изохор и одной изобары
Характеристики цикла
Количество подведённой теплоты
Количество отведённой теплоты
Термическийк.п.д. цикла
Таблицы водяного пара. Перегретый пар или насыщенный пар по своим свойствам значительно отличаются от идеальных газов. Уравнения для состояния паров весьма сложны и в расчётной практике не применяются. Для практических целей используют таблицы и диаграммы, составленные на основании опытных и теоретических данных. Таблицы составлены с высокой степенью точности для перегретых и насыщенных паров до температуры 10000С и давления 98,0 Мпа. В таблицах для насыщенного пара приведены температуры насыщения, давления, значения удельных объёмов, энтальпия и энтропия жидкости и сухого пара, теплота парообразования. В таблицах перегретого пара приведены для различных давлений и температур величины основных параметров: удельный объём, энтальпия и энтропия. i – S диаграмма водяного пара. Большим достоинством is диаграммы является то, что техническая работа и количество теплоты, участвующие в процессах, изображаются отрезками линий, а не площадями. При построении is- диаграммы по оси ординат откладывается удельная энтальпия пара, а по оси абсцисс – удельная энтропия. За начало координат принято состояние воды в тройной точке, где
Пользуясь данными таблиц водяного пара, на диаграмму наносят пограничные кривые жидкости и пара, сходящиеся в критической точке К. Пограничная кривая жидкости выходит из начала координат, т.к. в этой точке энтропию и энтальпию принимают равной нулю. Состояние воды отмечают точками на соответствующих изобарах. Линии изобар в области влажного пара являются прямыми наклонными линиями расходящимися веером от пограничной кривой жидкости. В изобарном процессе:
Угловой коэффициент наклона изобары к оси абсцисс в каждой точке диаграммы числено равен абсолютной температуре данного состояния. Т.к. в области влажного пара изобара совпадает с изотермой, то согласно последнему уравнению изобары влажного пара являются прямыми линиями:
Изотермы в области влажного пара совпадают с изобарами. В области перегретого пара они расходятся: изобары поднимаются вверх, а изотермы представляют собой кривые линии, обращённые выпуклостью вверх. На диаграмму наносят сетку изохор, которые имеют вид кривых, поднимающихся более круто вверх по сравнению с изобарами. Обратимый адиабатный процесс изображается вертикальной прямой. Область лежащая ниже изобары тройной точки изображает состояния смеси пар + лёд.
Адиабатический процесс водяного пара. Изображение процесса в p – V, i – S и T –S диаграммах. Адиабатный процесс совершается без подвода и отвода теплоты, и энтропия рабочего тела при обратимом процессе остаётся постоянной величиной: s=const. Поэтому на is и Ts- диаграммах адиабаты изображаются вертикальными прямыми: рис. а и б
При адиабатном расширении давление и температура пара уменьшаются; перегретый пар переходит в сухой, а затем во влажный пар. Из условий постоянства энтропии возможны определение конечных параметров пара, если известны параметры начального и один параметр конечного состояний. На pv - диаграмме обратимый адиабатный процесс изображается некоторой кривой (рис. в)
Удельная работа в адиабатном процессе определяется из уравнения: . Изменение удельной внутренней энергии:
Многоступенчатое сжатие в компрессоре. Для получения газа высокого давления применяют многоступенчатые компрессоры
в которых сжатие газа осуществляется политропно в нескольких последовательно соединённых цилиндрах с промежуточным его охлаждением после каждого сжатия. Применение сжатия газа в нескольких цилиндрах понижает отношение давлений в каждом из них и повышает объёмныйк.п.д. компрессора. Кроме того, промежуточное охлаждение газа после каждой ступени улучшает условия смазки поршня в цилиндре и уменьшает расход энергии на привод компрессора.
идеальная индикаторная диаграмма трёхступенчатого компрессора, где 0-1 – линия всасывания в первую ступень; 1-2 – политропный процесс сжатия в первой ступени; 2-а – линия нагнетания из первой ступени в первый охладитель; а-3 – линия всасывания во вторую ступень; 3-4 – политропный процесс сжатия во второй ступени; 4-в – линия нагнетания из второй ступени во второй охладитель; в-5 – линия всасывания в третью ступень; 5-6 - политропный процесс сжатия в третьей ступени; 6-с – линия нагнетания из третьей ступени в резервуар или на производство. Отрезки 2-3, 4-5 изображают уменьшение объёма газа в процессе при постоянном давлении от охлаждения в первом и втором охладителях. Охлаждение рабочего тела во всех охладителях производится до одной и той же температуры, равной начальной Т1, поэтому температуры газа в точках 1, 3 и 5 одинаковые и лежат на изотерме 1 – 7. Отношение давлений во всех ступенях обычно берётся одинаковым:
При одинаковых отношениях давлений во всех ступенях, равенстве начальных температур и равенстве показателей политропы равны между собой и конечные температуры газа в отдельных ступенях компрессора:
Степень увеличения давления в каждой ступени Степень увеличения давления в каждой ступени равна корню z-й степени из отношений конечного давления к начальному При равенстве температур газа у входа в каждую ступень и равенстве отношений давлений во всех цилиндрах получаем равенство затраченных работ во всех ступенях компрессора:
Во второй ступени
Работа в третьей ступени
Откуда l1=l2=l3 Полная удельная работа в джоулях, расходуемая на сжатие газа в трёх ступенях компрессора: lк=3l1 При одинаковых условиях сжатия газа количества теплоты, отводимые от газа в отдельных ступенях, равны между собой:
Теплоту отводимую от газа в любом охладителе при изобарном процессе охлаждения, находим по формуле:
В Ts- диаграммах процессы адиабатного сжатия изображены прямыми 1-2, 3-4, 5-6, а процессы охлаждения кривыми 2-3, 4-5, 6-7.
Процессы политропного сжатия изображены кривыми 1-2, 3-4, 5-6, а процессы охлаждения в охладителях - линиями 2-3, 4-5, 6-7.
Цикл ДВС со сгоранием при V=const
На рисунке изображена индикаторная диаграмма двигателя, работающего с быстрым сгоранием топлива при постоянном объёме. В качестве горючего используется бензин, светильный или генераторный газ, спирты и др. При ходе поршня из левого мёртвого положения в крайнее правое через всасывающий клапан засасывается горючая смесь. Этот процесс изображён кривой 0-1, называется линией всасывания, она не является термодинамическим процессом, т.к. в нём основные параметры не изменяются, а изменяются только масса и объём смеси в цилиндре. При обратном движении поршня всасывающий клапан закрывается, происходит сжатие горючей смеси. Изображается кривой 1-2, называется линией сжатия. В точке 2 происходит воспламенение горючей смеси от электрической искры. Сгорание горючей смеси происходит почти мгновенно, т.е. практически при постоянном объёме. Этот процесс изображён кривой 2-3. В результате сгорания топлива температура газа резко возрастает и давление увеличивается (точка 3). Затем продукты горения расширяются. Поршень перемещается в правое мёртвое положение, и газы совершают полезную работу. На индикаторной диаграмме процесс расширения изображается кривой 3-4, называемой линией расширения. В точке 4 открывается выхлопной клапан, и давление в цилиндре падает почти до наружного давления. При дальнейшем движении поршня справа на лево из цилиндра удаляются продукты сгорания через выхлопной клапан при давлении, несколько превышающим атмосферное давление. Изображается кривой 4-0 и называется линией выхлопа. Такой рабочий процесс совершается за четыре хода поршня или за два оборота вала. Такие двигатели называются четырёхтактными. Цикл с подводом теплоты при постоянном объёме состоит из двух адиабат и двух изохор
Характеристиками цикла являются:
Количество подведённой теплоты:
Количество отведённой теплоты:
Работа цикла Термическийк.п.д. цикла:
Цикл ДВС со сгоранием при p=const Изучение циклов с подводом количества теплоты при постоянном объёме показало, что для повышения экономичности двигателя, работающего по этому циклу, необходимо применять высокие степени сжатия. Воздух при большом сжатии имеет настолько высокую температуру что подаваемое в цилиндр топливо самовоспламеняется без запальных приспособлений. Раздельное сжатие воздуха и топлива позволяет использовать любое жидкое тяжёлое и дешёвое топливо – нефть, мазут, смолы, каменноугольные масла. Таким достоинством обладают двигатели, работающие с постепенным сгоранием топлива при постоянном давлении. В них воздух сжимается в цилиндре двигателя, а жидкое топливо распыляется сжатым воздухом от компрессора. Идеальный цикл двигателя с постепенным сгоранием топлива при постоянном давлении, т.е. цикл с подводом количества теплоты при постоянном давлении осуществляется следующим образом.
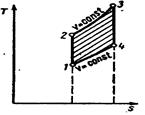
Газообразное рабочее тело с начальными параметрами p1, v1, T1 сжимается по адиабате 1-2; затем телу по изобаре 2-3 сообщается некоторое количество теплоты q1. От точки 3 рабочее тело расширяется по адиабате 3-4. По изохоре 4-1 рабочее тело возвращается в первоначальное состояние, при этом в теплоприёмник отводится теплота q2. Характеристики цикла:
Количество подведённой теплоты:
Количество отведённой теплоты:
Работа цикла Термическийк.п.д. цикла:
Цикл ДВС с подводом тепла при V и p =const В бескомпрессорном двигателе высокого сжатия со смешанным подводом количества теплоты жидкое топливо топливным насосом подаётся через топливную форсунку в головку цилиндра в виде мельчайших капелек. Попадая в нагретый воздух, топливо самовоспламеняется и горит в течении всего периода, пока открыта форсунка: вначале при постоянном объёме, а затем при постоянном давлении.
Идеальный цикл двигателя со смешанным подводом количества теплоты изображён в pv–и Ts–диаграммах. рабочее тело с начальными параметрами p1, v1, T1 сжимается по адиабате 1-2 до точки 2. По изохоре 2-3 к рабочему телу подводится первая доля теплоты Характеристики цикла являются:
Определим термический КПД цикла при условии что теплоёмкости cp, cv и показатель адиабаты k=cp / cv постоянны:
Первая доля подведённой теплоты:
Вторая доля подведённого количества теплоты:
Количество отведённой теплоты:
Термический КПД цикла
Формула Майера. Особое значение в термодинамике имеют теплоемкости газа при постоянном давлении, т.е. в изобарном процессе –
Отношение теплоемкостей
где k – показатель адиабаты. Понятие «Холодильный коэффициент» Холодильный коэффициент безразмерная величина (обычно больше единицы), характеризующая энергетическую эффективность работы холодильной машины; равна отношению холодопроизводительности к количеству энергии (работе), затраченной в единицу времени на осуществление холодильного цикла. Определяется типом холодильного цикла, по котором у работает машина, совершенством её основных элементов и для одной и той же машины зависит от температурных условий её работы. Холодильный коэффициент идеальной холодильной машины, работающей по обратному циклу Карно:
где Tмин и Tмакс – соответственно низшая и высшая температуры в цикле.
Холодильный коэффициент воздушной холодильной машины (рисунок) где T1 и T2 – соответственно температуры начала и конца адиабатного сжатия; T3 и T4 – температуры начала и конца адиабатного расширения в детандере.
Повторный перегрев пара Исследование работы паротурбинной установки показывает, что повышение начального давления и уменьшение конечного давления ведёт к увеличению КПД цикла. Однако одно повышение начального давления увеличивает конечную влажность пара. Для уменьшения влажности пара в конце расширения повышают начальную температуру его. Одним из способов повышения степени сухости пара на выходе из турбины является вторичный его перегрев. Перегретый пар из котла с начальным давлением и температурой поступает в первый цилиндр турбины, состоящий из нескольких ступеней, где расширяется по адиабате до некоторого давления p1. Образовавшийся пар отводят в специальный перегреватель, где он подвергается вторичному перегреву при постоянном давлении. Затем его снова возвращают в турбину, где пар продолжает расширяться до давления в конденсаторе.
Точка 1 соответствует начальному состоянию пара; точка 2 – конечному состоянию пара за турбиной после вторичного перегрева. Конечная степень сухости в результате введения промежуточного перегрева повышается от x2 до x1. Кроме того вторичный перегрев пара даёт некоторый экономический эффект (2-3%), если средняя температура подвода теплоты в дополнительном цикле 7-2-2’-6-7 будет выше средней температуры подвода теплоты в цикле с однократным перегревом, и эффект будет тем больше, чем выше температура в начальной и конечной точках промежуточного перегрева. При давлениях близких к критическому и сверхкритическому, иногда применяют два промежуточных перегрева и более. Тогда термический КПД цикла Где
Удельный расход пара
Энтальпия Энтальпией термодинамического тела называют сумму внутренней энергии u и произведения pv. i = и + pv. Дифференцируя данное соотношение получим: di = du + pdv + vdp, или du + pdv = di - vdp. На основе первого закона термодинамикиdq = du + pdvпоследнее соотношение перепишется в виде: dq = di - vdp,илиdq = dh + dlt, где dlt - есть дифференциал технической работы (dlt = - vdp). Полученное уравнение является также второй формулировкой первого закона термодинамики, используя понятия энтальпии и технической работы. Величина i может также рассматриваться как параметр состояния термодинамического тела наряду с ранее введенными p, v, T, и. Физический смысл величины iможет пояснен на основе уравнения dq = di - vdp, которое для процесса p =const запишется как: dqp = di. (86) Откуда следует, что di есть элементарное количество теплоты, подведенное к термодинамическому телу в процессе постоянного давления.
Изменение энтальпии в любом процессе определяется только начальным и конечны
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.130 (0.019 с.) |


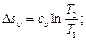

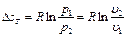


 – постоянная интегрирования.
– постоянная интегрирования.
 , а не её абсолютное значение; поэтому начало отсчёта (0 К или 00 С) для конечного результата (
, а не её абсолютное значение; поэтому начало отсчёта (0 К или 00 С) для конечного результата (
 - средняя массовая теплоёмкость при постоянном объёме в пределах
- средняя массовая теплоёмкость при постоянном объёме в пределах 


 - плотность газа при нормальных условиях.
- плотность газа при нормальных условиях.
 . Предел этого отношения, когда разность температур стремиться к нулю, называют истинной теплоёмкостью.
. Предел этого отношения, когда разность температур стремиться к нулю, называют истинной теплоёмкостью.












 )для идеального газа:
)для идеального газа:  где
где  - показатель адиабаты
- показатель адиабаты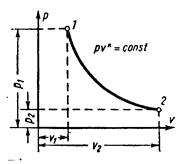
 ,
,











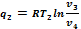



 -степень сжатия
-степень сжатия степень повышения давления
степень повышения давления



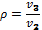 степень предварительного расширения.
степень предварительного расширения.


 ;
; 



 ,
,  .
.
 или
или 
 , а это и есть уравнение прямой линии. В области перегретого пара изобары имеют кривизну с выпуклостью, обращённой вниз. В области влажного пара наносится сетка линий постоянной сухости пара (x=const) которые сходятся в критической точке К.
, а это и есть уравнение прямой линии. В области перегретого пара изобары имеют кривизну с выпуклостью, обращённой вниз. В области влажного пара наносится сетка линий постоянной сухости пара (x=const) которые сходятся в критической точке К.





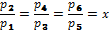

 или приzступеней
или приzступеней 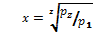




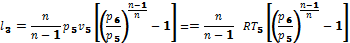

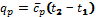



 – степень сжатия
– степень сжатия –степень повышения давления
–степень повышения давления



 . По изобаре 3-4 подводится вторая доля теплоты
. По изобаре 3-4 подводится вторая доля теплоты  . От точки 4 рабочее тело расширяется по адиабате 4-5. По изохоре 5-1 рабочее тело возвращается в первоначальное состояние – в точку 1, при этом отводится теплота
. От точки 4 рабочее тело расширяется по адиабате 4-5. По изохоре 5-1 рабочее тело возвращается в первоначальное состояние – в точку 1, при этом отводится теплота  в теплоприёмник.
в теплоприёмник.

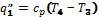


 и при постоянном объеме, т.е. в изохорном процессе –
и при постоянном объеме, т.е. в изохорном процессе –  . Эти теплоемкости связываются формулой Майера
. Эти теплоемкости связываются формулой Майера
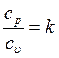

 ,
,


 –адиабатноетеплопадение в первом и втором цилиндрах турбины;
–адиабатноетеплопадение в первом и втором цилиндрах турбины; – количество теплоты, подведённое в котле и первом перегревателе;
– количество теплоты, подведённое в котле и первом перегревателе;