
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3.6 Важнейшие замкнутые классы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть M Í Р 2. Замыканием М называется множество всех функций из P 2, которые можно выразить формулами над М. Замыкание М обозначается [ M ]. Множество функций М называется замкнутым классом, если [ M ]= M. Пример: 1) P 2 – замкнутый класс. 2) Множество {1, x 1Å x 2} не является замкнутым классом. Его замыканием будет класс линейных функций: [{1, x 1 Å x 2}] = { f (x 1,..., xn) = c 0 Å c 1 x 1 Å... Å cnxn }. Действительно, по определению формулы над М, функция f (G 1, x 3), где f – есть сумма по модулю 2, G 1 – функция х 1 Å х 2, будет формулой над М: f (G 1, x 3) = (x 1 Å x 2) Å x 3. В терминах замыкания и замкнутого класса можно дать другое определение полноты, эквивалентное исходному: М – полная система, если [ M ] = P 2. 3) A = { f (x 1,..., xn)| f (1, 1,..., 1) = 0} – незамкнутый класс. Возьмем формулу над этим множеством. Пусть f, g 1,..., gn Î A, т.е. f (1, 1,..., 1) = 0, g 1(1, 1,..., 1) = 0, тогда f (g 1,..., gn) Î [ A ]. Посмотрим, принадлежит ли функция f (g 1,..., gn) множеству А. f (g 1(1,..., 1), g 2(1,..., 1),..., gn (1,..., 1) = f (0,..., 0)), но f (0,..., 0) не обязано быть равным 0. Действительно, пусть g 1(x 1, x 2) = x 1 Å x 2, g 2(x) = x Î A. Возьмем g 2(g 1(x 1, x 2)) = x 1 Å x 2 Î [ A ], g 2(g 1(1, 1)) = 1 Å 1 = 0, следовательно, g 2(g 1(x 1, x 2)) Ï A, отсюда [ A ] ¹ A и А – незамкнутый класс. Важнейшие замкнутые классы в Р2 1)Т0 - класс функций, сохраняющих константу 0. Т 0 = { f (x 1,..., xn | f (0,..., 0) = 0, n = 1, 2,...}. Покажем, что Т 0 является собственным подмножеством Р 2, т.е. Т 0 ¹ Æ и Т 0 Ì Р (не совпадает с Р 2). Для этого достаточно привести примеры функций, входящих в Т 0, и примеры функций из Р2, не входящих в Т 0: x 1& x 2, x 1Ú x 2, x Î Т 0 и x 1| x 2, x 1 Число функций, зависящих от n переменных и принадлежащих Т 0, будет равно 2)T 1 – класс функций, сохраняющих константу 1. T 1 = { f (x 1,...) | f (1, 1,...) = 1}; x 1& x 2, x 1Ú x 2, x Î T 1, х 1Å х 2, x 1 Покажем, что [ T 1] Í T 1, обратное включение следует из определения формулы и замыкания. Так как тождественная функция входит в Т 1, можно рассмотреть Ф = f (f 1,..., fn) Î [ T 1], где f, f 1,..., fn Î T 1. Найдем Ф (1,..., 1) = f (f 1(1,..., 1),..., fn (1,..., 1)) = f (1,..., 1) = 1, следовательно, Ф = f (f 1,..., fn) Î T 1, отсюда следует [ T 1] = T 1. 3)S – класс самодвойственных функций . S = { f (x 1,...)| f * = f }; x, 4)L – класс линейных функций . L = { f (x 1,...)| f = c 0Å c 1 x 1Å...Å cnxn }; очевидно, L ¹ Æ, с другой стороны L ¹ P 2, так как x 1& x 2 Ï L. Заметим, что тождественная функция принадлежит L и | L (n)| = 2 n +1. Покажем, что [ L ] Í L. Рассмотрим Ф = f (f 1,..., fm), где f, f 1,..., fn Î L. Тогда Ф = а 0 Å а 1(с 10 Å с 11 х 1 Å...Å c 1 nxn 1) Å a 2(c 20 Å c 21 x 1 Å c 22 x 2Å...Å c 2 nxn 2)Å...Å an (cm 0 Å cm 1x1 Å... Å cmnxnm) = в 0 Å в 1 х 1 Å...Å вnхn Þ Ф Î L. 5)М – класс монотонных функций. Набор Функция f (x 1,..., xn) называется монотонной, если для двух наборов Для числа монотонных функций, зависящих от n переменных, существуют оценки сверху и снизу, но точное число сосчитать не удается. Покажем, что М замкнутый класс. Рассмотрим функцию Ф Î[ M ], Ф = f (f 1,..., fm), где f, f 1,..., fm Î M, причем можем считать, что все они зависят от n переменных. Пусть набор Функция f есть суперпозиция над M, если f реализуется некоторой формулой над M. Лемма о немонотонной функции. Отрицание можно получить суперпозицией констант 0 и 1, тождественной функции и немонотонной функции. Доказательство. Пусть f (x 1,..., xn) – немонотонная функция. Тогда существуют наборы Классы T 0, T 1, L, S, M пересекаются, но не совпадают, что видно из следующей таблицы, где «+» означает, что функция принадлежит данному классу и «-» – не принадлежит.
A ={ x, Задачи 1. Доказать, что пересечение любых двух замкнутых классов замкнуто. 2. Доказать, что объединение двух замкнутых классов не всегда замкнуто Тема 3.7 Теорема Поста.
Для того чтобы система функций была полной, необходимо и достаточно, чтобы она не содержалась целиком ни в одном из классов T 0, T 1, L, S, M. Доказательство. Докажем необходимость этого условия. Пусть система N = { f 1, f 2,... fs,...} полна в Р 2, покажем, что тогда она не лежит целиком в Q, где через Q обозначим любой из классов T 0, T 1, L, S, M. Докажем от противного, пусть N Í Q, очевидно, [ N ] Í [ Q ] = Q, но [ N ] = P 2, т.к. N – полна в Р 2, отсюда Р 2= Q, но это не так. Необходимость доказана. Докажем достаточность. Пусть F = { f 0, f 1, fL, fm, fs }, где f 0Ï T 0, f 1Ï T 1, fL Ï L, fs Ï S и fm Ï M. Покажем, что суперпозицией функций системы F можно получить полную систему G = { x 1& x 2, 1. Пусть g (x) = f 0(x, …, x). Тогда g (0) = f (0, …, 0) = 1. Далее возможны два случая: g (1) = 1. Тогда g (x) º 1. Функция h (x) = f 1(g (x), …, g (x)) = f 1(1, …, 1) = 0, т.е. h (x) º 0. Получили константы 0 и 1; g(1) = 0. Тогда g (x) = В обоих случаях получили обе константы. 2. По лемме о немонотонной функции суперпозицией над { fm, 0, 1} можно получить отрицание. 3. По лемме о нелинейной функции суперпозицией над { fL, 1, Следствие. Всякий замкнутый класс функций из Р 2, не совпадающий с Р 2 содержится, по крайней мере, в одном из замкнутых классов T 0, T 1, L, S, M. Действительно, если N не является подмножеством Q, то [ N ] = P 2, что неверно. Примеры использования теоремы Поста. 1. Покажем, что система функций { f 1 = x 1 x 2, f 2 =0, f 3 =1, f 4 = x 1Å x 2Å x 3} полна в Р 2. Составим таблицу, которая называется критериальной:
Из таблицы видно, что какой бы класс мы ни взяли, всегда есть функция из данной системы, которая в этот класс не входит. Можно сформулировать следующее правило: для того чтобы система функций была полна, необходимо и достаточно, чтобы в каждом столбце критериальной таблицы был хотя бы один «минус». Отметим еще одно обстоятельство, касающееся приведенной системы. Какую бы функцию из этой системы мы ни удалили, система станет неполной, действительно, { f 2, f 3, f 4}Ì L, { f 1, f 3, f 4}Ì T 1, { f 1, f 2, f 4}Ì T 0, { f 1, f 2, f 3}Ì M. 2. Мы знаем, что система { x 1| x 2} – полна в Р 2. Какова для нее критериальная таблица? x 1| x 2=
3. Составим критериальную таблицу для другой полной системы функций из Р2: {0, 1, x 1 x 2, x 1Å x 2}.
Согласно критериальной таблице, полной является и система {1, x 1 x 2, x 1Å x 2}. Константа 0 введена в эту систему для удобства, тогда мы можем записать полином Жегалкина в виде, где а 4. Выясним, полна ли система
и А – полная система функций. Система функций { f 1,..., fs,...} называется базисом в Р 2,если она полна в Р 2, но любая ее подсистема не будет полной. Например, система функций { x 1& x 2, 0, 1, x 1
Контрольная работа Вариант I 1. Составить таблицу истинности для булевой функции:
2. Составить СДНФ и СКНФ для:
3. Найти минимальную (сокращённую) ДНФ для в.ф. ы
4. Определить является ли следующая система функций полной {0,1,x, 5. Дана формула
Вариант II 1. Составить таблицу истинности для булевой функции:
2. Составить СДНФ и СКНФ для:
3. Найти минимальную (сокращённую) ДНФ для в.ф. ы
4. Определить является ли следующая система функций полной
5. Дана формула
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 449; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.161.119 (0.008 с.) |

 x 2,
x 2,  Ï Т 0. Покажем далее, что [ Т 0] = Т 0. Вложение Т 0 Í [ Т 0] очевидно, так как по определению формулы любая функция из Т 0 является формулой над Т 0 и, следовательно, принадлежит [ Т 0]. Покажем, что [ Т 0]Í Т 0. Для этого надо показать, что Ф = f (f 1,..., fm) Î [ Т 0], если все функции f, f 1, f 2, f 3,..., f m Î Т 0. Надо заметить, что в формуле в качестве функции f 1 могут быть взяты переменные, которые мы договорились считать тождественными функциями. Тождественная функция принадлежит классу Т 0, поэтому достаточно показать, что Ф = f (f 1,..., fm) Î Т 0. Для этого рассмотрим следующую функцию: Ф (0,..., 0) = f (f 1(0,..., 0), f 2(0,..., 0),...) = f (0,..., 0) = 0.
Ï Т 0. Покажем далее, что [ Т 0] = Т 0. Вложение Т 0 Í [ Т 0] очевидно, так как по определению формулы любая функция из Т 0 является формулой над Т 0 и, следовательно, принадлежит [ Т 0]. Покажем, что [ Т 0]Í Т 0. Для этого надо показать, что Ф = f (f 1,..., fm) Î [ Т 0], если все функции f, f 1, f 2, f 3,..., f m Î Т 0. Надо заметить, что в формуле в качестве функции f 1 могут быть взяты переменные, которые мы договорились считать тождественными функциями. Тождественная функция принадлежит классу Т 0, поэтому достаточно показать, что Ф = f (f 1,..., fm) Î Т 0. Для этого рассмотрим следующую функцию: Ф (0,..., 0) = f (f 1(0,..., 0), f 2(0,..., 0),...) = f (0,..., 0) = 0.

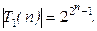
 , x 1Å x 2Å x 3Î S, x 1& x 2, x 1Ú x 2, x 1Å x 2Ï S, следовательно, S – собственное подмножество Р 2. | S (n)| =
, x 1Å x 2Å x 3Î S, x 1& x 2, x 1Ú x 2, x 1Å x 2Ï S, следовательно, S – собственное подмножество Р 2. | S (n)| = 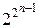 . Покажем, что [ S ]Í S. Ф = f (f 1,..., fn) Î [ S ], если f, f 1,..., fn Î S, а также, что Ф Î S. По принципу двойственности, Ф * = f *(f 1*,..., fn *) = f (f 1,..., fn) = Ф, отсюда S – замкнутый класс.
. Покажем, что [ S ]Í S. Ф = f (f 1,..., fn) Î [ S ], если f, f 1,..., fn Î S, а также, что Ф Î S. По принципу двойственности, Ф * = f *(f 1*,..., fn *) = f (f 1,..., fn) = Ф, отсюда S – замкнутый класс. = (a 1,..., an) предшествует набору
= (a 1,..., an) предшествует набору  = (b 1,..., bn) и обозначается
= (b 1,..., bn) и обозначается  , если для 1£ i £ n ai £ bi, например:
, если для 1£ i £ n ai £ bi, например: 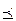
 = (a 1,..., an),
= (a 1,..., an),  и
и  , для которых
, для которых 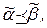 но
но  Пусть i 1, …, ik есть все те номера аргументов, для которых
Пусть i 1, …, ik есть все те номера аргументов, для которых  , p =1, …, k. На всех остальных аргументных местах j имеем aj = bj. В выражении
, p =1, …, k. На всех остальных аргументных местах j имеем aj = bj. В выражении  заменим нули на местах i 1, …, ik на x. В результате получим функцию g (x), для которой g (0) = f (
заменим нули на местах i 1, …, ik на x. В результате получим функцию g (x), для которой g (0) = f (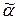 ) = 1 и g (1) = f (
) = 1 и g (1) = f (
 } можно получить конъюнкцию. Теорема доказана.
} можно получить конъюнкцию. Теорема доказана. = x 1 x 2Å1.
= x 1 x 2Å1. равны 0, если члены х
равны 0, если члены х  х
х  ... х
... х  , в полиноме отсутствуют.
, в полиноме отсутствуют. . Составим критериальную таблицу, очевидно
. Составим критериальную таблицу, очевидно  . Чтобы показать, что
. Чтобы показать, что 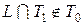 , достаточно найти одну функцию
, достаточно найти одну функцию 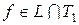 и
и  . Возьмем
. Возьмем  , удовлетворяющую требуемым условиям. Если f
, удовлетворяющую требуемым условиям. Если f  S \ T 0, то f (0,..., 0) = 1, f (1,..., 1)=0, следовательно, f
S \ T 0, то f (0,..., 0) = 1, f (1,..., 1)=0, следовательно, f 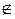 M, f
M, f  x 2 x 3
x 2 x 3  T 1
T 1


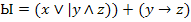
 }
}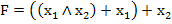 . Определите булевую функцию, которую реализует данная формула (составить таблицу истинности)
. Определите булевую функцию, которую реализует данная формула (составить таблицу истинности)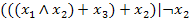

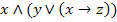

 . Определите булевую функцию, которую реализует данная формула (составить таблицу истинности)
. Определите булевую функцию, которую реализует данная формула (составить таблицу истинности)


