
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4.6 Бинарные отношения и их свойства.
Декартовым произведением двух множеств называется Бинарным отношением между множествами А и В называется всякое подмножество их декартового произведения.
Бинарное отношение – множество, состоящее из двоек чисел. Если Среди всех бинарных отношений выделяют две и дают им следующие названия: 1. универсальное бинарное отношение – состоит из всех элементов множества 2. нулевое бинарное отношение – не содержит ни одного элемента и совпадает с пустым множеством. Бинарным отношением на множестве А называется любое подмножество Обратным бинарным отношением к бинарному отношению Р называется множество Р-1: Свойства бинарных отношений: 1) Бинарное отношение Р на множестве А называется рефлексивным, если для любого элемента х множества А, двойка чисел 2) Бинарное отношение Р называется симметричным, если из того что двойка чисел Бинарное отношение Р называется антисимметричным если из того, что двойка чисел 3) Бинарное отношение называется транзитивным, если из того, что 4) Бинарное отношение Р называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно. Самостоятельная работа №10. Контрольная работа
Вариант 1
Первый уровень сложности – задачи №№ 1,2,3 – оценка “удовлетворительно” Второй уровень сложности – любые четыре задачи – оценка “хорошо” Третий уровень сложности – все задачи – оценка “отлично”
1. Найти области истинности следующих предикатов: а). « б). « в). « 2. Дана формула 3. Высказывательная форма x+y=z, с переменными, упорядоченными по алфавиту и принимающими значения из множества однозначных натуральных чисел, задаёт предикат F(x,y,z). Выпишите тройки чисел, компоненты которых находятся в отношении F. 4. Задано бинарное отношение 5. Пусть бинарные отношения P и S определены на М, где М-множество всех людей следующим образом:
P= {(x,y) | x,y M,x является отцом y} S= {(x,y) | x,y M,x - дочь y} Описать явно следующие отношения: а). PS b)
Вариант 2
Первый уровень сложности – задачи №№ 1,2,3 – оценка “удовлетворительно” Второй уровень сложности – любые четыре задачи – оценка “хорошо” Третий уровень сложности – все задачи – оценка “отлично”
1. Найти области истинности следующих предикатов: а). « б). « в). « 2. Дана формула 3. Высказывательная форма «x – среднее арифметическое y и z», с переменными, упорядоченными по алфавиту и принимающими значения из множества однозначных натуральных чисел, задаёт предикат F(x,y,z). Выпишите тройки чисел, компоненты которых находятся в отношении F. 4. Задано бинарное отношение 5. Пусть бинарные отношения P и S определены на М, где М-множество всех людей следующим образом: P= {(x,y) | x,y S= {(x,y) | x,y Описать явно следующие отношения: а).
Вариант 3
Первый уровень сложности – задачи №№ 1,2,3 – оценка “удовлетворительно” Второй уровень сложности – любые четыре задачи – оценка “хорошо” Третий уровень сложности – все задачи – оценка “отлично”
1. Найти области истинности следующих предикатов: а). « б). « в). « 2. Дана формула 3. Высказывательная форма «y равен квадратному корню из произведения чисел x и z», с переменными, упорядоченными по алфавиту и принимающими значения из множества однозначных натуральных чисел, задаёт предикат F(x,y,z). Выпишите тройки чисел, компоненты которых находятся в отношении F. 4. Задано бинарное отношение 5. Пусть бинарные отношения P и S определены на М, где М-множество всех людей следующим образом:
P= {(x,y) | x,y S= {(x,y) | x,y Описать явно следующие отношения: а). PS b)
Вариант 4
Первый уровень сложности – задачи №№ 1,2,3 – оценка “удовлетворительно” Второй уровень сложности – любые четыре задачи – оценка “хорошо” Третий уровень сложности – все задачи – оценка “отлично”
1. Найти области истинности следующих предикатов: а). « б). « в). « 2. Дана формула 3. Высказывательная форма «x+y делится нацело на z», с переменными, упорядоченными по алфавиту и принимающими значения из множества однозначных натуральных чисел, задаёт предикат F(x,y,z). Выпишите тройки чисел, компоненты которых находятся в отношении F. 4. Задано бинарное отношение 5. Пусть бинарные отношения P и S определены на М, где М-множество всех людей следующим образом: P= {(x,y) | x,y S= {(x,y) | x,y Описать явно следующие отношения: а).
|
||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 565; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.125.171 (0.017 с.) |
 .
.
 тогда бинарным отношением между А и В будет 2mn.
тогда бинарным отношением между А и В будет 2mn.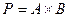 .
.
 .
.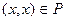 .
. следует, что
следует, что  .
. .
. следует, что
следует, что  .
. на множестве действительных чисел R»
на множестве действительных чисел R» на множестве действительных чисел R»
на множестве действительных чисел R»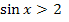 на множестве действительных чисел»
на множестве действительных чисел» . Являются ли вхождения переменной x свободными?
. Являются ли вхождения переменной x свободными? . Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность).
. Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность). c).
c).  d)
d) 
 x,y
x,y 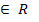 - множество действительных чисел»
- множество действительных чисел» на множестве действительных чисел R»
на множестве действительных чисел R» если
если  и
и  »
» . Являются ли вхождения переменной x связанными?
. Являются ли вхождения переменной x связанными? . Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность).
. Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность). M, x является отцом y}
M, x является отцом y} M, x - дочь y}
M, x - дочь y} b)
b)  d)
d) 
 x
x  на множестве натуральных чисел N»
на множестве натуральных чисел N» на множестве натуральных чисел N»
на множестве натуральных чисел N» . Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность).
. Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность).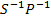
 x,y
x,y  на множестве действительных чисел R»
на множестве действительных чисел R» на множестве действительных чисел»
на множестве действительных чисел»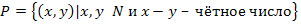 . Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность).
. Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность). b)
b)  c).PS d)
c).PS d) 



