Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2.4 Конъюнктивная нормальная форма.Содержание книги
Поиск на нашем сайте
Высказывательная форма, состоящая из переменных или отрицательных переменных, применением только одной операции конъюнкции, называется элементарной конъюнкцией. Высказывательная форма, состоящая из элементарных дизъюнкций, применением только одной операции конъюнкции называется конъюнктивной нормальной формой (КНФ). Теорема: Для любой высказывательной формы существуют равносильные ДНФ и КНФ. Доказательство: 1) по теореме 1 существует Ы* - приведенная равносильная высказывательная форма, т.е. 2) Для того чтобы получить КНФ необходимо к высказывательной форме применить второй дистрибутивный закон, также нужное число раз. Способы построения ДНФ и КНФ для любой высказывательной формы: 1) составляется Ы* - приведенная высказывательная форма, являющаяся равносильной (т.е. применяется необходимое число раз законы Моргана, импликации) 2) для получения ДНФ к Ы* применяется первый дистрибутивный закон: для получения КНФ к Ы* применяется второй дистрибутивный закон: Совершенной конъюнктивной формулой формулы алгебры высказываний (СКНФ) называется КНФ, в которой: 1. различны все члены конъюнкции; 2. различны все члены каждой дизъюнкции; 3. ни одна дизъюнкция не содержит переменную вместе с отрицанием этой переменной; 4. каждая дизъюнкция содержит все переменные, входящие в исходную формулу, т. е. имеет вид
где конъюнкция берется по всем наборам с=(с1, с2, …, сn) из 0 и 1, для которых F(c)=0. Теорема (о СКНФ). Для всякой не равной тождественной единице формулы логики высказываний F(x1, x2, …, xn) существует такая формула F1, зависящая от того же списка переменных и находящаяся в СКНФ относительно этого списка, что F1 выражает собой формулу F. Формула F1 определена однозначно с точностью до перестановки конъюнктивных членов. Опишем два способа приведения к совершенным нормальным формам. 1-й способ – аналитический Приведение к СКНФ. Алгоритм приведения. 1. привести формулу с помощью равносильных преобразований к КНФ. 2. удалить члены конъюнкции, содержащие переменную вместе с ее отрицанием (если такие окажутся); 3. из одинаковых членов конъюнкции (если такие окажутся) удалить все, кроме одного; 4. из одинаковых членов каждой дизъюнкции (если такие окажутся) удалить все, кроме одного; 5. если в какой-нибудь дизъюнкции не содержится переменной xi из числа переменных, входящих в исходную формулу, добавить к этой дизъюнкции член 6. если в полученной конъюнкции окажутся одинаковые члены, воспользоваться предписанием из п. 3. Полученная формула и является СКНФ данной формулы.
Привести следующие формулы к СКНФ с помощью равносильных преобразований: 1. 2. Решение. 1. 2.
2-й способ – табличный. Составляем таблицу истинности для данной функции. Рассматриваем только те строки таблицы, где формула принимает значение 0. Каждой такой строке соответствует дизъюнкция всех переменных (без повторений). Причем аргумент, принимающий значение 0, берется без отрицания, значение 1 – с отрицанием. Наконец, образуют конъюнкцию полученных дизъюнкций.
Построить СКНФ для данных формул логики высказываний. 1. 2. Решение. 1. Строим таблицу значений, используя предыдущий пример.
Рассматриваем только наборы, на которых формула принимает значение ноль. СКНФ (0): № 0, 1, 2, 3, 6:
2. Строим таблицу значений, используя предыдущий пример.
СКНФ (0): № 0, 1, 2:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.168.68 (0.006 с.) |

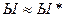 , к Ы* применим первый дистрибутивный закон необходимое число раз, тогда получим приведенную форму, которая будет являться ДНФ, если закон уже применить нельзя. Если невозможно применить первый дистрибутивный закон, то все члены любой конъюнкции в этой форме является либо переменными или отрицаниями переменных.
, к Ы* применим первый дистрибутивный закон необходимое число раз, тогда получим приведенную форму, которая будет являться ДНФ, если закон уже применить нельзя. Если невозможно применить первый дистрибутивный закон, то все члены любой конъюнкции в этой форме является либо переменными или отрицаниями переменных.
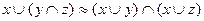
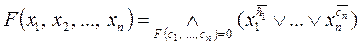 ,
,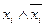 и применить закон дистрибутивности дизъюнкции относительно конъюнкции;
и применить закон дистрибутивности дизъюнкции относительно конъюнкции;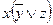 ;
;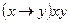 .
.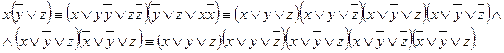

 .
.