
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7.5 Эйлеровы и гамильтоновы графы.Содержание книги
Поиск на нашем сайте
Классической в теории графов является следующая задача. В городе Кенигсберге имеется два острова, соединенных семью мостами с берегами реки Преголь и друг с другом так, как показано на рисунке.
Задача состоит в следующем: осуществить прогулку по городу таким образом, чтобы, пройдя по одному разу по каждому мосту, вернуться обратно. Решение этой задачи сводится к нахождению некоторого специального маршрута в графе. Пусть G – псевдограф. Цепь (цикл) в G называется эйлеровой (эйлеровым), если она (он) проходит по одному разу через каждое ребро псевдографа G. Поставим в соответствие схеме мультиграф G, изображенный на рисунке,
в котором каждой части суши соответствует вершина, а каждому мосту – ребро, соединяющее соответствующие вершины. На языке теории графов задача звучит следующим образом: найти эйлеров цикл в мультиграфе G. Граф является эйлеровым, если он содержит эйлеров цикл. Теорема. Связный граф является эйлеровым тогда и только тогда, когда каждая вершина имеет четную локальную степень. Теорема. Связный граф содержит эйлерову цепь тогда и только тогда, когда ровно две вершины имеют нечетную локальную степень. Рассмотрим алгоритм построения эйлеровой цепи в данном эйлеровом графе. Этот метод известен под названием алгоритма Флёри. Теорема. Пусть G – эйлеров граф; тогда следующая процедура всегда возможна и приводит к эйлеровой цепи графа G. Выходя из произвольной вершины и, идем по ребрам графа произвольным образом, соблюдая лишь следующие правила: · стираем ребра по мере их прохождения и стираем также изолированные вершины, которые при этом образуются; · на каждом этапе идем по мосту только тогда, когда нет других возможностей. Любой простой полный граф с нечетным количеством вершин является эйлеровым. Любой циклический граф является эйлеровым. Граф, являющийся колесом, не является эйлеровым. Критерий эйлеровости: Для того, чтобы граф являлся эйлеровым необходимо и достаточно, чтобы он был связным и все его вершины имели четную степень. Цепь (цикл) в G называется гамильтоновой (гамильтоновыми), если она (он) проходит по одному разу через каждую вершину псевдографа G. Граф является гамильтоновым, если он содержит гамильтонов цикл.
С понятием гамильтоновых циклов тесно связана так называемая задача коммивояжера: в нагруженном графе G определить гамильтонов цикл минимальной длины (иными словами, коммерсант должен совершить поездку по городам и вернуться обратно, побывав в каждом городе ровно один раз, и при этом стоимость такой поездки должна быть минимальной). Приведем теорему Дирака, которая отвечает на вопрос: существует ли в графе гамильтонов цикл. Теорема. Если в простом графе с n (³ 3) вершинами локальная степень каждой вершины не менее n/2, то граф является гамильтоновым. Любой простой полный граф является гамильтоновым. Любой циклический граф является гамильтоновым. Граф, являющийся колесом, является гамильтоновым. Критерии гамильтоновости: 1. любой полный граф является гамильтоновым 2. если в графе, кроме простого цикла, проходящего через все его вершины, содержатся и другие ребра, то граф является гамильтоновым. 3. если для любых двух вершин А и В графа с m вершинами выполняется: степень А + степень В ≤ m, то граф является гамильтоновым. 4. если граф с m вершинами и любая Лабораторная работа № 5 Эйлеровы графы Цель работы; 1) Рассмотреть понятия эйлеров путь, эйлеров цикл. 2) Дать определение эйлерова графа. 3) Рассмотреть свойства эйлеровых графов. Литература: 1) "Графы и их применение", Березина Л.Ю., М.: Просвещение, 1979г. 2) "Теория графов. Алгоритмический подход", Кристофидес Н. 3) "Применение теории графов в программировании", Евстигнеев В.А Наука, 1985г. Порядок выполнения работы: I Разработать схему алгоритмов основной программы и подпрограмм. II Написать и отладить программу на языке Turbo Pascal. Задание: Заданы графы: 1)
2)
3) 5)
Краткие теоретические сведения: Граф называется полным, если каждые две его вершины соединены одним и только одним ребром. Степенью вершины называется число ребер графа, которым принадлежит эта вершина.
Степ. А=1 Степ. В=2 Степ. С=2 Степ. D=l Степ. Е=0 Вершина называется нечетной, если её степень - число нечетное. Вершина называется четной, если её степень - число четное. Степень каждой вершины полного графа на единицу меньше числа его вершин.
Теорема о сумме степеней графа: В графе Г - сумма степеней всех его вершин, есть число четное, равное удвоенному числу его ребер, т.е.
где р - число ребер графа, п- число вершин. Содержание отчета: 1) Составление алгоритмов. 2) Написание программы на языке Turbo Pascal. 3) Отладка программы. Контрольные вопросы: 1) Что такое полный граф? 2) Дайте понятие степени вершины графа? 3) Какая вершина графа называется четной? 4) Какая вершина графа называется нечетной? 5) Сформулируйте теорему о сумме степеней вершин графа?
Тема 7.6 Плоские графы.
Граф называется плоским, если никакие два его соседних ребра не имеют других общих точек за исключением их общей вершины. Рисунок графа называется его плоским представлением, если на нем никакие два ребра не имеют общих точек пересечения, если не считать точкой пересечения их вершину. Теорема: Для того, чтобы граф являлся плоским необходимо и достаточно,чтобы существовало его плоское представление. В качестве характеристики плоского графа вводят понятие грань. Гранью в плоском представлении графа называется часть плоскости, ограниченная простым циклом и не имеющая внутри себя других циклов.
Грани: (2,4,5,6,2) (1,2,3,1) (1,7,4,1) (1,4,2,3,1) Границей грани называется простой цикл, ограничивающий грань. Две грани называются соседними, если их границы имеют хотя бы одно общее ребро. Существует так называемая бесконечная грань, т.е. часть плоскости, лежащая вне графа и ограниченная изнутри простым циклом
АВ называют перегородкой, и если у графа есть перегородка, то не существует бесконечной грани. Теорема: Если в плоском представлении графа без перегородок V – количество вершин, P – количество ребер, G – количество граней (с учетом бесконечной), то V – P + G = 2 (формула Эйлера). Данная теорема используется в задачах для того, чтобы доказать, что заданный граф не является плоским.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 252; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.181.102 (0.008 с.) |


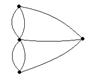
 степень больше либо равна m/2, то граф является гамильтоновым.
степень больше либо равна m/2, то граф является гамильтоновым.
 4)
4)


 Е
Е





