Раздел 7. Основы теории графов.

 

Тема 7.1 Понятие неориентированный граф. Основные определения.

 

Графом (Г) называется не пустое множество точек и множество отрезков, оба конца которых принадлежат данному множеству.

 

При изображении графа расположение точек, длина отрезков не играют роли, не имеют значения, более того не важно являются ли выбранные обрезки прямыми или кривыми.

Точки называются вершинами, отрезки – ребрами.

 

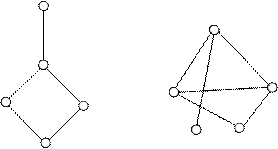
Вершина, не принадлежащая ни одному из ребер называется изолированной.

1.

2. n – количество вершин, p – количество ребер

1. n=4, p=6.

 

 

2. n=3, p=0.

 

 

3. n=5, p=2.

 

 

A

 

Теоремой называется необходимое и достаточное условие, что два рисунка изображают один и тот же граф.

Теорема: Для того, чтобы два рисунка изобразили один и тот же граф необходимо и достаточно, чтобы между вершинами на этих рисунках существовало такое взаимно-однозначное соответствие, при котором выполнялись бы два условия:

1. Две вершины графа на первом рисунке соединены ребром, когда соответствующие им вершина на втором рисунке соединены ребром.

2. Две вершины графа на втором рисунке соединены ребром, когда соответствующие им вершина на первом рисунке соединены ребром.

Графом Г называется не пустое множество М и множество отношений на нем.

Г=(M,Q)

Лабораторная работа № 1.

Основные характеристики графа

 

Цель работы:

1) Изучить понятия вершины, ребра и дуги графа, цикл графа.

2) Рассмотреть понятие дерево.

Литература:

1) "Графы и их применение", Березина Л.Ю., М: Просвещение, 1979г.

2) "Теория графов. Алгоритмический подход", Кристофидес Н.

3) "Применение теории графов в программировании", Евстигнеев В.А. - М.: Наука, 1985г.

Порядок выполнения работы:

I Разработать схему алгоритмов основной программы и подпрограмм.

II Написать и отладить программу на языке Turbo Pascal.

Задание:

Задача Прима-Краскала.

Дана плоская страна и в ней n-городов. Нужно соединить все города телефонной связью так, чтобы общая длина телефонных линий была минимальной.

Другими словами, дан граф с n-вершинами; длины рёбер заданы
матрицей { }, i,j=1,2,3,,n. Найти дерево минимальной длины.

Краткие теоретические сведения:

Граф представляет собой непустое множество точек и множество отрезков, оба конца которых принадлежат заданному множеству точек.

Ребро, ведущее из вершины в неё же, называется петлей.

Граф без кратных ребер и петель называется простым.

Цепью между вершинами u и v называется последовательность ребер, соединяющих u и v.

Связный граф - это граф, где существует цепь между любой парой вершин u и v; иногда такой граф называют односвязанным.

Циклом называется цепь из V в V.

Деревом называется граф без циклов.

Дерево с n -вершинами имеет n-1 ребер. Поэтому краткое описание поставленной задачи выглядит следующим образом: в цикле n-1 раз делай: Выбрать самое короткое ещё не выбранное ребро при условии, что оно не образует цикла с уже выбранными. Выбранные таким образом ребра образуют искомое дерево.

Кроме того, при проверки того, что новое ребро не образовывает цикла со старыми, используйте следующее: до построения дерена окрасим каждую вершину i в отличный от других цвет i. При выборе очередного ребра, скажем (i, j), где i и j имеют разные цвета, вершина j и все окрашенные в её цвет (т.е. ранее соединенные с ней) перекрашиваются в цвет i. Таким образом, выбор вершин разного цвета обеспечивает отсутствие циклов. После выбора n-1 ребер все вершины получают один цвет.

В заключении анализа алгоритма надо оценить требуемую память и требуемое число операций. С памятью здесь все ясно: в решении удобно хранить n-1 ребер ответа. Всего требуется память 0(n²), т.е. порядка ≈ , что учитывая реальные величины n, необременительно. Для нахождения текущего минимального ребра надо просмотреть 0() чисел и сделать это n-1 раз, так что временная сложность алгоритма 0(). Это тоже реально.

Содержание отчета;

1) Составление алгоритмов.

2) Написание программы на языке Turbo Pascal.

3) Отладка программы.

Контрольные вопросы:

1) Что такое граф?

2) Какой граф называется простым?

3) Что называется цепью?

4) Что такое цикл?

5) Понятие дерева.