
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Основы теории множествСтр 1 из 20Следующая ⇒
Раздел 1. ОСНОВЫ ТЕОРИИ МНОЖЕСТВ Тема 1.1 Основные понятия теории множеств.
Множеством называется совокупность каких-либо объектов, обладающим общим для всех характеристическим свойством. Это определение нельзя считать строгим, так как понятие множества является исходным понятием математики и не может быть определено через другие математические объекты. Один из основателей теории множеств Г. Кантор определял множество так: "Множество есть многое, мыслимое как целое". Множество – это неопределяемое понятие, которое задается перечислением предметов, входящих (составляющих) в него, либо их свойствами. Всякое множество состоит из элементов. Объекты, сущности или элементы, составляющие множество, обозначаются строчными латинскими буквами: a, b, m, x, y …; множество часто обозначают прописными латинскими буквами А, В, М, Х, У…. Знак Î обозначает вхождение или принадлежность; х Î Е читается: «элемент х принадлежит множеству Е», или короче: «х— элемент множества Е». Следует различать «общий элемент» х множества Е, т. е. произвольный элемент, характеризующийся единственным свойством «принадлежать множеству», и конкретные элементы а, b, c,..., каждый из которых отличен от остальных. Если х не принадлежит Е, будем писать х Ï Е, что читается «х не является элементом множества Е» или «х не принадлежит множеству Е». Если каждый элемент множества А является элементом множества В, говорят, что множество А является подмножеством множества В,и записывают А Í В или В Ê А. Отметим, что по определению само множество А является своим подмножеством, т.е. А Í А. Множество называется конечным, если оно одержит конечное число элементов. Все остальные множества называются бесконечными. Также необходимо выделить пустые множества. Множества, не содержащие элементы, называются пустыми. Принято считать, что пустое множество является подмножеством любого множества, Æ Í А, где А – любое множество. Таким образом, всякое множество содержит в качестве своих подмножеств пустое множество и само себя. Существует два способа задания множества: 1) перечисление элементов (только для конечных множеств):
2) указание свойств:
Пример: 1) 2) Мощностью множества М называется число элементов в него входящих.
Самостоятельная работа № 1 Тема 1.3 Свойства операций.
Операции над множествами обладают некоторыми свойствами. Эти свойства выражаются совокупностью тождеств, справедливых независимо от конкретного содержания входящих в них множеств. 1. транзитивность операции включения:
т.е. если множество А является подмножеством В, а множество В является подмножеством множества С, то множество А является подмножеством множества С. 2. дистрибутивность операции пересечения относительно объединения:
т.е. если множество А объединить с множеством В, а потом пересечь с множеством С, то это тоже самое, что А пересечь с С и В пересечь с С, а потом объединить их. 3. дистрибутивность операции объединения относительно пересечения:
т.е. если множество А пересечь с множеством В, а потом объединить с множеством С, то это тоже самое, что А объединить с С и В объединить с С, а потом пересечь их. 4. первый закон двойственности:
т.е. дополнение множества 5. второй закон двойственности:
т.е. дополнение множества 6. ассоциативность операции объединения:
7. ассоциативность операции пересечения:
8. свойства операции объединения: · коммутативность объединения:
· · · 9. свойства операции пересечения: · коммутативность пересечения:
· · · 10. свойства операции разности: · · · · · 11. дополнение к дополнению любого множества есть всегда само множество, т.е. 12. 13.
Тест 1. Будет ли пустое множество V каким-либо подмножеством некоторого множества? а) будет собственным подмножеством; б) будет несобственным подмножеством; в) не будет никаким подмножеством. 2. Что есть множество А\В, если А - множество всех книг в библиотеке МЭСИ по различным отделам науки и искусства, а В – множество всех книг во всех библиотеках России? а) множество математических книг в России без математических книг в МЭСИ;
б) множество книг по искусству в библиотеке МЭСИ; в) множество книг в библиотеке МЭСИ по искусству и науке, кроме математических. 3. Совпадают ли дистрибутивные законы Булевой алгебры и алгебры действительных чисел; а) оба совпадают; б) оба не совпадают; в) один совпадает, другой - нет. 4. Есть ли законы для дополнений в алгебре действительных чисел? а) да; б) нет; в) некоторые есть, некоторых нет. 5. Справедливы ли законы идемпотентности Булевой алгебры в алгебре действительных чисел? а) справедливы; б) несправедливы; в) один справедлив, другой нет. 6. Обладают ли свойством двойственности формулы поглощения? а) да; б) нет; в) одна обладает, другая нет. 7. Можно ли поставить в соответствие единицу или ноль соответственно универсальному и пустому множеству, исходя из свойств операций? а) можно; б) единицу - можно, ноль - нет; в) ноль - можно, единицу - нет. 8. Обладают ли формулы склеивания свойством двойственности а) нет; б) да; в) одна обладает, другая нет. 9. Будет ли каждое из множеств А, В, С, D подмножеством другого, если А - множество действительных чисел, В - множество рациональных чисел, С - множество целых чисел, D - множество натуральных чисел. а) да; б) нет; в) лишь некоторые из множеств являются подмножествами перечисленных множеств Контрольная работа 1 Вариант
1. А={х | х Определить количество подмножеств у множества А. Выписать все подмножества у множества В. 2. Х={ однозначные натуральные числа, кратные 3} Найти: Х 3. А=(-1,8]; В=[0,12] Найти: А\В, В\А, В\(А 4. Доказать: А 5. Упростить: (А
2 Вариант
1. А={х | x Определить количество подмножеств у множества А. Выписать все подмножества у множества В. 2. Х={ Однозначное натуральное число: 4} Найти: Х 3. А=[2,14]; В=(-3,10] Найти: А\В, В\А, В\(А 4. Доказать: 5. Упростить: (А
Раздел 2. ФОРМУЛЫ ЛОГИКИ. Тема 2.2 Формулы логики.
Алфавитом называется любой непустой набор символов. Элементы этого набора называются символами алфавита. Словом в алфавите Формула алгебры логики определяется следующим образом (индуктивное определение): · Любая логическая переменная есть формула. · Если · Если · Других формул нет. Подформулой формулы Для сокращения записи формул обычно принимаются следующие соглашения: · если часть формулы заключена в скобки, то сначала производится действие в скобках, · если над частью формулы стоит знак отрицания, то он заменяет собой скобки, в которые заключена эта часть формулы. Принят следующий порядок выполнения операций: · Отрицание · конъюнкция, · дизъюнкция, · импликация и эквивалентность в порядке их записи, Формула называется тождественно истинной или тавтологией, если она реализует функцию «тождественная единица», и тождественно ложной, если 0.
Являются ли формулы тождественно истинными:
Формулы логики, принимающие всегда ложное значение, называются тождественно ложными (или противоречиями). Например, формула Формулы алгебры логики, принимающие значение «ложь» хотя бы на одном наборе значений атомов, входящих в формулу называются опровержимыми. Формулы алгебры логики, принимающие значение «истина» хотя бы на одном наборе значений атомов, входящих в формулу называются выполнимыми. Формулы Р и Q называются равносильными, если их истинностные значения совпадают при любом выборе истинностных значений атомов, входящих в эти формулы. Запись Р Самостоятельная работа №2.
Тест 1. Следующее высказывание может быть интерпретировано как сложное высказывание: "Неверно, что первым пришел Петр или Павел". Каковы составляющие его элементарные высказывания? а) А: "Неверно, что первым пришел Петр"; В: "Неверно, что первым пришел Павел"; б) А: "Первым пришел Петр"; В: "Неверно, что первым пришел Павел"; в) А: "Первым пришел Петр"; В: "Первым пришел Павел". 2. Какой из формул может быть записано высказывание предыдущего вопроса? а) А ∨ В; б) А ∨ В; в) А ∧В. 3. Будет ли высказывание S=(А→В)∧(В→С)→(А→С): а) тождественно истинным; б) тождественно ложным; в) переменным. 4. В высказывании S: "Треугольники равны только тогда, когда равны их стороны". Равенство углов в треугольнике является: а) необходимым условием; б) достаточным условием; в) необходимым и достаточным условием.
Самостоятельная работа №3. Самостоятельная работа №4. Контрольная работа I вариант 1. Составить истинностную таблицу для ы:
2. Записать приведённую равносильную форму для ы: 3. Является ли заданная высказывательная форма тавтологией: 4. Составить ДНФ и КНФ для ы: 5. Упростить: 6. Выразить заданную функцию F из алгебраического высказывания через F1(x)= x; F2(x,y)=x F=(x∧y∧z)∨(x→y)
II вариант 1. Составить истинностную таблицу для ы: 2. Записать приведённую равносильную форму для ы: 3. Является ли заданная высказывательная форма тавтологией: 4. Составить ДНФ и КНФ для ы: 5. Упростить: 6. Выразить заданную функцию F из алгебраического высказывания через F1(x)= x; F2(x,y)=x
F=(y→x)∧(x∨y∨z)
Раздел 3. БУЛЕВЫ ФУНКЦИИ.
Самостоятельная работа №5. Тема 3.3 Минимальная ДНФ.
Уже известно, что произвольная булева функция может быть представлена формулой в дизъюнктивной и конъюнктивной нормальной форме. Равносильными преобразованиями можно получить формулу, содержащую меньшее, чем исходная, число переменных. Минимальной ДНФ (МДНФ) функции f(x1, x2, …, xn) называется ДНФ, реализующая функцию f и содержащая минимальное число символов переменных по сравнению со всеми другими ДНФ, реализующими функцию f. Минимальную ДНФ данной формулы можно найти, перебрав конечное число равносильных ей ДНФ и выбрав среди них ту, которая содержит минимальное число переменных. Однако при большом числе переменных такой перебор практически невыполним. Существуют эффективные способы нахождения минимальной ДНФ. Рассмотрим два из них. Каждый из рассмотренных ниже методов состоит из двух этапов: · построение сокращенной ДНФ; · построение матрицы покрытий. Построение МДНФ. Если для всякого набора а = (а1, а2, …, an) значений переменных условие g(a)=1 влечет f(a)=1, то функция g называется частью функции f (или функция f накрывает функцию g). Если при этом для некоторого набора с = (с1, с2, …, сn)функция g(c)=1, то говорят, что функция g накрывает единицу функции f на наборе с (или что g накрывает конституенту единицы Конституента единицы функции f есть часть функции f, накрывающая единственную единицу функции f. Элементарная конъюнкция К называется импликантом функции f, если для всякого набора а = (а1, а2, …, an) из 0 и 1 условие К(а)=1 влечет f(a)=1. Определение. Импликант К функции f называется простым, если выражение, получающееся из него выбрасыванием любых множителей, уже не импликант функции f. Всякий импликант функции f есть часть функции f. Теорема. Всякая функция реализуется дизъюнкцией всех своих простых импликант. Сокращенная ДНФ функции f есть дизъюнкция всех простых импликант функции f. Всякая функция f реализуется своей сокращенной ДНФ. Для всякой функции, не равной тождественно нулю, существует единственная сокращенная ДНФ. Минимизация формул алгебры логики на кубе. Рассмотрим проблему минимизации для геометрического способа задания формул алгебры логики на кубе.
Каждый геометрический элемент меньшей размерности покрывается геометрическими элементами большей размерности. Каждая конъюнкция большего ранга покрывается всеми конъюнкциями меньшего ранга. Геометрические эквиваленты называют интервалами. Интервал L-го ранга – подмножество вершин куба, соответствующих конъюнкции ранга L. Например: Kонъюнкции x соответствует 4 вершины: 100, 101, 110, 111.
На кубе отмечают вершины, где формула алгебры логики равна 1. Эти вершины образуют подмножество Т1. Для того, чтобы задать ДНФ на кубе, необходимо задать покрытие всех вершин.
Например: Пусть есть функция, которая равна 1 в отмеченных точках.
J1 и J3 – максимальные интервалы, J2 – не является максимальным
где ri – ранги конъюнкции, образующих покрытие множества T1. Необходимо найти Т1, при котором R будет минимальным. Сокращенная ДНФ(СДНФ) – ДНФ, которая соответствует покрытию множества Т1 всеми максимальными интервалами. В данном примере СДНФ = Минимальная ДНФ получается из СДНФ путем выбрасывания из покрытия множества Т1 максимальными интервалами некоторых “лишних” интервалов.
Тема 3.4 Представление булевой функции в виде минимальной ДНФ. Самостоятельная работа №6. Самостоятельная работа №7 Задачи 1. Доказать, что пересечение любых двух замкнутых классов замкнуто. 2. Доказать, что объединение двух замкнутых классов не всегда замкнуто Тема 3.7 Теорема Поста.
Для того чтобы система функций была полной, необходимо и достаточно, чтобы она не содержалась целиком ни в одном из классов T 0, T 1, L, S, M. Доказательство. Докажем необходимость этого условия. Пусть система N = { f 1, f 2,... fs,...} полна в Р 2, покажем, что тогда она не лежит целиком в Q, где через Q обозначим любой из классов T 0, T 1, L, S, M. Докажем от противного, пусть N Í Q, очевидно, [ N ] Í [ Q ] = Q, но [ N ] = P 2, т.к. N – полна в Р 2, отсюда Р 2= Q, но это не так. Необходимость доказана. Докажем достаточность. Пусть F = { f 0, f 1, fL, fm, fs }, где f 0Ï T 0, f 1Ï T 1, fL Ï L, fs Ï S и fm Ï M. Покажем, что суперпозицией функций системы F можно получить полную систему G = { x 1& x 2, 1. Пусть g (x) = f 0(x, …, x). Тогда g (0) = f (0, …, 0) = 1. Далее возможны два случая: g (1) = 1. Тогда g (x) º 1. Функция h (x) = f 1(g (x), …, g (x)) = f 1(1, …, 1) = 0, т.е. h (x) º 0. Получили константы 0 и 1; g(1) = 0. Тогда g (x) = В обоих случаях получили обе константы. 2. По лемме о немонотонной функции суперпозицией над { fm, 0, 1} можно получить отрицание. 3. По лемме о нелинейной функции суперпозицией над { fL, 1, Следствие. Всякий замкнутый класс функций из Р 2, не совпадающий с Р 2 содержится, по крайней мере, в одном из замкнутых классов T 0, T 1, L, S, M. Действительно, если N не является подмножеством Q, то [ N ] = P 2, что неверно. Примеры использования теоремы Поста. 1. Покажем, что система функций { f 1 = x 1 x 2, f 2 =0, f 3 =1, f 4 = x 1Å x 2Å x 3} полна в Р 2. Составим таблицу, которая называется критериальной:
Из таблицы видно, что какой бы класс мы ни взяли, всегда есть функция из данной системы, которая в этот класс не входит. Можно сформулировать следующее правило: для того чтобы система функций была полна, необходимо и достаточно, чтобы в каждом столбце критериальной таблицы был хотя бы один «минус». Отметим еще одно обстоятельство, касающееся приведенной системы. Какую бы функцию из этой системы мы ни удалили, система станет неполной, действительно, { f 2, f 3, f 4}Ì L, { f 1, f 3, f 4}Ì T 1, { f 1, f 2, f 4}Ì T 0, { f 1, f 2, f 3}Ì M. 2. Мы знаем, что система { x 1| x 2} – полна в Р 2. Какова для нее критериальная таблица? x 1| x 2=
3. Составим критериальную таблицу для другой полной системы функций из Р2: {0, 1, x 1 x 2, x 1Å x 2}.
Согласно критериальной таблице, полной является и система {1, x 1 x 2, x 1Å x 2}. Константа 0 введена в эту систему для удобства, тогда мы можем записать полином Жегалкина в виде, где а 4. Выясним, полна ли система
и А – полная система функций. Система функций { f 1,..., fs,...} называется базисом в Р 2,если она полна в Р 2, но любая ее подсистема не будет полной. Например, система функций { x 1& x 2, 0, 1, x 1
Контрольная работа Вариант I 1. Составить таблицу истинности для булевой функции:
2. Составить СДНФ и СКНФ для:
3. Найти минимальную (сокращённую) ДНФ для в.ф. ы
4. Определить является ли следующая система функций полной {0,1,x, 5. Дана формула
Вариант II 1. Составить таблицу истинности для булевой функции:
2. Составить СДНФ и СКНФ для:
3. Найти минимальную (сокращённую) ДНФ для в.ф. ы
4. Определить является ли следующая система функций полной
5. Дана формула Самостоятельная работа №8. Квантор существования Операцией связывания квантором существования называется правило, по которому каждому одноместному предикату Р(х), определенному на множестве М, сопоставляется высказывание, обозначаемое
Словесным аналогом квантору существования $ является: «существует», «найдется» и т.п. Подобно выражению Если одноместный предикат Р(х) задан на конечном множестве М = {a1, a2, …, an}, то высказывание Пример. Пусть Р(х) – предикат «х – четное число», определенный на множестве N. Дать словесную формулировку высказыванию Решение. Исходный предикат Р(х): «х – четное число» является переменным высказыванием: при подстановке конкретного числа вместо переменной х он превращается в простое высказывание, являющееся истинным или ложным, например при подстановке числа 5 – ложным, при подстановке числа 10 – истинным. Высказывание Операцией связывания квантором существования по переменной х1 называется правило, по которому каждому n-местному (n ³ 2) предикату Р(х1, х2, …, хn), определенному на множествах М1, М2, …, Мn, сопоставляется новый (n-1)-местный предикат, обозначаемый
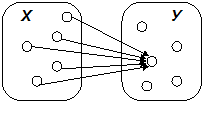
Выше уже было сказано, что переменная, на которую навешен квантор, называется связанной, несвязанная квантором переменная называется свободной. Выражение, на которое навешивается квантор, называется областью действия квантора и все вхождения переменной, на которую навешен квантор, в это выражение являются связанными. На многоместные предикаты можно на разные переменные навешивать различные кванторы, нельзя на одну и ту же переменную навешивать сразу два квантора. Пример. Пусть предикат Р(х, у) описывает отношение «х любит у» на множестве людей. Рассмотреть все варианты навешивания кванторов на обе переменные. Дать словесную интерпретацию полученных высказываний. Решение. Обозначим предикат «х любит у» через ЛЮБИТ(х, у). Предложения, соответствующие различным вариантам навешивания кванторов, проиллюстрированы на рисунках, где х и у показаны на разных множествах, что является условностью и предпринято только для объяснения смысла предложений (реальные множества переменных х и у, очевидно, должны совпадать): 1.
2.
3.
4.
5.
6.
Из приведенного выше примера можно сделать вывод о том, что перестановка кванторов общности и существования меняет смысл высказывания, т.е. кванторы общности и существования не обладают в общем случае свойством коммутативности. Итак, одноименные кванторы можно менять местами, разноименные кванторы менять местами нельзя.
Самостоятельная работа №9. Самостоятельная работа №10. Контрольная работа
Вариант 1
Первый уровень сложности – задачи №№ 1,2,3 – оценка “удовлетворительно” Второй уровень сложности – любые четыре задачи – оценка “хорошо” Третий уровень сложности – все задачи – оценка “отлично”
1. Найти области истинности следующих предикатов: а). « б). « в). « 2. Дана формула 3. Высказывательная форма x+y=z, с переменными, упорядоченными по алфавиту и принимающими значения из множества однозначных натуральных чисел, задаёт предикат F(x,y,z). Выпишите тройки чисел, компоненты которых находятся в отношении F. 4. Задано бинарное отношение 5. Пусть бинарные отношения P и S определены на М, где М-множество всех людей следующим образом: P= {(x,y) | x,y M,x является отцом y} S= {(x,y) | x,y M,x - дочь y} Описать явно следующие отношения: а). PS b)
Вариант 2
Первый уровень сложности – задачи №№ 1,2,3 – оценка “удовлетворительно” Второй уровень сложности – любые четыре задачи – оценка “хорошо” Третий уровень сложности – все задачи – оценка “отлично”
1. Найти области истинности следующих предикатов: а). « б). «
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.149.242 (0.261 с.) |

 - Множество М состоит из таких элементов х, обладающих свойством Р.
- Множество М состоит из таких элементов х, обладающих свойством Р. - перечисление;
- перечисление;
 ,
,  , где М2 – множество, Н2 – мощность множества;
, где М2 – множество, Н2 – мощность множества;


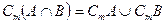
 , есть не что иное, как объединение дополнения множества А и дополнения множества В.
, есть не что иное, как объединение дополнения множества А и дополнения множества В.
 , есть пересечение их дополнений.
, есть пересечение их дополнений.

 ,
, ,
, ,
, .
.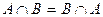 ,
,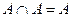 ,
, ,
, .
. ,
, ,
, ,
, ,
, .
.


 N: х-однозначное, составное число}
N: х-однозначное, составное число} Y, X
Y, X  Y, X\Y, Y\X
Y, X\Y, Y\X (В\С)=(А
(В\С)=(А  )U (
)U ( В)
В)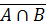 =
=  U
U 
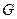 называется произвольная конечная (возможно пустая) последовательность символов из
называется произвольная конечная (возможно пустая) последовательность символов из 
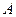 - формула, то
- формула, то 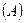 - формула (допустимы технические символы)
- формула (допустимы технические символы) – формулы, то
– формулы, то  – тоже формулы (допустимы все логические связки).
– тоже формулы (допустимы все логические связки).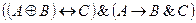
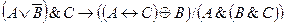

 - противоречие.
- противоречие. Q означает, что формулы Р и Q равносильны
Q означает, что формулы Р и Q равносильны

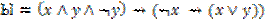


 y; F3(x,y)=x
y; F3(x,y)=x 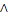 y
y




 функции f).
функции f). Сопоставим различным геометрическим элементам куба (вершинам, ребрам, граням и кубу) конъюнкции различных рангов. Сумма размерности геометрического эквивалента и ранга конъюнкции, ему соответствующей равна числу аргументов формулы алгебры логики.
Сопоставим различным геометрическим элементам куба (вершинам, ребрам, граням и кубу) конъюнкции различных рангов. Сумма размерности геометрического эквивалента и ранга конъюнкции, ему соответствующей равна числу аргументов формулы алгебры логики.
 .
.

 .
. }.
}. } можно получить конъюнкцию. Теорема доказана.
} можно получить конъюнкцию. Теорема доказана. = x 1 x 2Å1.
= x 1 x 2Å1. равны 0, если члены х
равны 0, если члены х  х
х  ... х
... х  , в полиноме отсутствуют.
, в полиноме отсутствуют. . Составим критериальную таблицу, очевидно
. Составим критериальную таблицу, очевидно  . Чтобы показать, что
. Чтобы показать, что 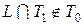 , достаточно найти одну функцию
, достаточно найти одну функцию 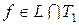 и
и  . Возьмем
. Возьмем  , удовлетворяющую требуемым условиям. Если f
, удовлетворяющую требуемым условиям. Если f  S \ T 0, то f (0,..., 0) = 1, f (1,..., 1)=0, следовательно, f
S \ T 0, то f (0,..., 0) = 1, f (1,..., 1)=0, следовательно, f 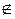 M, f
M, f  x 2 x 3
x 2 x 3  T 1
T 1


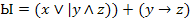
 }
}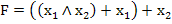 . Определите булевую функцию, которую реализует данная формула (составить таблицу истинности)
. Определите булевую функцию, которую реализует данная формула (составить таблицу истинности)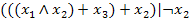

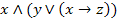

 . Определите булевую функцию, которую реализует данная формула (составить таблицу истинности)
. Определите булевую функцию, которую реализует данная формула (составить таблицу истинности) , которое ложно в том и только в том случае, когда предикат Р(х) тождественно ложен, и истинно в противном случае, то есть
, которое ложно в том и только в том случае, когда предикат Р(х) тождественно ложен, и истинно в противном случае, то есть
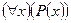 , в выражении
, в выражении  , который для любых предметов
, который для любых предметов  , превращается в высказывание
, превращается в высказывание  , ложное в том и только в том случае, когда одноместный предикат
, ложное в том и только в том случае, когда одноместный предикат  , определенный на множестве М1, тождественно ложен, и истинное в противном случае, то есть:
, определенный на множестве М1, тождественно ложен, и истинное в противном случае, то есть:











 на множестве действительных чисел R»
на множестве действительных чисел R» на множестве действительных чисел R»
на множестве действительных чисел R»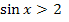 на множестве действительных чисел»
на множестве действительных чисел» . Являются ли вхождения переменной x свободными?
. Являются ли вхождения переменной x свободными? . Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность).
. Определите свойства заданного бинарного отношения (рефлексивность, симметричность, антисимметричность и транзитивность). c).
c).  d)
d) 
 x,y
x,y 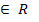 - множество действительных чисел»
- множество действительных чисел» на множестве действительных чисел R»
на множестве действительных чисел R»


