
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6.1 Принцип метода математической индукции.Содержание книги
Поиск на нашем сайте
Индукцией называется метод ведущий от частных примеров к некоторому общему выводу. Будем складывать нечетные числа:
Гипотеза может быть либо истинной, либо ложной - это доказывается методом математической индукции, то есть заключается в следующем: 1. Проверить: А(n) - гипотеза При n=1 – гипотеза выполняется: А(1) – верно. 2. Допустим, что при n=k, А(k) – верно. Взять n=k+1 и доказать, что А(k+1) – верно, используя пункт 2. Замечание. Чтобы показать, что эта формулировка следует из предыдущей, достаточно рассмотреть множество A={x Для доказательства в обратную сторону, множеству A О доказательствах, основанных на аксиоме индукции, говорят, что они проведены методом математической индукции. Такие доказательства имеют следующую структуру: - устанавливается справедливость P для n=0 (посылка индукции); - предполагается, что P справедливо для некоторого произвольного, но фиксированного n=k (индуктивное предположение); - доказывается, что из индуктивного предположения, следует, что P верно для n=k+1 (индуктивный шаг). Примеры.Проведем два доказательства методом математической индукции. 1) Сумма первых натуральных чисел от 0 до n включительно равна 0,5n(n+1): 0+1+…+n = 0,5n(n+1). Доказательство. Утверждение верно при n=0: имеем 0=0,5⋅0⋅(0+1) (посылка индукции). Предположим, что доказываемое утверждение верно для n=k (индуктивное предположение), то есть 0+1+…+k = 0,5k(k+1). Покажем, что тогда оно верно и для n=k+1, то есть 0+1+…+k+(k+1) = 0,5(k+1)(k+2) (индуктивный шаг). Сумма во втором равенстве отличается от суммы из первого равенства слагаемым k+1. Поэтому, в силу индуктивного предположения, получаем 0+1+…+k+(k+1) = 0,5k(k+1)+k+1 = 0,5(k+1)(k+2), что и требовалось доказать. В соответствии с принципом математической индукции, доказываемое утверждение верно для всех n. 2) Число подмножеств множества, содержащего n элементов, равно 2n. Доказательство. Утверждение верно при n=0: пустое множество ∅ (единственное множество, содержащее 0 элементов) имеет ровно одно подмножество ∅. Предположим теперь, что всякое множество с n=k элементами имеет 2k подмножеств, и покажем, что множество с n=k+1 элементами имеет 2k+1 подмножеств. Пусть A – произвольное множество с n=k+1 элементами. Так как k+1>0, то A не пусто и содержит хотя бы один элемент. Пусть a U={X⊂A | a∈X}; V={Y⊂A | a∉Y}. Положим A’=A\{a}. Множество A’ содержит k элементов, так что по индуктивному предположению, число его подмножеств равно 2k. Но подмножества множества A’ – это в точности подмножества множества A, не содержащие a. Следовательно, |V|=2k. Пара взаимно обратных отображений U→V, X→X\{a} и V→U, Y→Y∪{a} устанавливает между U и V взаимно однозначное соответствие, так что |U|=|V|=2k. Поэтому общее число подмножеств множества A составляет |U|+|V|=2k +2k =2k+1, что и требовалось доказать. Иногда принцип полной индукции применяется в следующей форме. Пусть P – утверждение относительно натуральных чисел n такое, что 1) P верно для n=n0; 2) из справедливости P(n) для n= n0, n0+1, …, n0+k следует справедливость P(n) для n= n0+k+1. Тогда P верно для всех n≥ n0. Принцип полной индукции в этой форме может быть сведен к предыдущей формулировке заменой утверждения P утверждением P’: утверждение P имеет место для всех t, таких, что n0≤t≤n. Возможны и другие модификации принципа полной индукции Теорема. Всякое непустое подмножество натурального ряда содержит наименьший элемент. Доказательство. Пусть A
|
||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.185.250 (0.005 с.) |

 - называется гипотезой (или предположением).
- называется гипотезой (или предположением). N | P верно для x}.
N | P верно для x}. N можно сопоставить свойство P «быть элементом множества A».
N можно сопоставить свойство P «быть элементом множества A».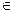 A. Разобьем совокупность всех подмножеств множества A на два класса. В класс U входят все подмножества, содержащие a, в класс V входят все подмножества, не содержащие a:
A. Разобьем совокупность всех подмножеств множества A на два класса. В класс U входят все подмножества, содержащие a, в класс V входят все подмножества, не содержащие a: A’, то и k+1
A’, то и k+1 


